
in chapter 6. 5.1 W developed over the years,and comprehensive literature surveys have are also used in the literature.Many analytical approaches have been terms"structure-property relationships"and"effective modulus theories" terms of constituent material properties is called"micromechanics."The ites literature,however,the analysis of effective composite properties in "minimechanics"[1].In the present context,and in much of the compos- of composites at the constituent material level should be referred to as to as "macromechanics,"it has been suggested that,perhaps,mechanics the behavior of composite material structures such as laminates is referred of mechanical behavior at the level of molecular or crystal structures.Since "micromechanics."To a materials scientist,the term may imply the study Before proceeding further,it is appropriate to discuss briefly the term of discontinuous fiber composites,including nanocomposites,is covered will be presented in chapter 4 and chapter 5,respectively.Micromechanics responding models for predicting strength and hygrothermal properties tents,and geometric arrangements of the fiber and matrix materials.Cor- in terms of the corresponding material properties,relative volume con- for predicting the effective moduli of continuous fiber-reinforced laminae detail.In this chapter,we will discuss various micromechanical models ever,and the roles of lamina constituent materials were not examined in stress-strain relationships involving the lamina effective moduli,how- concerned with the development and manipulation of macromechanical moduli of an equivalent homogeneous material.Chapter 2 was primarily aged stresses can be related to the volume-averaged strains by the effective volume element(RVE)in a heterogeneous composite,the volume-aver- relationships for composite materials.Recall that for some representative to be essential to the development of practical engineering stress-strain In the previous chapter,the concept of an effective modulus was found Introduction Fiber-Reinforced Lamina Effective Moduli of a Continuous

here. work." 图 and Halpin [4]. ships between volume fractions and weight fractions will be presented on weight fractions.Measurements are discussed later,but the relation- constituent volume fractions,but actual measurements are often based uent materials.We will find that the micromechanics equations involve ization of the relative volume or weight contents of the various constit- One of the key elements in micromechanical analysis is the character- are both essential if we are to understand better "how composites cations,micromechanical analysis and experimental characterization design the material as well as the structure.Aside from design impli- can become part of a powerful design methodology that enables us to to be sufficiently accurate by comparison with experiment,however,it of direct measurement.Once a micromechanical model has been shown chanical model and other measured properties because of the difficulty such as fiber transverse moduli are usually inferred from the microme- validity of the models.Indeed,as we will see later,some properties corresponding composite properties are required in order to assess the erties are required as input to the models,and similar data on the characterization.Experimental data on the constituent material prop- in such an approach and that there is no substitute for experimental question.On the other hand,experience has shown that there are pitfalls binations without actually fabricating and testing the composites in "What if?"questions regarding the effects of various fiber/matrix com- Ideally,micromechanical models should enable us to answer quickly complete set of simple lamina design equations. used along with the mechanics of materials equations to formulate a solutions or experimental data,and some of these equations are often involves empirical solutions that are based on curve-fitting to elasticity ciently accurate that they are often used in design.A third category violate some of the laws of elasticity theory,some of the results are suffi- the simplifying assumptions used in the mechanics of materials approach because of the complex geometries and boundary conditions.Although approach often involves numerical solutions of the governing equations level,and fiber-packing geometry is taken into account.The elasticity involves the solution for actual stresses and strains at the micromechanical packing geometry is generally arbitrary.The theory of elasticity models stress and strain distributions at the micromechanical level,and fiber- simplifying assumptions make it unnecessary to specify the details of the rials or the elasticity theory.In the mechanics of materials approach Micromechanical analyses are based on either the mechanics of mate- been published by Chamis and Sendeckyj [2],Christensen [3],Hashin [1] Principles of Composite Material Mechanics 登 we get the "rule of mixtures": Pe =PrUr+PmUm equation(3.3)and equation(3.4)and solving for the composite density, tuting the product of density and volume for weight in each term of tively.Note that the weight of the voids has been neglected here.Substi- the weights of the ith constituent,fibers,matrix,and composite,respec- where w:=Wi/Wo wr=Wi/Wo wm =Wm/Wo and Wi Ws,Wm,and W.are 8+8 voids,respectively.The corresponding equations for weight fractions are where vs vm,and vu are the volume fractions of the fiber,matrix,and Vr+Vm +Vo=1 In many cases this equation reduces to where v;=Vi/Ve=volume fraction of the ith constituent,Vi=volume of the ith constituent,V=total volume of the composite. volume fractions must be unity: For any number of constituent materials,n,the sum of the constituent Effective Moduli of a Continuous Fiber-Reinforced Lamina 8 罗 8 8 巴

FIGURE 3.1 0F566. 置 Representative area elements for idealized square and triangular fibe fractions.Indeed,optical determination of area fractions is possible from the fiber length,then the area fractions must be equal to the volume as the square and triangular arrays shown in figure 3.1.If we assume representative area elements for idealized fiber-packing geometries such tions that may be expected in fiber composites,it is useful to consider the composite during the cure cycle can cause void contents of the order range 0.1 to 1%.Without vacuum bagging,however,volatiles trapped in can be rearranged as v.-1-(W/pi)+(W.-W)/pm calculated from measured weights and densities: and composite,respectively.Similarly,equation(3.1)and equation (3.2) where piPepm and pe are the densities of the ith constituent,fiber,matrix, er-packing geometries. that the fiber spacing,s,and the fiber diameter,d,do not change along In order to get some idea as to the range of constituent volume frac- Typical autoclave-cured composites may have void fractions in the Equation (3.2)can also be rearranged so that the void fraction can be Principles of Composite Material Mechanics 思 In this case, used to describe the relationshin hetween the fiher area as shown in figure 3.3(b)and figure 3.3(c),then equation(3.10)can be we can approximate the Voronoi cell in figure 3.3(a)as an equivalent square closer to the center of that fiber than it is to the center of any other fiber.If [6].Each point within the space of a Voronoi cell for a particular fiber is cell(fig.3.3)and a statistical distribution describing the Voronoi cell size as the one shown in figure 3.2 can be quantified by the use of the Voronoi The random nature of the fiber-packing geometry in real composites such predictions to be exact. one piece of material to another,we should not expect our micromechanics of fibers.Since fiber-packing geometry is never entirely repeatable from be controlled for proper flow during molding)and the random orientation processing limitations(e.g.,the viscosity of the fiber/resin mixture must fiber composites,fiber volume fractions are usually much lower due to figure 3.2,and the fiber volume fractions range from 0.5 to 0.8.In short composites,the fibers are packed in a random fashion as shown in is generally not achievable in practice,however.In most continuous fiber The close packing of fibers required to produce these theoretical limits -0.000 and when s=d,the maximum fiber volume fraction is A similar calculation for the triangular array shows that Clearly,the maximum theoretical fiber volume fraction occurs when s=d. of the shaded square [5]: dividing the area of fiber enclosed in the shaded square by the total area micrographs.The fiber volume fraction for the square array is found by Effective Moduli ofa Continuous Fiber-Reinforced Lamina e13 8.12 c.10
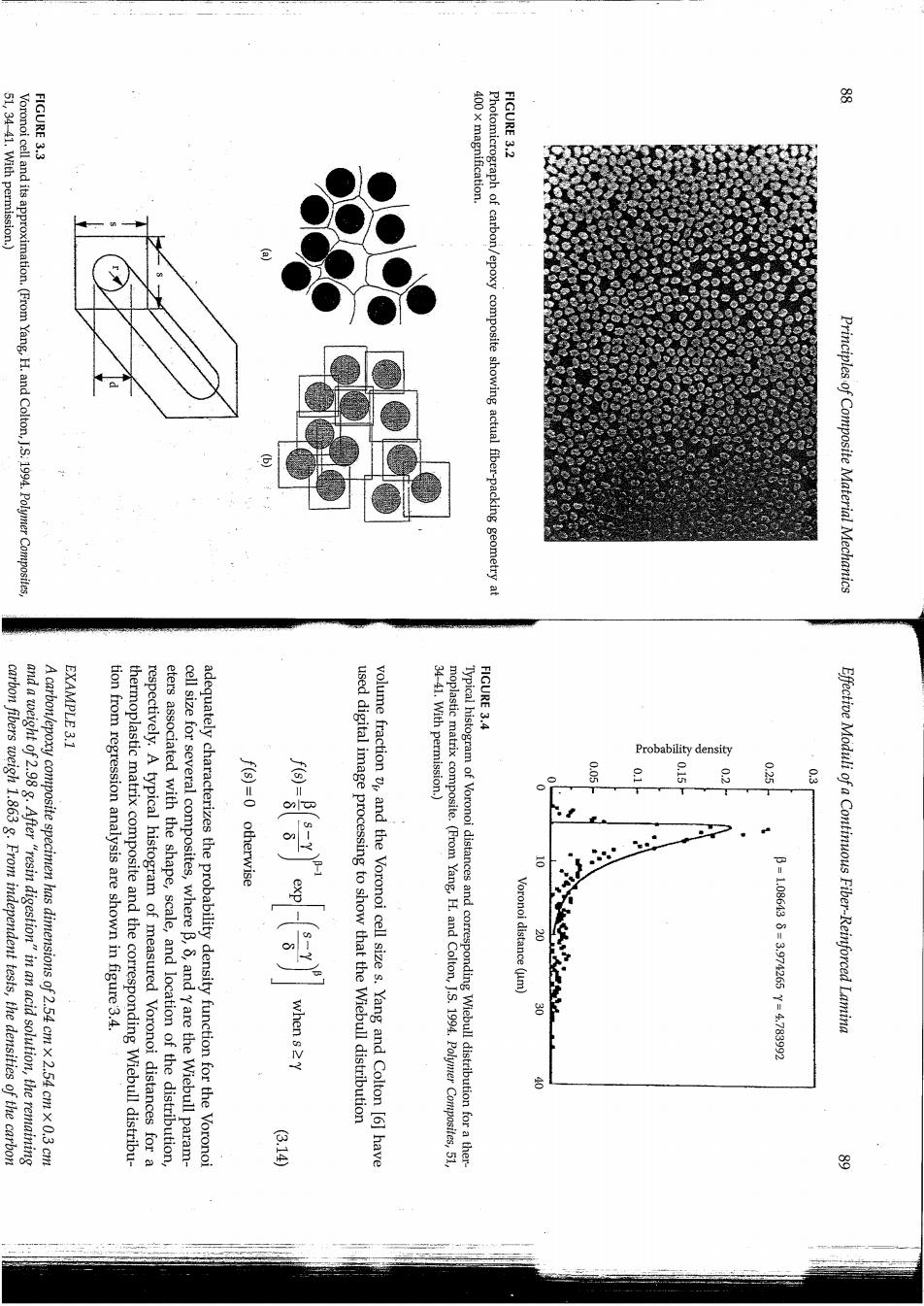
51,34-41.With permission.) FIGURE 3.3 400 x magnification FIGURE 3.2 Voronoi cell and its approximation.(From Yang,H.and Colton,J.S.1994.Polymer Composites Photomicrograph of carbon/epoxy composite showing actual fiber-packing geometry at Principles of Composite Material Mechanics EXAMPLE 3.1 FIGURE 3.4 Probability density carbon fibers weigh 1.863 g.From independent tests,the densities of the carbon and a weight of 2.98 g.After "resin digestion"in an acid solution,the remaining A carbon/epoxy composite specimen has dimensions of 2.54 cmx 2.54 cmx 0.3 cm tion from regression analysis are shown in figure 3.4. thermoplastic matrix composite and the corresponding Wiebull distribu- respectively.A typical histogram of measured Voronoi distances for a eters associated with the shape,scale,and location of the distribution, cell size for several composites,where B,5,and Y are the Wiebull param- adequately characterizes the probability density function for the Voronoi f(s)=0 otherwise when s 2Y used digital image processing to show that the Wiebull distribution volume fraction vp,and the Voronoi cell size s.Yang and Colton [6]have 34-41.With permission.) moplastic matrix composite.(From Yang,H.and Colton,J.S.1994.Polymer Composites,51 Typical histogram of Voronoi distances and corresponding Wiebull distribution for a ther 205 2 Voronoi distance (um) B10861393974265716783992 Effective Moduli of a Continuous Fiber-Reinforced Lamina 是 8

the sizing? EXAMPLE 3.2 The thickness is then t=(d.-d)/2=0.0000615 in(0.00156 mm) V40.506 (.0.00063in (00156 mm) diameter,do can be found from equation (3.10): Solution.The fiber spacing,s,which must be equal to the coated fiber be packed together in the tightest possible square array,what is the thickness of have a diameter d=0.0005 in (0.0127 mm)and the coated fibers are assumed to fibers and matrix together to form a unidirectional composite.If the bare fibers uniformly coated with an epoxy "sizing"of thickness t before bonding of the Assume that the carbon fibers in the specimen from example 3.1 have been and the matrix volume fraction is Therefore,the fiber volume fraction is Then,from equation (3.6), From equation(3.2) 10-0988-0.506-04320748.22% 15-0.5060750699 1.54-190541.20988-2V 5+00-1-00-1.0-00122-0288 u-1-0Ma/1gte%/0.809y12-00m0g1308 2.9871.54 From equation (3.9),the void fraction is P.(2.54)(2.54)0.3)cm Solution.The composite density is 2018 F1.548/cma Determine the volume fractions of fibers,epoxy matrix,and voids in the specimen. fibers and epoxy matrix materials are found to be 1.9 and 1.2 g/cm3,respectively. Principles of Composite Material Mechanics FIGURE 3.5 RVE and simple stress states used in elementary mechanics of materials models. Matrix Fiber Matrix (d)In-plane shear stress fiber-packing geometry,will be discussed later. (c)Transverse normal stress (b)Longitudinal normal stress (a)Representative volume element A=matrix area Ar=fber area A=total area More sophisticated mechanics of materials models,which do consider sisting of fiber material bonded to matrix material,as shown in figure 3.5 is not specified,so that the RVE may be a generic composite block con- materials approach to micromechanical modeling,fiber-packing geometry tropic continuous fiber-reinforced lamina.In the elementary mechanics of rials models for predicting four independent effective moduli of an ortho- The objective of this section is to present elementary mechanics of mate- Elementary Mechanics of Materials Models Effective Moduli of a Continuous Fiber-Reinforced Lamina

9 derivations force on the element must equal the sum of the forces acting on the fiber tudinal modulus,E1.Static equilibrium requires that the total resultant as shown in figure 3.5(b),the response is governed by the effective longi- If the RVE in figure 3.5(a)is subjected to a longitudinal normal stress,e 3.2.1 Longitudinal Modulus ters will be identified by using subscripts as defined in the following posite lamina,the fiber,or the matrix,and the corresponding parame- The volume averaging(or area averaging)may occur over the com- which loading is applied. 8=displacement,V=volume,and A=area associated with the face on where the overbar denotes an averaged quantity,and o=stress,g=strain, E-Jedv-iJedA do not change along the length,we can just use area averages: assumed that the stresses,strains,displacements,and RVE dimensions the corresponding volume-averaged quantities.Finally,since it is the stresses,strains,and displacements at each point,we only deal with the mechanics of materials approach does not require the specification of strains in the RVE that has been subjected to a simple state of stress.Since or compatibility relationships and assumptions about either stresses or Micromechanics equations will be developed from either equilibrium elastic,and orthotropic. RVE,the lamina is assumed to be macroscopically homogeneous,linearly fiber can be either isotropic or orthotropic.Following the concept of the elastic and homogeneous.The matrix is assumed to be isotropic,but the matrix materials.The fiber and matrix materials are assumed to be linearly ing at the interface is assumed,so that no slip occurs between fiber and element,the area fractions must equal the volume fractions.Perfect bond- parallel and that the dimensions do not change along the length of the as those in the actual composite.Since it is assumed that the fibers remain The constituent volume fractions in the RVE are assumed to be the same Principles of Composite Material Mechanics e.10 910 3.15 approach. 8·150We8et leading to this equation will now be examined by using a strain energy and is a useful design equation.The validity of the key assumptions equation (3.23)agrees well with experimental data from ref.[7](fig.3.6[bl) fiber volume fraction,as shown in figure 3.6.Although simple in form, This equation predicts a linear variation of the longitudinal modulus with mixtures for the longitudinal modulus: Substitution of equation(3.22)in equation(3.21)then yields the rule of strains in the composite,fiber,and matrix along the 1 direction are equal: Finally,the key assumption is that,due to perfect bonding the average modulus,Em does not need a second subscript. to let En =Er.Since the matrix is assumed to be isotropic,the matrix boron are practically isotropic.For the isotropic case,it is a simple matter carbon and aramid fibers exhibit orthotropic behavior,whereas glass and not necessarily equal to the transverse fiber modulus,En2.For example, assumed to be orthotropic.That is,the longitudinal fiber modulus,En,is Double subscripts are used for the fiber modulus since the fiber is and equation (3.19)becomes strains are neglected), EEe=ErEn Ur+EmEmIvm orthotropic,and that all materials follow a 1-D Hooke's law (i.e.,Poisson Under the assumptions that the matrix is isotropic,that the fiber is Ge=Gnvr+miVm rearranged to give a"rule of mixtures"for longitudinal stress: are equal to the corresponding volume fractions,equation (3.18)can be tively,and the second subscript refers to the direction.Since area fractions where subscripts c,f,and m refer to composite,fiber,and matrix,respec- GcA=OnAf+miAm and matrix.Combining the static equilibrium condition with equation Effective Moduli of a Continuous Fiber-Reinforced Lamina 823) 9.22 621 620 819 318

Composite modulus energy terms can be simplified as and strains are uniform over the RVE and using equations(3.20),the strain Again making the mechanics of materials assumption that the stresses energy in the matrix,U: FIGURE 3.6 sented as the sum of the strain energy in the fibers,U,and the strain stress,the total strain energy stored in the composite,U can be repre- is possible by using a strain energy approach.Under the given state of Composites,206-217.) Further insight into the micromechanics of the longitudinal loading case for B-glass/polyester.(From Adams,R.D.,1987.Engineered Materials Handbook,Vol.1, elementary mechanics of materials models,(b)Comparison of predicted and measured E Variation of composite moduli with fiber volume fraction(a)Predicted E and E2 from 包 Fiber volume fraction Y28a6 E.3.23 E,GPa Fiber volume fraction,vr 010203040.506 Rule of mixtures A3:504m A d=20 jm .d=30 um Principles of Composite Material Mechanics 0.5 8350 G355) 25a 3.2 E 105ps Thus,the assumption of equal strains,which led to equation (3.23).is valid we find that a=2.0884,b1=0.1093,a1/b1=Gn/Gm =19.1,and Ea/Em =1.00 equation(3.24)leads to Em =0.55x10 psi (3.79 GPa) En =Er2 =10.5x10 psi (72.4 GPa) E8-1.53X100P81G0.55GPa1:-04B E-5.05X100p614.82Gpa2n-D.55 measured properties of an E-glass/epoxy composite [9], fiber strain to the matrix strain can then be found.For example,using the when composite,fiber,and matrix properties are known.The ratio of the tion(3.27)and equation (3.28)can be solved simultaneously for a and b to derive these equations.To check the strain distribution,however,equa- Note that we did not assume equal strains in fibers and matrix in order Substitution of equation(3.26),equation (3.20),and equation (3.25)in avr+biVm =1 of mixtures for stress,equation (3.19),leads to where a and bi are constants.Substitution of equation(3.26)in the rule the matrix be defined in terms of the composite stress as follows: strains is not made?"In order to proceed,let the stresses in the fibers and approach also allows us to ask,"What happens if the assumption of equal the rule of mixtures given by equation (3.23).But the strain energy with the assumption of equal strains from equation(3.22),again leads to is easily shown that substitution of equation(3.25)in equation(3.24),along ratios of the fiber and the matrix,so the approximation is justified [8].It to be of the order of the square of the difference between the Poisson's tions leading to equations [3.201).This neglected term has been shown strains at the fiber/matrix interface has been neglected(recall the assump- In this approximation,the strain energy due to the mismatch in Poisson Effective Moduli of a Continuous Fiber-Reinforced Lamina 929 328 C26

the composite. EXAMPLE 3.3 interphase. FIGURE 3.7 for the interphase material and extending the assumption of equal strains Now supplementing equation(3.20)with a similar stress-strain relationship noted by the subscript i here,with the addition of a third term representing the interphase,as de- rule of mixtures for longitudinal composite stress in equation(3.19)applies equal the sum of the forces acting on the three materials.Accordingly,the equilibrium requires that the total resultant force on the composite must Solution.The three constituent materials are arranged in parallel;so static together,derive the micromechanics equation for the longitudinal modulus,Eof Assuming that the three materials are linear elastic,isotropic,and securely bonded packing array geometry,it has been referred to as a "self-consistent model"[8] the geometrical features of this model are not associated with any specific fiber- the matrix materials and either the fiber material or a fiber-sizing material.Since phase regions may be created during processing as a result of interactions between the fiber,which has different properties from either the fiber or the matrix.Inter- the fiber/matrix interphase.The fiber/matrix interphase is a region surrounding approximated by three concentric cylinders representing the fiber,the matrix,and As shown in figure 3.7,an RVE for a three-phase unidirectional composite is assumption leading to the equation for the transverse modulus. approach will be used again in the next section to check the validity of an for this material,as it apparently is for other composites.The strain energy Self-consistent RVE for three-phase composite,including fiber,matrix,and fiber/matrix Fiber,Ee Interphase,E Matrix,Em Ga=GrVr+GmUm+Givi Principles,of Composite Material Mechanics 83-8217+2m2um (3.32)can be rearranged to get the rule of mixtures for transverse strains: the length fractions must be equal to the volume fractions,and equation Since the dimensions of the RVE do not change along the 1 direction, and equation(3.30)now becomes 83-01839+2mam It follows from the definition of normal strain that transverse displacements in the fiber,6r2,and the matrix,8m2: composite displacement,82,must equal the sum of the corresponding modulus,E2.Geometric compatibility requires that the total transverse shown in figure 3.5(c),the response is governed by the effective transverse If the RVE in figure 3.5(a)is subjected to a transverse normal stress,2,as 3.2.2 Transverse Modulus respectively and j=1,2,....n. where E and v;are the modulus and volume fraction of the jth constituent, mixtures for the longitudinal composite modulus is together and arranged in parallel as in figure 3.7,the generalized rule of where the diameters DDand D are defined in figure 3.7.Indeed,for a composite having any number of constituents,n,that are securely bonded in the constituents(eq.[3.221)to the interphase material as well,we get another rule of mixtures: Effective Moduli of a Continuous Fiber-Reinforced Lamina 3.33 8·32 830

strain: We now express the fiber and matrix strains in terms of the composite additional insight into the micromechanics of the transverse loading case. As with the longitudinal case,the strain energy approach provides section 3.5,the experimental data falls well above the curve. volume fractions.This turns out to be the correct trend,but,as shown in significant improvement in the transverse modulus only at high fiber values of fiber volume fraction,(i.e.,vr=0 and vr=1.0),but it predicts equation(3.36)gives the same result as equation (3.23)at the extreme (3.36)is generally not acceptable for design use.As shown in figure 3.5(a), approach to show that the resulting stresses are not equal.Thus,equation fiber and matrix are not necessarily equal,and we will use a strain energy the fiber-packing arrangement is such that the forces and areas for the equal areas normal to the 2 direction.In the actual composite,however, equal for the series arrangement,and both fiber and matrix blocks have stresses is valid because equilibrium requires that the forces must be From the RVE in figure 3.5,it would seem that the assumption of equal transverse modulus: equal,equation (3.35)reduces to the "inverse rule of mixtures"for the If we assume that the stresses in the composite,matrix,and fiber are all E2 solution.Combining equation(3.34)and equation (3.33),we get mechanics of materials solution and a more rigorous theory of elasticity interface [10,11].This is another example of the difference between a complex state of stress due to the mismatch in Poisson strains at the tudinal case,the inclusion of such strains would lead to a much more where the Poisson strains have again been neglected.As with the longi- The 1-D Hooke's laws for this case are u09 Principles of Composite Material Mechanics .3 2.36 3.35 of matrix. formulation: where va2 is the major Poisson's ratio of fiber and vm the Poisson's ratio V12 Vi12Uf+VmUm with both the 1 and the 2 directions.The result is another rule of mixtures be found by solying the geometric compatibility relationships associated when the only nonzero stress is a normal stress along the 1 direction,can the orthotropic lamina.The major Poisson's ratio,which is defined as most often used as the two remaining independent elastic constants for The major Poisson's ratio,vi2,and the in-plane shear modulus,Gi2,are 3.2.3 Shear Modulus and Poisson's Ratio ulus will be discussed later. well.More accurate alternative design equations for the transverse mod- for this material and is apparently not valid for most other composites as stresses in fibers and matrix,which led to equation(3.36),is not justified sponding stress ratio is 6r2/om2=5.63.Thus,the assumption of equal a2=0.432,b2=1.465,the strain ratio a/b2=Er2/Em2 =0.295,and the corre- solving equation(3.38)and equation(3.39)simultaneously,we find that Using the properties for the E-glass/epoxy given in equation(3.29)and equal stresses in the fibers and the matrix in order to get equation(3.39) has again been neglected.It is important to note that we did not assume where the strain energy due to the Poisson strain mismatch at the interface energy expression,equation(3.24),we find that gous to equation (3.25)for the transverse loading case and the strain By substituting equation(3.37)and equation(3.34)in equations analo- 21+70m-1 patibility expression,equation(3.33)yields where a2 and b2 are constants.Substitution of equation(3.37)in the com- Effective Moduli of a Continuous Fiber-Reinforced Lamina 3.元1) 239

EXAMPLE 3.4 The transverse modulus is roughly estimated by equation(3.36): modulus of matrix. inverse rule of mixtures: 0482 H0.82X10mP61(6.65GP E:-82X10000.506-+05X10000.482-16.43x100P81118GPg Solution.The longitudinal modulus is given by equation(3.23) maximum possible values of Er and E2? moduli of the composite.Given these fiber and matrix materials,what are the GPa),and Em=0.5x 106 psi(3.45 GPa).Estimate the longitudinal and transverse 3.2 have the properties En=32.0 x 106 psi(220 GPa),Ep=2.0 x 106 psi(13.79 The constituent materials in the composite described in example 3.1 and example tions will be discussed in the following sections. better equations for estimating the in-plane shear modulus.Such equa- are in fact not equal.As with the transverse modulus,we need to find that used in section 3.2.2 can be used here to show that the shear stresses stresses are not equal as assumed.A strain energy approach similar to As we might expect,this equation is not very accurate because the shear where Ga2 is the shear modulus of fiber in the 12 plane and Gm=shear assumption of equal shear stresses in fibers and matrix,leads to another is,geometric compatibility of the shear deformations,along with the approach similar to that which was used for the transverse modulus.That An equation for the in-plane shear modulus can be derived using an Y2=2E the average engineering shear strain in the 12 plane. where oc2 is the average composite shear stress.in the 12 plane and The effective in-plane shear modulus is defined as(fig.3.5[d]) metric compatibility relationships leading to the solution are valid. design purposes.As in the case for the longitudinal modulus,the geo- Equation(3.41)is generally accepted as being sufficiently accurate for Principles of Composite Material Mechanics 943 3.3) EXAMPLE 3.5 based on invalid assumptions.and agreement with experimental resuilts is models for E2 and Gi2 are of questionable value,however,because they are models for E and vi2 are good enough for design use.The corresponding As shown in the previous section,the elementary mechanics of materials Improved Mechanics of Materials Models to the ratio of fiber volume fraction to the matrix volume fraction. to matrix stress is ratio would increase dramatically to 624,however,since it is proportional same since it is independent of the fiber volume fraction.The strain energy possible fiber volume fraction of 0.907,the stress ratio would remain the that is almost the same as the stress ratio.If the composite had the maximum EmEm! 3200500-00 0.5(0.482) and equation(3.22),the ratio of fiber strain energy to matrix strain energy is higher than the matrix modulus.From equation 3.25(b),equation 3.25(c) Thus,the fiber carries most of the stress since the fiber modulus is always 820-640 Solution.From equation(3.20)and equation(3.22),the ratio of fiber stress with that stored in the matrix. in the fiber and matrix materials.Compare the strain energy stored in the fibers For longitudinal loading of the composites in example 3.4,compare the stresses stiffness-to-weight ratios than conventional metallic structural materials. about 20%of the density of steel.Composites typically have much greater the same as the modulus of steel,but the density of the composite is only the longitudinal modulus of the graphite/epoxy composite is now about reinforcement is usually necessary in practical applications.Note also that content,the transverse modulus is still very low.Thus,some transverse E2=1.56 x 106 psi (10.75 GPa).Note that even with this maximum fiber properties are still highly anisotropic,with E1=29x 106 psi(200 GPa)and a close-packed triangular array (eq.[3.13]),the corresponding composite composite has the theoretical maximum fiber volume fraction of 0.907 for As expected,the composite is highly anisotropic,with E1>>E2.If the Effective Moduli of a Continuous Fiber-Reinforced Lamina 三