
structures. figure 7.1 are for laminates consisting of plies of the same material.For by enclosing the set of angles in parentheses.The examples shown in overbar.Sets of ply angles that are repeated in the laminate are identified having an odd number of plies,the center ply angle is denoted by an subscript on the appropriate ply angle.In the case of symmetric laminates plies having the same orientations can be described by using a numerical be described by listing only the ply angles for the top half of the laminate and by using the subscript "s"outside the brackets,and that adjacent shown by the examples in figure 7.1.Note that symmetric laminates can top surface to the bottom surface and enclosed in square brackets,as code is that ply angles,separated by slashes,are listed in order from the orientation code has evolved in the composites literature.The basis of the nations of ply orientations and stacking sequences in laminates,a laminate Because of the need for adequate description of many possible combi- laminate strength are also discussed. prediction of thermal and residual stresses, interlaminar stresses,and that may occur in laminates.Other aspects of laminate analysis,such as (CLT),which makes it possible to analyze the complex coupling effects followed by a discussion of the more general Classical Lamination Theory ering a simplified theory of laminated beams in pure flexure.This will be In this chapter,the analysis of laminates will be introduced by consid- struction considerably enhance the design flexibility inherent in composite ply orientations,and ply-stacking sequences offered by laminated con- in a structural unit.The virtually limitless combinations of ply materials, laminae or plies oriented in the desired directions and bonded together are more likely to be in the form of laminates consisting of multiple element because of its poor transverse properties.Composite structures unidirectional lamina alone is generally not very useful as a structural development of theories for the analysis of composite structures,the While an understanding of lamina mechanical behavior is essential to the 7.1 Introduction Analysis of Laminates

FIGURE 7.1 芦 ory is quite restricted,it yields considerable insight into the analysis of elementary mechanics of materials.Although the application of this the- in pure flexure can be developed from the Bernoulli-Euler theory of nated beam that is subjected to pure bending.A theory of laminated beams For the purpose of analysis,the simplest laminated structure is a lami- Theory of Laminated Beams in Pure Flexure on the ply angles may be used to identify the ply material. hybrid laminates having plies of different materials,additional subscripts Examples of laminate stacking sequences and the corresponding laminate orientation codes +45 115 45 160午44/009o 5。 e 。 446/02090s 10010035l 1(01700945l .300 1001305 Principles of Composite Material Mechanics FIGURE 7.2 z from the neutral surface is given by the familiar equation As a result of assumption 1,the longitudinal normal strain at a distance The only stress components present are o,and t ply interfaces 4.The plies are perfectly bonded together,so that no slip occurs at tations are either 0 or 90). 3.Each ply is linearly elastic with no shear coupling(ie.,ply orien- arranged about the xy plane). about the neutral surface (i.e.,the plies are symmetrically 2.The beam has both geometric and material property symmetry the beam remain plane and normal during flexure. 1.Plane sections that are initially normal to the longitudinal axis of M.The assumptions used in developing the analysis are as follows: shown in figure 7.2 before and after the application of a bending moment A section of a rectangular laminated beam of depth h and width b is here is based on the analysis of Pagano [1]. general CLT,which is described in the next section.The theory described laminated structures and provides a natural introduction to the more An element of a laminated beam before and after the application of a bending moment Before deformation Analysis of Laminates After flexural deformation E

¥ relation is given by Recall that for a homogeneous,isotropic beam,the moment-curvature original ply,so that the total number of plies is now even. divide each ply into two identical plies having half the thickness of the Equation(7.6)can also be used for an odd number of plies if we simply (7.3)in equation (7.4)gives defined by the xy plane. 巴 20 thickness z;=jh/N and equation (7.5)becomes surface to the outside of the jth ply.For an even number of plies of uniform where N is the total number of plies and z is the distance from the neutral where the symmetry assumption 2 has been used.Substitution of equation be related to the longitudinal stresses by Static equilibrium requires that the applied bending moment M must equation(7.1)and equation(7.2),the longitudinal stress is seen to be (e,);is the longitudinal strain in the jth ply along the x direction.From where(E.);is the Young's modulus of ith ply along the x direction and From assumption 3,the longitudinal stress in the jth ply is given by the angle defined in figure 7.2,and z the distance from neutral surface where p is the radius of curvature of the neutral surface during flexure, Principles of Composite Material Mechanics 园 金 8 8 (7.7)to get buckling load,Pfor a laminated beam can be estimated by the formula where p is the applied tip load and L is the beam length.The Euler 三 in figure 7.3 would be given by the familiar equation and the maximum deflection at the tip of the laminated cantilever beam would be of the form Young's modulus. ferential equation for the transverse deflection,w,of a laminated beam equations from elementary mechanics of materials.For example,the dif- flexural modulus in place of the Young's modulus in the beam deflection The deflections of laminated beams can now be calculated by using the ing sequence and the ply moduli.That is,if the properties do not change through the thickness of a beam,the flexural modulus is the same as the modulus of the homogeneous isotropic beam,depends on the ply-stack- Thus,the flexural modulus of the laminated beam,unlike the Young's 冬 or for an even number of plies we can combine equation(7.6)and equation flexural modulus of the laminated beam can be expressed as Combining equation(7.5)and equation(7.7),we find that the effective effective flexural modulus of the beam(which is same as Young's modulus of the beam material for a homogeneous,isotropic beam). whereIw=zdA=/12 is the moment of inertia of the cross section about the neutral axis (y axis),A the cross-sectional area,and Ef the Analysis of Laminates 是 G10 8 品 务
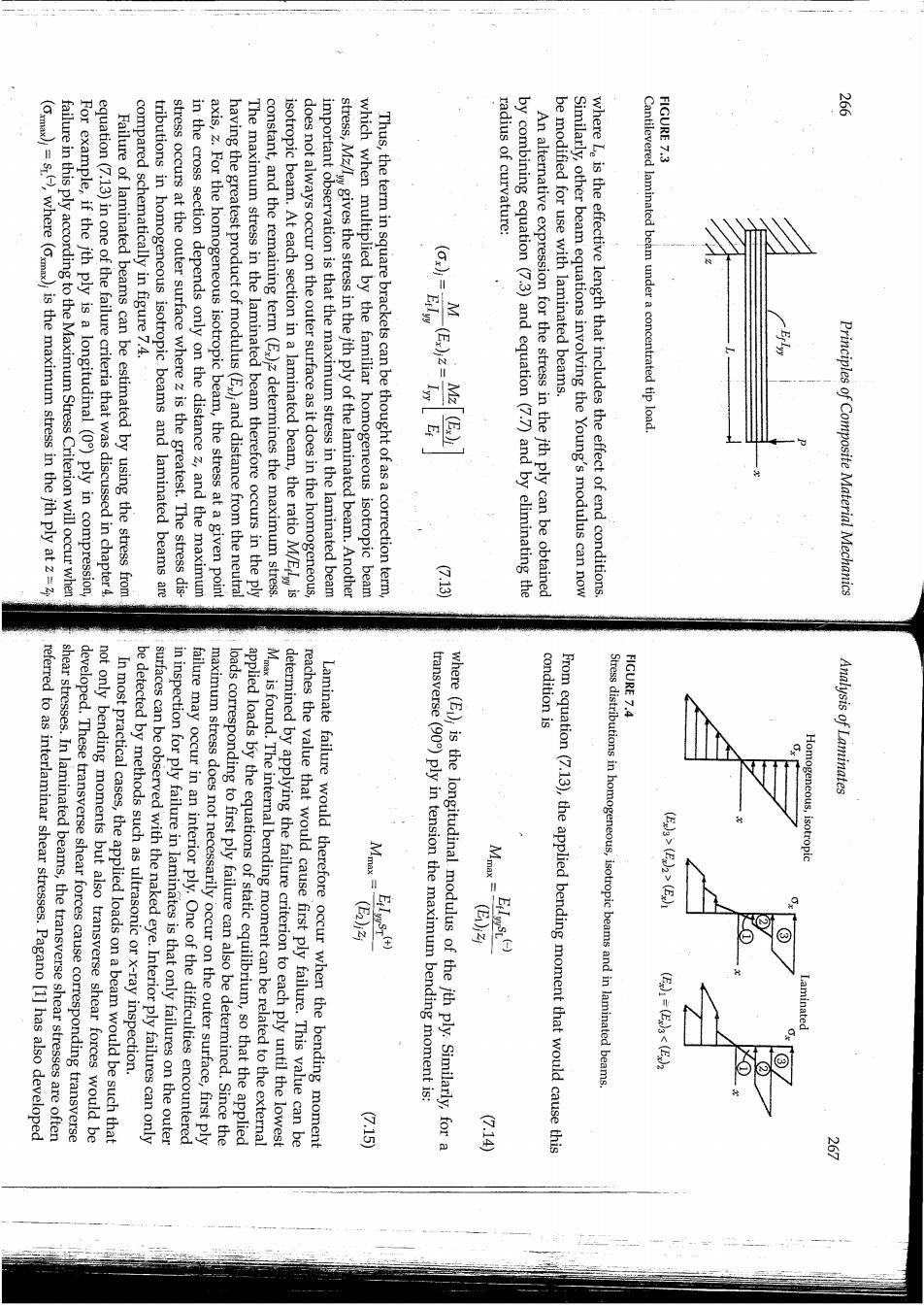
FIGURE 7.3 (Cmax)=s,where (max)is the maximum stress in the jth ply at z= failure in this ply according to the Maximum Stress Criterion will occur when For example,if the ith ply is a longitudinal (0)ply in compression, equation(7.13)in one of the failure criteria that was discussed in chapter 4. Failure of laminated beams can be estimated by using the stress from compared schematically in figure 7.4. tributions in homogeneous isotropic beams and laminated beams are stress occurs at the outer surface where z is the greatest.The stress dis- in the cross section depends only on the distance z,and the maximum axis,z.For the homogeneous isotropic beam,the stress at a given point having the greatest product of modulus(E,);and distance from the neutral The maximum stress in the laminated beam therefore occurs in the ply constant,and the remaining term (E)z determines the maximum stress. isotropic beam.At each section in a laminated beam,the ratio M/Eis does not always occur on the outer surface as it does in the homogeneous, important observation is that the maximum stress in the laminated beam stress,Mz/Iw gives the stress in the jth ply of the laminated beam.Another which when multiplied by the familiar homogeneous isotropic beam Thus,the term in square brackets can be thought of as a correction term, radius of curvature: by combining equation (7.3)and equation(7.7)and by eliminating the An alternative expression for the stress in the ith ply can be obtained be modified for use with laminated beams. Similarly,other beam equations involving the Young's modulus can now where Le is the effective length that includes the effect of end conditions. Cantilevered laminated beam under a concentrated tip load Principles of Composite Material Mechanics 会 condition is FIGURE 7.4 shear stresses.In laminated beams,the transverse shear stresses are often referred to as interlaminar shear stresses.Pagano [1]has also developed not only bending moments but also transverse shear forces would be developed.These transverse shear forces cause corresponding transverse be detected by methods such as ultrasonic or x-ray inspection. In most practical cases,the applied loads on a beam would be such that in inspection for ply failure in laminates is that only failures on the outer surfaces can be observed with the naked eye.Interior ply failures can only failure may occur in an interior ply.One of the difficulties encountered maximum stress does not necessarily occur on the outer surface,first ply applied loads by the equations of static equilibrium,so that the applied loads corresponding to first ply failure can also be determined.Since the Mis found.The internal bending moment can be related to the external reaches the value that would cause first ply failure.This value can be determined by applying the failure criterion to each ply until the lowest Laminate failure would therefore occur when the bending moment where(E);is the longitudinal modulus of the jth ply.Similarly,for a transverse (90)ply in tension the maximum bending moment is: From equation(7.13),the applied bending moment that would cause this Stress distributions in homogeneous,isotropic beams and in laminated beams. Analysis of Laminates 元ss 闐 公10

direction, FIGURE 7.5 多 static equilibrium of the element with respect to the forces along the x must act at the inner edge of the kth ply,as shown in figure 7.5.From under these normal stresses alone,the interlaminar shear stress, as shown in figure 7.5.Since the element cannot be in static equilibrium on the two faces of the jth ply in a differential element must be different, too,must the normal stress,o.This means that the normal stresses acting (7.13),we see that if the bending moment changes with respect to x,so, must change along the length of the beam(the x direction).From equation Thus,the presence of the shear force implies that the bending moment M,is related to the transverse shear force,V,by the equation Recall from the mechanics of materials [2]that the bending moment, stresses,as summarized here. 兵 a mechanics of materials approach for estimating these interlaminar shear for static equilibrium when the bending moment varies along the length. Differential element of a laminated beam showing interlaminar shear stress that is necessary ↓4 ↓@ +t号 Principles of Composite Material Mechanics 160 where which is where for a laminated beam Thus,the transverse shear stress is given by for a homogeneous isotropic beam equation for transverse shear stress in a homogeneous isotropic beam, Equation (7.20)is seen to be similar to the "mechanics of materials" for a rectangular beam having an even number of plies of uniform thick- ness,zj=jh/N,and equation (7.19)reduces to integrating,we find that the interlaminar stress at the inner edge of the Substituting equation (7.13)and equation(7.16)in equation(7.18)and Analysis of Laminates d(odz G23 G22 G211 (7.20) G13 多

EXAMPLE 7.1 FIGURE 7.6 we can use equation (7.9)for the flexural modulus in both cases.For the stacking sequences are different.Since the ply thicknesses are all the same, Solution.The total number of plies is N=6 in each case,and only the have the same thickness. 5x 106 psi (34.48 GPa).and E2=1.5 x 106 psi (10.34 GPa),and the plies all having stacking sequences of [0/90/0]and [90/0/901 The ply moduli are E= Determine the flexural and Young's moduli of E-glass/epoxy laminated beams stresses,will be discussed later. nated plates along with failure criteria,which include the interlaminar Both normal and shear components of the interlaminar stresses in lami- cussed in chapter 4 were based only on in-plane stresses in the lamina. composites known as delamination.Recall that the failure criteria dis- Interlaminar stresses are responsible for an important failure mode in stress distribution departs significantly from the parabolic distribution. (7.22).For a small number of plies,however,the laminated beam shear expected to approach the parabolic distribution described by equation increases,the shear stress distribution for the laminated beam can be B,is shown for both types of beams in figure 7.6.As the number of plies The shear stress distribution,as governed by the variation of the factor beams with a small number of plies and a large number of plies. homogeneous,isotropic beams and for laminated beams.Results are given for laminated Variation of shear stress,as governed by the factor B,across half the beam thickness for Many plies Laminated,large N Homogeneous isotropic : Few plies -Laminated,small N -Homogeneous isotropic Principles of Composite Material Mechanics and thickness is governed hy the EXAMPLE 7.2 distribution of normal and shear stresses through the thickness of the beam. Assume a ply thickness of 0.01 in (0.254 mm). For the [90/0/90],E-glass/epoxy beam described in example 7.1,sketch the result regardless of the ply-stacking sequence,as long as the number of longitudinal and transverse plies remains unchanged). depend on the stacking sequence (i.e.,the rule of mixtures gives the same not the same as the Young's modulus.The Young's modulus does not Note that the flexural modulus depends on the stacking sequence and is For the [90/0/901,beam E=1.5(+5(x10psi=2.66x10psi (18.34 GPa) fraction of transverse(90)plies.Therefore, (26.4GPa) where v1=volume fraction of longitudinal (0)plies and v2 volume The Young's modulus,or extensional modulus,can be estimated by using the rule of mixtures =4.09x10psi(28.2 GPa) xR-H+Oe一++—多交法 Analysis of Laminates

3 FIGURE 7.7 Stress distributions for the beam described in example 7.2. variation of S across the thickness. edge of ply number 2. k:(GX100(0.02)-10X104k: Kl.5X100/0.02-80x100k: K15X100)(008)-45X108k: variation of (E.)z. (a)Normal stresses 9 10.108X 品 (b)Shear stresses y distribution can then be determined to within a constant K2 by finding the as (T)k=K2S,where s is defined by equation (7.21).The shear stress 2bhEr can be set equal to a constant,K2 and the shear stress can be written and equation (7.21).For a given cross section,however,the ratio 3V/ with an even number of uniform thickness plies is given by equation(7.20) The interlaminar shear stress at the inner surface of the kth ply for a beam outer surface as in a homogeneous isotropic beam but,rather,at the outer figure 7.7(a).It is seen that the maximum normal stress occurs not on the The predicted distribution of o,across the thickness is plotted in For the inner surface of ply number 1 (on the neutral surface),,=0. :/k801X51-)100(0601X5。私1大:1 Fo For the inner surface of ply number 2,,=Ki(5x 106)(0.01)=5x 104K1. Similarly,for the outer surface of ply number 2,the stress is ox= For the inner surface of ply number 3,z=0.02 in and the stress is o,= modulus is (E )a=E2 =1.5 x 106 psi,z=0.03 in and the stress is o,= For the outer surface of ply number 3(the outer transverse ply),the ply be determined to within a constant Ki=M/Eby finding the corresponding Principles of Composite Material Mechanics Fork=3 For k=2 for k=1 distribution is substantial,however,because of the small number of plies. the shear stress at the outer surface is zero.The deviation from the parabolic ness is plotted in figure 7.7(b).As with the shear stress in a homogeneous isotropic beam,the maximum shear stress occurs on the neutral surface and surface must be stress-free The predicted distribution ofacross the thick- the outer surface.This also satisfies the boundary condition that the outer material in this"imaginary ply,"S=0 and the shear stress must be zero on of ply number 3 or the outer surface of the laminate.Since there is no Finally,for k=4,equation(7.20)gives the shear stress at the inner surface of an"imaginary ply"whose inner surface is the same as the outer surface Analysis of Laminates -0.833x100pa1(6.74GRa :2.5X1022647.24GPa 装家 2166x100ps118.a4Gpa) 615((+1.5x10 兰 From equation(7.20)and equation(7.21)

出 along arbitrary directions with respect to the xu axes. the principal material axes of the orthotropic laminae oriented 1.The plate consists of orthotropic laminae bonded together,with static analysis are [10]: are u,v,and w,respectively.The basic assumptions relevant to the present lies in the xy plane.The displacements at a point in thex,y,and z directions its origin on the middle surface of the plate,so that the middle surface laminated plate analysis.The xyz coordinate system is assumed to have Figure 7.8 defines the coordinate system to be used in developing the ing the equations of motion,only the static analysis will be considered here. Whitney [10].Although Whitney has presented a general analysis includ- mation hypothesis are now derived following the procedure outlined by plate.The laminate force-deformation equations resulting from this defor- from the classical homogeneous plate theory can be used for the laminated be continuous.These assumptions mean that the deformation hypothesis which means that displacements across lamina interfaces are assumed to allowed,and the interfacial bonds are not allowed to deform in shear, as a unitary,nonhomogeneous anisotropic plate.Interfacial slip is not that the individual laminae are perfectly bonded together so as to behave Although the laminate is made up of multiple laminae,it is assumed classical plate theory [9]. placement relationships(Appendix B)are the same as those used in the hypothesis,the equilibrium equations(Appendix A),and the strain-dis- strain relationships.Other elements of the theory such as the deformation of homogeneous,isotropic plates [9]is in the form of the lamina stress- Hoff [8].The major difference between this theory and the classical theory [41,Reissner and Stavsky [5],Stavsky [6],Lekhnitskii [7],and Stavsky and in the 1950s and 1960s by investigators such as Smith [31,Pister and Dong What is now referred to as the CLT has apparently evolved from work and that interlaminar stresses are neglected. tion of the CLT is that each ply is assumed to be in a state of plane stress bending and twisting moments are included.The most important limita- tions.In addition,in-plane loading due to shear and axial forces and both complex combinations of extensional,flexural,and torsional deforma- trarily oriented plies may have various coupling effects that may lead to Using this theory,we can analyze nonsymmetric laminates whose arbi- discuss the more general CLT,which does not have these restrictions. that are subjected to a single bending moment.In this section,we will and instructive,it is restricted to symmetric laminates without coupling While the simplified theory of laminated beams in pure flexure is useful Theory of Laminated Plates with Coupling Principles of Composite Material Mechanics the r and v dirertions placements can be expressed as thickness. FIGURE 7.8 where uand are the tangential displacements of the middle surface along normal during deformation.According to assumptions 6 and 7,the dis- coordinate. tion hypothesis that normals to the middle surface remain straight and ply,whereas assumptions 5 and 6 together define the Kirchhoff deforma- Assumption 5 is a result of the assumed state of plane stress in each 10.Transverse shear stresses Tand ty vanish on the plate surfaces defined by z=t/2. 9.The plate thickness t is constant. 8.Each ply obeys Hooke's law. The transverse normal strain e,is negligible. Tangential displacements u and v are linear functions of the 5.Transverse shear strains Y and Y are negligible. 4.The in-plane strains ey and Ysy are small compared with unity. The displacements u,v,and w are small compared with the plate along the plate edges,a and b. 2.The thickness of the plate,t,is much smaller than the lengths Coordinate system and stress resultants for laminated plate Analysis of Laminates (7.24)

and that 之 ment relations for the in-plane strains(Appendix B),we find that Substituting equations(7.24)and equations(7.27)in the strain-displace- functions of the z coordinate as follows: 是 笔 P0.0 20010 verse shear strains and using assumption 5,we find that (7.24)in the strain-displacement equations(Appendix B)for the trans- only develop the CLT based on equation (7.24).Substituting equations Such a theory is beyond the scope of this book,however,and we will which is based on the assumption that the displacements are nonlinear lamination theory.For example,Christensen [11]describes one such theory, transverse shear deformations,it is necessary to use a so-called higher-order for possible warping of the cross section of the laminate and resulting =w(x,y).At this point it is appropriate to mention that in order to account displacement of any point having the samex and y coordinates,so w(x,y) displacement at the middle surface,w(x,y),is the same as the transverse Principles of Composite Material Mechanics G28 国 G25 equations.Similarly,in the laminated plate analvsis the midlane related to the loads on the structure by additional static equilibrium stress,equation (7.13),was developed.The bending moment.can be ship in equation (7.4).The result was that a more useful equation for to the applied bending moment by using the static equilibrium relation- known and is difficult to measure.Thus,the lamina stress was related to be of limited practical use because the curvature is not generally In the laminated beam analysis,equation(7.3)for lamina stress is seen sion and shear.In addition,the laminated plate analysis includes the stresses due to shear coupling,as discussed in chapter 2. the laminated plate analysis gives the 2-D lamina stresses y and due to bending and twisting curvatures and to the midplane biaxial exten- only gives the uniaxial stress,ox,due to the bending curvature,whereas equation(7.3),we notice several differences.The laminated beam analysis plate stresses in equations(7.31)with the laminated beam stress given by where the subscript k refers to the kth lamina.Comparing the laminated before deformation. Analysis of Laminates 9 g relationships from equations (2.35)as follows: 9 第十 樂十茶 may be found by substituting equations(7.28)into the lamina stress-strain surface,the stresses along arbitrary xy axes in the kth lamina of a laminate Since equations(7.28)give the strains at any distance z from the middle with out-of-plane twisting of the middle surface,which lies in the xy plane the middle surface in the yz plane.K is a twisting curvature associated in the xz plane and K,is a bending curvature associated with bending of K,is a bending curvature associated with bending of the middle surface 1 and the curvatures of the middle surface are where the strains on the middle surface are 者 G50 G.29

FIGURE 7.9 月 here is different from that used in figure 7.2 for the laminated beam analysis. Laminated plate geometry and ply numbering system.Caution:The ply numbering system Middle surface in equation (7.32)and equation(7.33),respectively,we find that Substituting the lamina stress-strain relationships from equations(7.31) kth lamina,as shown in figure 7.9. zk the corresponding distance from middle surface to outer surface of the the distance from middle surface to inner surface of the kth lamina,and where t is the laminate thickness,()the stress in the kth lamina,- and the moment per unit length,My is given by For example,the force per unit length,Na,is given by are also referred to as stress resultants. moments.The forces and moments per unit length shown in figure 7.8 nient to use forces and moments per unit length rather than forces and tions more useful.In the laminated plate analysis,however,it is conve- moments by static equilibrium equations in order to make these equa- and curvatures in equations(7.31)must be related to applied forces and Principles of Composite Material Mechanics 圣 是 是 in matrix form as 三 we find that and Analysis of Laminates 2 的 吧 4 0 君 and the laminate-bending stiffnesses are given by The laminate-coupling stiffnesses are given by 60 41/2402122 where the laminate extensional stiffnesses are given by 四 written in similar form,and the complete setof equations can be expressed where the subscripts i,j=1,2,or 6.The other stress resultants can be M:=Be+Bie+Bcy+Dukx+Dky+Diokxy Combining terms and rearranging equation(7.34)and equation(7.35) 4! G·c8 (7.37) G26 G35 三