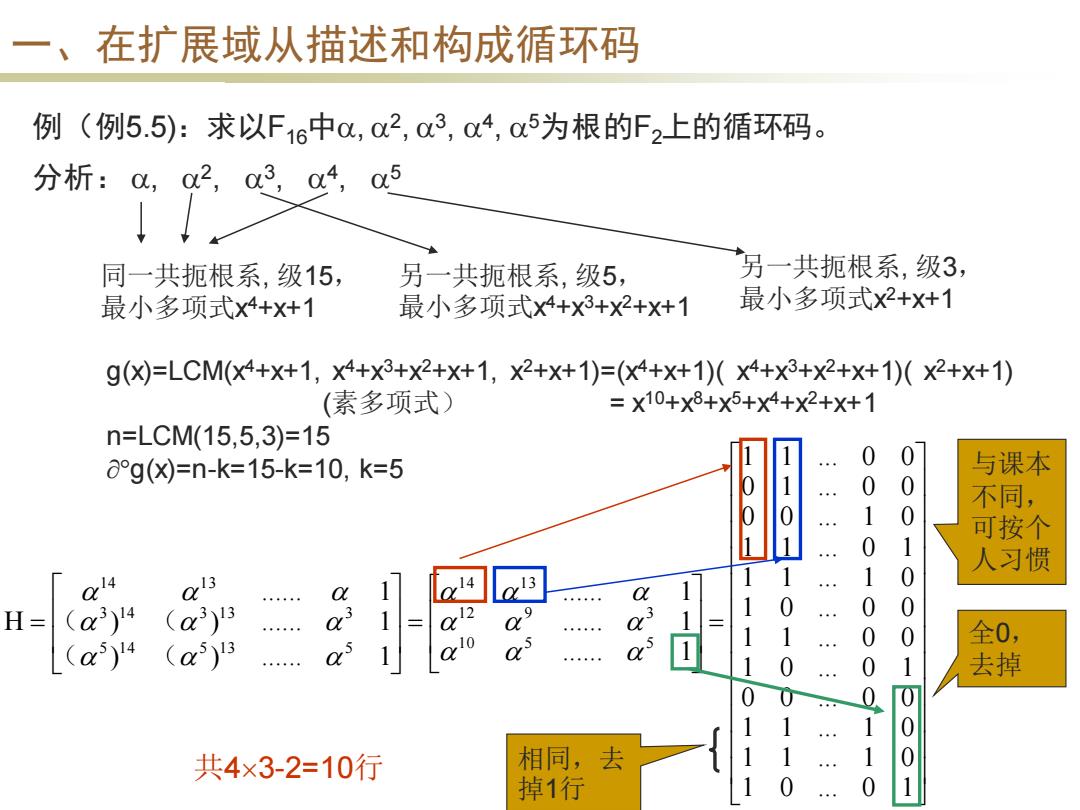
一 、在扩展域从描述和构成循环码 例（例5.5)：求以F16中o,02,03,04,05为根的F2上的循环码。 分析：，2,34,5 同一共扼根系，级15， 另一共扼根系，级5， 另一共扼根系，级3， 最小多项式x4+x+1 最小多项式x4+x3+x2+x+1 最小多项式x2++1 g()=LCM(x4+X+1,X4+x3+x2+x+1,X2+X+1)=(X4+x+1)(x4+x3+x2+X+1)(X2+x+1) (素多项式) =X10+Xx8+x5+x4+x2+X+1 n=LCM(15,5,3)=15 ag(X)=n-k=15-k=10,k=5 0 0 与课本 0 0 不同， 1 0 可按个 0 人习惯 1 0 1 1 H= (a3)4 (a3)13 0 0 0 1 0 全0， (a5)14 (a5)3 as 1 0 a 1 1 0 0 1 去掉 0 0 1 1 8 共4×3-2=10行 相同，去 0 掉1行 1 0 1一、在扩展域从描述和构成循环码 例（例5.5)：求以F16中, 2 , 3 , 4 , 5为根的F2上的循环码。 分析： , 2 , 3 , 4 , 5 同一共扼根系, 级15， 最小多项式x 4+x+1 另一共扼根系, 级5， 最小多项式x 4+x3+x2+x+1 另一共扼根系, 级3， 最小多项式x 2+x+1 g(x)=LCM(x4+x+1, x4+x3+x2+x+1, x2+x+1)=(x4+x+1)( x4+x3+x2+x+1)( x2+x+1) (素多项式） = x10+x8+x5+x4+x2+x+1 n=LCM(15,5,3)=15 g(x)=n-k=15-k=10, k=5                             =         =         = 1 0 ... 0 1 1 1 ... 1 0 1 1 ... 1 0 0 0 ... 0 0 1 0 ... 0 1 1 1 ... 0 0 1 0 ... 0 0 1 1 ... 1 0 1 1 ... 0 1 0 0 ... 1 0 0 1 ... 0 0 1 1 ... 0 0 ...... 1 ...... 1 ...... 1 ) ) ...... 1 ) ) ...... 1 ...... 1 H 1 0 5 5 1 2 9 3 1 4 1 3 5 1 4 5 1 3 5 3 1 4 3 1 3 3 1 4 1 3                   （ （ （ （ 与课本 不同， 可按个 人习惯 全0， 去掉 相同，去 掉1行 共43-2=10行