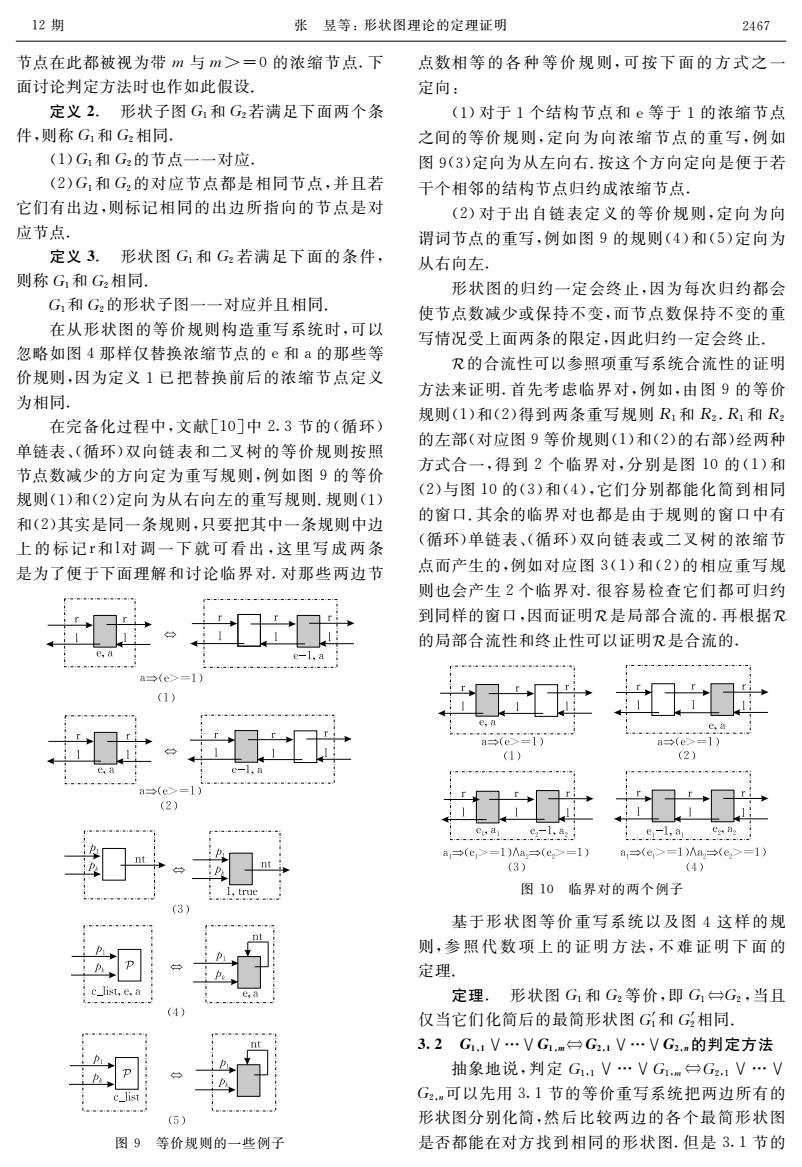
12期 张昱等：形状图理论的定理证明 2467 节点在此都被视为带m与m>=0的浓缩节点.下 点数相等的各种等价规则，可按下面的方式之一 面讨论判定方法时也作如此假设， 定向： 定义2.形状子图G1和G2若满足下面两个条 (1)对于1个结构节点和e等于1的浓缩节点 件，则称G1和G2相同. 之间的等价规则，定向为向浓缩节点的重写，例如 (1)G1和G2的节点一一对应。 图9(3)定向为从左向右.按这个方向定向是便于若 (2)G1和G2的对应节点都是相同节点，并且若 干个相邻的结构节点归约成浓缩节点· 它们有出边，则标记相同的出边所指向的节点是对 (2)对于出自链表定义的等价规则，定向为向 应节点。 谓词节点的重写，例如图9的规则(4)和(5)定向为 定义3.形状图G1和G2若满足下面的条件， 从右向左 则称G1和G2相同， 形状图的归约一定会终止，因为每次归约都会 G1和G2的形状子图一一对应并且相同. 使节点数减少或保持不变，而节点数保持不变的重 在从形状图的等价规则构造重写系统时，可以 写情况受上面两条的限定，因此归约一定会终止， 忽略如图4那样仅替换浓缩节点的e和a的那些等 R的合流性可以参照项重写系统合流性的证明 价规则，因为定义1已把替换前后的浓缩节点定义 方法来证明，首先考虑临界对，例如，由图9的等价 为相同 规则(1)和(2)得到两条重写规则R1和R2,R1和R2 在完备化过程中，文献[10]中2.3节的（循环） 的左部（对应图9等价规则(1）和(2)的右部)经两种 单链表、（循环）双向链表和二叉树的等价规则按照 节点数减少的方向定为重写规则，例如图9的等价 方式合一，得到2个临界对，分别是图10的(1)和 规则(1)和(2)定向为从右向左的重写规则.规则(1) (2)与图10的(3)和(4)，它们分别都能化简到相同 和(2)其实是同一条规则，只要把其中一条规则中边 的窗口.其余的临界对也都是由于规则的窗口中有 上的标记r和1对调一下就可看出，这里写成两条 (循环)单链表、（循环）双向链表或二叉树的浓缩节 是为了便于下面理解和讨论临界对.对那些两边节 点而产生的，例如对应图3(1)和(2)的相应重写规 则也会产生2个临界对.很容易检查它们都可归约 到同样的窗口，因而证明R是局部合流的.再根据R 的局部合流性和终止性可以证明R是合流的 (e 1》 (1) (2) (2 eu,a e-1,a es ag a→(e>=1)/Aa,=(e>=1) a,→fe>=1)/Aa,→(e>=1) (3) (4) 图10临界对的两个例子 基于形状图等价重写系统以及图4这样的规 则，参照代数项上的证明方法，不难证明下面的 定理 cJlist,e.a 定理.形状图G1和G2等价，即G1台G2,当且 仅当它们化简后的最简形状图G和G相同。 3.2G.1V…VG1.m台G21V…VG2.m的判定方法 抽象地说，判定G11V…VGm台G2.1V…V G2.m可以先用3.1节的等价重写系统把两边所有的 (5) 形状图分别化简，然后比较两边的各个最简形状图 图9等价规则的一些例子 是否都能在对方找到相同的形状图.但是3.1节的节点在此都被视为带犿与犿＞＝０的浓缩节点．下 面讨论判定方法时也作如此假设． 定义２．形状子图犌１和犌２若满足下面两个条 件，则称犌１和犌２相同． （１）犌１和犌２的节点一一对应． （２）犌１和犌２的对应节点都是相同节点，并且若 它们有出边，则标记相同的出边所指向的节点是对 应节点．定义３．形状图犌１和犌２若满足下面的条件， 则称犌１和犌２相同． 犌１和犌２的形状子图一一对应并且相同． 在从形状图的等价规则构造重写系统时，可以 忽略如图４那样仅替换浓缩节点的ｅ和ａ的那些等 价规则，因为定义１已把替换前后的浓缩节点定义 为相同．在完备化过程中，文献［１０］中２．３节的（循环） 单链表、（循环）双向链表和二叉树的等价规则按照 节点数减少的方向定为重写规则，例如图９的等价 规则（１）和（２）定向为从右向左的重写规则．规则（１） 和（２）其实是同一条规则，只要把其中一条规则中边 上的标记ｒ和ｌ对调一下就可看出，这里写成两条 图９等价规则的一些例子 是为了便于下面理解和讨论临界对．对那些两边节 点数相等的各种等价规则，可按下面的方式之一 定向： （１）对于１个结构节点和ｅ等于１的浓缩节点 之间的等价规则，定向为向浓缩节点的重写，例如 图９（３）定向为从左向右．按这个方向定向是便于若 干个相邻的结构节点归约成浓缩节点． （２）对于出自链表定义的等价规则，定向为向 谓词节点的重写，例如图９的规则（４）和（５）定向为 从右向左．形状图的归约一定会终止，因为每次归约都会 使节点数减少或保持不变，而节点数保持不变的重 写情况受上面两条的限定，因此归约一定会终止． $的合流性可以参照项重写系统合流性的证明 方法来证明．首先考虑临界对，例如，由图９的等价 规则（１）和（２）得到两条重写规则犚１和犚２．犚１和犚２ 的左部（对应图９等价规则（１）和（２）的右部）经两种 方式合一，得到２个临界对，分别是图１０的（１）和 （２）与图１０的（３）和（４），它们分别都能化简到相同 的窗口．其余的临界对也都是由于规则的窗口中有 （循环）单链表、（循环）双向链表或二叉树的浓缩节 点而产生的，例如对应图３（１）和（２）的相应重写规 则也会产生２个临界对．很容易检查它们都可归约 到同样的窗口，因而证明$是局部合流的．再根据$ 的局部合流性和终止性可以证明$是合流的． 图１０临界对的两个例子 基于形状图等价重写系统以及图４这样的规 则，参照代数项上的证明方法，不难证明下面的 定理．定理．形状图犌１和犌２等价，即犌１犌２，当且 仅当它们化简后的最简形状图犌′１和犌′２相同． ３２犌１，１∨…∨犌１，犿犌２，１∨…∨犌２，狀的判定方法 抽象地说，判定犌１，１∨…∨犌１，犿犌２，１∨…∨ 犌２，狀可以先用３．１节的等价重写系统把两边所有的 形状图分别化简，然后比较两边的各个最简形状图 是否都能在对方找到相同的形状图．但是３．１节的 １２期 张昱等：形状图理论的定理证明 ２４６７