
第39卷第12期 计 算机 学报 Vol.39 No.12 2016年12月 CHINESE JOURNAL OF COMPUTERS Dec,2016 形状图理论的定理证明 张昱陈意云李兆鹏 (中国科学技术大学计算机科学与技术学院合肥230026) (中国科学技术大学苏州研究院软件安全实验室江苏苏州215123) 摘要验证操作易变数据结构的指针程序仍面临很多挑战.数据结构中严重的指针别名显著地复杂化对操作这 些结构的程序的推理.为分析和验证操作易变数据结构的指针程序,文中提出了形状图逻辑.形状图是描述程序中 静态声明的堆指针变量和动态分配的结构体中指针域变量的指向的一种有向图,能准确表达指针的有效性和指针 之间的相等性,可用于判断两个访问表达式是否是别名.形状图逻辑是Hoa©逻辑的一种扩展,是一种直接将形状 图作为程序中指针断言集的程序逻辑.该文研究形状图的等价理论和蕴含理论以及它们的判定方法和应用.首先, 把形状图及其等价规则和蕴含规则分别类比为代数项及其等式规则和重写规则,像研究代数规范的理论那样来研 究形状图理论.该文定义了形状图的语法理论和语义理论,定义了形状图重写系统及其终止性、局部合流性和合流 性,然后得到基于形状图重写的形状图等价判定和蕴含判定的方法.其次,提出循环不变形状图和递归函数前后形 状图的自动推断方法,借助形状图理论的判定方法,该文把一个基于抽象解释的推断循环不变式的一般方法改编 成推断循环不变形状图的方法,由于计算终止的递归函数总有非递归的出口,可以先通过非递归路径得到函数的 后形状图的初值,然后再在递归路径上迭代求解.从而,可以像推断循环不变形状图那样来推断递归函数的前后形 状图.第三,参照Nelson-Oppen框架,提出形状图理论和整数理论组合的一种判定方法.对易变数据结构,除了关 心数据结构各节点是否连成预定的形状外,往往还关心数据在这些节点间的排列等特性,它们不能脱离易变数据 结构的形状特征而单独验证.为此,所提出的组合判定方法针对这类程序的验证条件的特点,利用程序分析阶段得 到的形状图对验证条件的前件中的符号断言按形状图的节点分组:然后运用整数理论为各节点推导出尽可能多的 性质:最后才交由定理证明器Z3去自动验证.这种方式有效地避免验证条件证明过程的不终止.基于形状图逻辑 以及文中的工作,我们所开发的程序验证系统原型减轻了自动定理证明器的负担,并且能验证易变数据结构上较 为复杂的程序,如有序循环双向链表、二叉排序树、伸展树、树堆、二叉平衡树和AA树的插入和删除函数 关键词形状图逻辑;形状分析:程序验证:自动定理证明:循环不变式的推断 中图法分类号TP311 D0I号10.11897/SP.J.1016.2016.02460 Theorem Proving for a Theory of Shape Graphs ZHANG Yu CHEN Yi-Yun LI Zhao-Peng (School of Computer Science and Technology,University of Science and Technology of China.Hefei 230026) (Softuure Security Laboratory.Suzhou Institute for Adwanced Study.University of Science and Technology of China.Suzhou.Jiangsu 215123) Abstract Programs manipulating mutable data structures present a challenge for verification. Deep aliasing inside data structures dramatically complicates reasoning statements manipulating these structures.To analyze and verify programs manipulating mutable data structures,we proposed the shape graph logic.Shape graphs describe point-to relations of statically declared heap pointer variables and pointer fields of heap objects.They precisely express the validity of pointers and the equalities between pointers,and can be used to judge whether two access expressions 收稿日期:2014-11-14:在线出版日期:2015-05-29.本课题得到国家“八六三”高技术研究发展计划项目基金(2012AA010901)、国家自然 科学基金(61170018,61229201)资助.张昱,女,1972生,博士,副教授,中国计算机学会(CCF)高级会员,主要研究方向为程序设计语 言的理论和实现技术、程序验证、确定性并行编程模型与运行时系统.E-mail:yuzhangt@ustc.edu.cn.陈意云,男,l946年生,教授,博士 生导师,中国计算机学会(CC℉)高级会员,主要研究领域为程序设计语言的理论和实现技术,程序验证、软件安全等.李兆鹏,男,1978年 生,博士,副研究员,中国计算机学会(CC℉)会员,主要研究方向为程序语言、程序验证、出具证明的编译器、自动定理证明
书 第39卷第12期 2016年12月 计 算 机 学 报 CHINESEJOURNALOFCOMPUTERS Vol.39No.12 Dec.2016 收稿日期:20141114;在线出版日期:20150529.本课题得到国家“八六三”高技术研究发展计划项目基金(2012AA010901)、国家自然 科学基金(61170018,61229201)资助.张昱,女,1972生,博士,副教授,中国计算机学会(CCF)高级会员,主要研究方向为程序设计语 言的理论和实现技术、程序验证、确定性并行编程模型与运行时系统.Email:yuzhang@ustc.edu.cn.陈意云,男,1946年生,教授,博士 生导师,中国计算机学会(CCF)高级会员,主要研究领域为程序设计语言的理论和实现技术、程序验证、软件安全等.李兆鹏,男,1978年 生,博士,副研究员,中国计算机学会(CCF)会员,主要研究方向为程序语言、程序验证、出具证明的编译器、自动定理证明. 形状图理论的定理证明 张昱陈意云李兆鹏 (中国科学技术大学计算机科学与技术学院合肥230026) (中国科学技术大学苏州研究院软件安全实验室江苏苏州215123) 摘要验证操作易变数据结构的指针程序仍面临很多挑战.数据结构中严重的指针别名显著地复杂化对操作这 些结构的程序的推理.为分析和验证操作易变数据结构的指针程序,文中提出了形状图逻辑.形状图是描述程序中 静态声明的堆指针变量和动态分配的结构体中指针域变量的指向的一种有向图,能准确表达指针的有效性和指针 之间的相等性,可用于判断两个访问表达式是否是别名.形状图逻辑是Hoare逻辑的一种扩展,是一种直接将形状 图作为程序中指针断言集的程序逻辑.该文研究形状图的等价理论和蕴含理论以及它们的判定方法和应用.首先, 把形状图及其等价规则和蕴含规则分别类比为代数项及其等式规则和重写规则,像研究代数规范的理论那样来研 究形状图理论.该文定义了形状图的语法理论和语义理论,定义了形状图重写系统及其终止性、局部合流性和合流 性,然后得到基于形状图重写的形状图等价判定和蕴含判定的方法.其次,提出循环不变形状图和递归函数前后形 状图的自动推断方法.借助形状图理论的判定方法,该文把一个基于抽象解释的推断循环不变式的一般方法改编 成推断循环不变形状图的方法.由于计算终止的递归函数总有非递归的出口,可以先通过非递归路径得到函数的 后形状图的初值,然后再在递归路径上迭代求解.从而,可以像推断循环不变形状图那样来推断递归函数的前后形 状图.第三,参照NelsonOppen框架,提出形状图理论和整数理论组合的一种判定方法.对易变数据结构,除了关 心数据结构各节点是否连成预定的形状外,往往还关心数据在这些节点间的排列等特性,它们不能脱离易变数据 结构的形状特征而单独验证.为此,所提出的组合判定方法针对这类程序的验证条件的特点,利用程序分析阶段得 到的形状图对验证条件的前件中的符号断言按形状图的节点分组;然后运用整数理论为各节点推导出尽可能多的 性质;最后才交由定理证明器Z3去自动验证.这种方式有效地避免验证条件证明过程的不终止.基于形状图逻辑 以及文中的工作,我们所开发的程序验证系统原型减轻了自动定理证明器的负担,并且能验证易变数据结构上较 为复杂的程序,如有序循环双向链表、二叉排序树、伸展树、树堆、二叉平衡树和AA树的插入和删除函数. 关键词形状图逻辑;形状分析;程序验证;自动定理证明;循环不变式的推断 中图法分类号TP311 犇犗犐号10.11897/SP.J.1016.2016.02460 犜犺犲狅狉犲犿犘狉狅狏犻狀犵犳狅狉犪犜犺犲狅狉狔狅犳犛犺犪狆犲犌狉犪狆犺狊 ZHANGYuCHENYiYunLIZhaoPeng (犛犮犺狅狅犾狅犳犆狅犿狆狌狋犲狉犛犮犻犲狀犮犲犪狀犱犜犲犮犺狀狅犾狅犵狔,犝狀犻狏犲狉狊犻狋狔狅犳犛犮犻犲狀犮犲犪狀犱犜犲犮犺狀狅犾狅犵狔狅犳犆犺犻狀犪,犎犲犳犲犻230026) (犛狅犳狋狑犪狉犲犛犲犮狌狉犻狋狔犔犪犫狅狉犪狋狅狉狔,犛狌狕犺狅狌犐狀狊狋犻狋狌狋犲犳狅狉犃犱狏犪狀犮犲犱犛狋狌犱狔,犝狀犻狏犲狉狊犻狋狔狅犳犛犮犻犲狀犮犲犪狀犱犜犲犮犺狀狅犾狅犵狔狅犳犆犺犻狀犪,犛狌狕犺狅狌,犑犻犪狀犵狊狌215123) 犃犫狊狋狉犪犮狋Programsmanipulatingmutabledatastructurespresentachallengeforverification. Deepaliasinginsidedatastructuresdramaticallycomplicatesreasoningstatementsmanipulating thesestructures.Toanalyzeandverifyprogramsmanipulatingmutabledatastructures,we proposedtheshapegraphlogic.Shapegraphsdescribepointtorelationsofstaticallydeclared heappointervariablesandpointerfieldsofheapobjects.Theypreciselyexpressthevalidityof pointersandtheequalitiesbetweenpointers,andcanbeusedtojudgewhethertwoaccessexpressions

12期 张昱等:形状图理论的定理证明 2461 are aliases or not.The shape graph logic is an extension to Hoare logic,which directly uses shape graphs as pointer assertions.This paper studies the equivalence theory and implication theory of shape graphs,as well as their decision procedures and applications.First,we investigate the shape graph theory using analogous methods to those in studying the theory of algebraic specification, where shape graphs and their equivalence rules and implication rules are analogous to algebraic terms and their equality rules and rewriting rules,respectively.Analogously,we define the syntactic theory and semantic theory of shape graphs,and then define the shape graph rewriting system as well as its termination,local confluence and confluence.Based on these definitions,we present decision methods on deciding the equality and implication of shape graphs by rewriting shape graphs.Secondly,we propose methods for automatically inferring loop-invariant shape graphs as well as the pre-and post-shape graphs of recursive functions.With the help of the decision procedures for the shape graph theory,the proposed method for inferring loop-invariant shape graphs has been adapted from a general method for inferring loop invariants based on abstract interpretation.Since a terminal recursive function has at least one non-recursive exit,the initial post-shape graphs of the function can be inferred along the non-recursive path,and then post-shape graphs can be iteratively inferred along the recursive paths.Accordingly,the pre-and post-shape graphs of recursive functions can be inferred like the method inferring loop-invariant shape graphs.Thirdly,by referencing the Nelson-Oppen combination method,we propose a decision method for the combination of the theory of shape graphs and integer theory.For mutable data structures,in addition to caring about whether nodes of a data structure form the predetermined shape,features such as data arrangement between nodes are also cared.Such features cannot be divorced from the shape feature of mutable data structures,and cannot be verified alone.Therefore,according to the characteristics of verification conditions generated from such programs,the proposed combination method uses shape graphs obtained from program analysis to group symbolic assertions by shape graph nodes;then uses integer theory to infer as many properties as possible for the nodes;and finally passes the grouped assertions and properties to the Z3 theorem prover for automatic verification.This method can effectively avoid failures to prove verification conditions.Based on the shape graph theory and the work of this paper,our prototype of program verification system alleviates the burden of automated theorem provers,and can verify programs manipulating more complex mutable data structures,such as insert functions and delete functions of sorted circular doubly linked list,binary search tree,splay tree,treap, balanced binary tree and AA tree. Keywords shape graph logic;shape analysis;program verification;automated theorem proving; loop-invariant inference 全攸关嵌入式软件的测试.和单元测试相比,单元证 1 引 言 明降低了投入,主要是因为它方便了维护山.演绎验 证在工业界的应用虽有限但也在拓展,达索航空公 形式验证(包括抽象解释、模型检测和演绎验证 司在健壮性的形式验证方面,已有约15%的断言是 等途径)是提高软件可信程度的重要方法,并在工业 用演绎验证方式证明的叮 界已经逐步得到应用,尤其是抽象解释和模型检测. 在演绎验证方法中,有关自动程序验证的大部 例如,空客公司在A400M军用运输机以及A380和 分研究按这样的途径开展:程序员提供函数前后条 A350客机的开发上,已经用形式验证取代了部分安 件和循环不变式,系统对程序采用某种正向或逆向
arealiasesornot.TheshapegraphlogicisanextensiontoHoarelogic,whichdirectlyusesshape graphsaspointerassertions.Thispaperstudiestheequivalencetheoryandimplicationtheoryof shapegraphs,aswellastheirdecisionproceduresandapplications.First,weinvestigatethe shapegraphtheoryusinganalogousmethodstothoseinstudyingthetheoryofalgebraicspecification, whereshapegraphsandtheirequivalencerulesandimplicationrulesareanalogoustoalgebraic termsandtheirequalityrulesandrewritingrules,respectively.Analogously,wedefinethe syntactictheoryandsemantictheoryofshapegraphs,andthendefinetheshapegraphrewriting systemaswellasitstermination,localconfluenceandconfluence.Basedonthesedefinitions,we presentdecisionmethodsondecidingtheequalityandimplicationofshapegraphsbyrewriting shapegraphs.Secondly,weproposemethodsforautomaticallyinferringloopinvariantshape graphsaswellasthepreandpostshapegraphsofrecursivefunctions.Withthehelpofthe decisionproceduresfortheshapegraphtheory,theproposedmethodforinferringloopinvariant shapegraphshasbeenadaptedfromageneralmethodforinferringloopinvariantsbasedon abstractinterpretation.Sinceaterminalrecursivefunctionhasatleastonenonrecursiveexit,the initialpostshapegraphsofthefunctioncanbeinferredalongthenonrecursivepath,andthen postshapegraphscanbeiterativelyinferredalongtherecursivepaths.Accordingly,thepreand postshapegraphsofrecursivefunctionscanbeinferredlikethemethodinferringloopinvariant shapegraphs.Thirdly,byreferencingtheNelsonOppencombinationmethod,weproposea decisionmethodforthecombinationofthetheoryofshapegraphsandintegertheory.For mutabledatastructures,inadditiontocaringaboutwhethernodesofadatastructureformthe predeterminedshape,featuressuchasdataarrangementbetweennodesarealsocared.Such featurescannotbedivorcedfromtheshapefeatureofmutabledatastructures,andcannotbe verifiedalone.Therefore,accordingtothecharacteristicsofverificationconditionsgenerated fromsuchprograms,theproposedcombinationmethodusesshapegraphsobtainedfromprogram analysistogroupsymbolicassertionsbyshapegraphnodes;thenusesintegertheorytoinferas manypropertiesaspossibleforthenodes;andfinallypassesthegroupedassertionsandpropertiesto theZ3theoremproverforautomaticverification.Thismethodcaneffectivelyavoidfailuresto proveverificationconditions.Basedontheshapegraphtheoryandtheworkofthispaper,our prototypeofprogramverificationsystemalleviatestheburdenofautomatedtheoremprovers,and canverifyprogramsmanipulatingmorecomplexmutabledatastructures,suchasinsertfunctions anddeletefunctionsofsortedcirculardoublylinkedlist,binarysearchtree,splaytree,treap, balancedbinarytreeandAAtree. 犓犲狔狑狅狉犱狊shapegraphlogic;shapeanalysis;programverification;automatedtheoremproving; loopinvariantinference 1引言 形式验证(包括抽象解释、模型检测和演绎验证 等途径)是提高软件可信程度的重要方法,并在工业 界已经逐步得到应用,尤其是抽象解释和模型检测. 例如,空客公司在A400M军用运输机以及A380和 A350客机的开发上,已经用形式验证取代了部分安 全攸关嵌入式软件的测试.和单元测试相比,单元证 明降低了投入,主要是因为它方便了维护[1].演绎验 证在工业界的应用虽有限但也在拓展,达索航空公 司在健壮性的形式验证方面,已有约15%的断言是 用演绎验证方式证明的[1]. 在演绎验证方法中,有关自动程序验证的大部 分研究按这样的途径开展:程序员提供函数前后条 件和循环不变式,系统对程序采用某种正向或逆向 12期 张昱等:形状图理论的定理证明 2461

2462 计算 龙 学 报 2016年 的演算来产生验证条件(即把对程序满足某些性质 理论.例如,对于用根节点的中序前驱(其左子树中 的证明转化为对一些验证条件的证明),然后用自动 最右下的节点)代替根节点的、删除二叉排序树根节 定理证明器来证明验证条件,如Ynot)、Spec#[ 点的函数,若要证明结果仍然是二叉排序树,则需要 和ESC/Java).有些研究依靠符号计算及其过程中 用到二叉排序树的两个性质:左子树中任何节点的 的定理证明来避免验证条件的生成,如smallfoot) 值一定小于右子树中各节点的值,左子树中最右下 和jStar6].无论用哪种策略,演绎验证方法都使用 节点的值大于左子树中其他节点的任何值.它们都 严谨的方式对软件系统进行数学推理,并且都借助 是二叉排序树的归纳性质,但是基于演绎推理的自 定理证明软件,如定理证明器Isabelle/HOL)、定 动定理证明器不可能从二叉排序树的归纳定义推导 理证明辅助工具Cog①、SMT(Satisfiability Modulo 出这些性质,因而无法证明依赖这些性质的验证 Theories)求解器Z3[s]. 条件 基于演绎推理的自动形式验证方法对自动定理 为验证操作易变数据结构的指针程序,我们提 证明器的能力有较高期待.首先,定理证明器在程序 出了形状图逻辑].形状图是描述程序所操作的静 验证过程中频繁使用.大到验证条件的证明和循环 态声明的指针型变量(简称声明指针)和动态分配的 不变式的推断,小到下标变量的别名判断和数组边 结构体中指针型域变量(简称域指针)的指向的一种 界检查,都需要或可以使用定理证明器.其次,需要 有向图.它准确表达了指针的有效性(指针有效是说 能够应对各种领域专用逻辑的定理证明.应用程序 该指针指向已分配且尚未释放的内存块)和指针的 的代码中可能涉及多种数据类型,操作系统的代码 相等性,因而可作为指针程序中指针有效性和相等 依赖于硬件特性,为完成对这些程序的验证,需要定 性的断言.形状图逻辑就是一种直接把形状图作为 理证明器能够覆盖这些领域专用逻辑的定理证明. 程序中指针断言集的程序逻辑.它是Hoare逻辑的 第三,需要定理证明器能处理各种理论的组合.例如 一种扩展,为指针操作语句设计了专门的推理规则, 面向数组类型的数组逻辑,它由下标逻辑和元素逻 这些规则用图形方式描述指针操作语句引起的形状 辑组成.对于操作数组的程序的验证,定理证明器要 图上被关注部分的变化.利用形状图还可以方便地 能证明这两种逻辑的相应理论(可能还包括等式理 消除访问路径别名,使易变数据结构上数据性质的 论和未解释函数理论)组合后形成的组合理论上的 验证仍可用Hoare逻辑的规则进行推理 定理.组合理论的问题复杂性在于:即使两个理论分 本文补足文献[10]所缺少的部分理论和算法 别可判定,其组合理论未必可判定[).数组理论就是 文献[10]主要围绕程序逻辑层面,提出把形状图作 这样的例子 为指针断言,并在此基础上设计了推理指针程序的 本文研究操作易变数据结构(包括单/双向链 形状图逻辑和检查形状合法性的形状系统.本文围 表、循环单/双向链表②和二叉链表示的二叉树)的 绕作为指针断言的形状图,研究形状图的等价理论 指针程序的自动验证中的一些定理证明问题.这类 和蕴涵理论以及它们的判定方法和应用.本文的贡 程序的验证非常困难.首先,难以给出表达程序性质 献有如下3点: 的函数前后条件,尤其是循环不变式.因为它们涉及 (1)提出形状图理论的一种判定方法。 所操作的数据结构的结构性质(常使用带量词的命 本文把形状图及其等价规则和蕴涵规则分别类 题和可达性谓词来表达)以及在数据结构中各节点 比为代数项及其等式规则和重写规则,像研究代数 内的数据的性质,而后者的描述可能紧密依赖于数 规范的理论那样来研究形状图理论,本文类似地定 据结构的结构性质,例如平衡二叉树节点的平衡因 义形状图的语法理论和语义理论,定义形状图重 子和AA树节点的level值.其次,难以证明这类程 写系统及其终止性、局部合流性和合流性,最后得到 序的验证条件,因为在验证条件中经常出现对数据 基于形状图重写的形状图等价判定和蕴涵判定的 结构所有节点的某种全称量化,这导致不能使用像 方法。 Nelson-(Oppen框架[]这样仅适用于无量词理论的 (2)提出循环不变形状图和递归函数前后形状 传统的理论组合.Z3虽然通过使用E-graph匹配技 术能够处理量化公式,但也难以适应复杂的量化公 D The Cog Development Team.The Cog proof assistant reference 式.除了要用量词刻画性质以及涉及的理论组合之 manual (Version 8.2),2009.URL http://cog.inria.fr ②本文用“单/双向链表”表示非循环的单/双向链表,用“(循 外,验证条件的证明可能还要用到数据结构的归纳 环)单/双向链表”表示循环和/或非循环的单/双向链表
的演算来产生验证条件(即把对程序满足某些性质 的证明转化为对一些验证条件的证明),然后用自动 定理证明器来证明验证条件,如Ynot[2]、Spec#[3] 和ESC/Java[4].有些研究依靠符号计算及其过程中 的定理证明来避免验证条件的生成,如smallfoot[5] 和jStar[6].无论用哪种策略,演绎验证方法都使用 严谨的方式对软件系统进行数学推理,并且都借助 定理证明软件,如定理证明器Isabelle/HOL[7]、定 理证明辅助工具Coq①、SMT(SatisfiabilityModulo Theories)求解器Z3[8]. 基于演绎推理的自动形式验证方法对自动定理 证明器的能力有较高期待.首先,定理证明器在程序 验证过程中频繁使用.大到验证条件的证明和循环 不变式的推断,小到下标变量的别名判断和数组边 界检查,都需要或可以使用定理证明器.其次,需要 能够应对各种领域专用逻辑的定理证明.应用程序 的代码中可能涉及多种数据类型,操作系统的代码 依赖于硬件特性,为完成对这些程序的验证,需要定 理证明器能够覆盖这些领域专用逻辑的定理证明. 第三,需要定理证明器能处理各种理论的组合.例如 面向数组类型的数组逻辑,它由下标逻辑和元素逻 辑组成.对于操作数组的程序的验证,定理证明器要 能证明这两种逻辑的相应理论(可能还包括等式理 论和未解释函数理论)组合后形成的组合理论上的 定理.组合理论的问题复杂性在于:即使两个理论分 别可判定,其组合理论未必可判定[9].数组理论就是 这样的例子. 本文研究操作易变数据结构(包括单/双向链 表、循环单/双向链表②和二叉链表示的二叉树)的 指针程序的自动验证中的一些定理证明问题.这类 程序的验证非常困难.首先,难以给出表达程序性质 的函数前后条件,尤其是循环不变式.因为它们涉及 所操作的数据结构的结构性质(常使用带量词的命 题和可达性谓词来表达)以及在数据结构中各节点 内的数据的性质,而后者的描述可能紧密依赖于数 据结构的结构性质,例如平衡二叉树节点的平衡因 子和AA树节点的level值.其次,难以证明这类程 序的验证条件,因为在验证条件中经常出现对数据 结构所有节点的某种全称量化.这导致不能使用像 NelsonOppen框架[9]这样仅适用于无量词理论的 传统的理论组合.Z3虽然通过使用Egraph匹配技 术能够处理量化公式,但也难以适应复杂的量化公 式.除了要用量词刻画性质以及涉及的理论组合之 外,验证条件的证明可能还要用到数据结构的归纳 理论.例如,对于用根节点的中序前驱(其左子树中 最右下的节点)代替根节点的、删除二叉排序树根节 点的函数,若要证明结果仍然是二叉排序树,则需要 用到二叉排序树的两个性质:左子树中任何节点的 值一定小于右子树中各节点的值,左子树中最右下 节点的值大于左子树中其他节点的任何值.它们都 是二叉排序树的归纳性质,但是基于演绎推理的自 动定理证明器不可能从二叉排序树的归纳定义推导 出这些性质,因而无法证明依赖这些性质的验证 条件.为验证操作易变数据结构的指针程序,我们提 出了形状图逻辑[10].形状图是描述程序所操作的静 态声明的指针型变量(简称声明指针)和动态分配的 结构体中指针型域变量(简称域指针)的指向的一种 有向图.它准确表达了指针的有效性(指针有效是说 该指针指向已分配且尚未释放的内存块)和指针的 相等性,因而可作为指针程序中指针有效性和相等 性的断言.形状图逻辑就是一种直接把形状图作为 程序中指针断言集的程序逻辑.它是Hoare逻辑的 一种扩展,为指针操作语句设计了专门的推理规则, 这些规则用图形方式描述指针操作语句引起的形状 图上被关注部分的变化.利用形状图还可以方便地 消除访问路径别名,使易变数据结构上数据性质的 验证仍可用Hoare逻辑的规则进行推理. 本文补足文献[10]所缺少的部分理论和算法. 文献[10]主要围绕程序逻辑层面,提出把形状图作 为指针断言,并在此基础上设计了推理指针程序的 形状图逻辑和检查形状合法性的形状系统.本文围 绕作为指针断言的形状图,研究形状图的等价理论 和蕴涵理论以及它们的判定方法和应用.本文的贡 献有如下3点: (1)提出形状图理论的一种判定方法. 本文把形状图及其等价规则和蕴涵规则分别类 比为代数项及其等式规则和重写规则,像研究代数 规范的理论那样来研究形状图理论.本文类似地定 义形状图的语法理论和语义理论,定义形状图重 写系统及其终止性、局部合流性和合流性,最后得到 基于形状图重写的形状图等价判定和蕴涵判定的 方法.(2)提出循环不变形状图和递归函数前后形状 2462 计 算 机 学 报 2016年 ① ② TheCoqDevelopmentTeam.TheCoqproofassistantreference manual(Version8.2),2009.URLhttp://coq.inria.fr 本文用“单/双向链表”表示非循环的单/双向链表,用“(循 环)单/双向链表”表示循环和/或非循环的单/双向链表.

12期 张昱等:形状图理论的定理证明 2463 图的自动推断算法 还可能有与浓缩节点含义一致的表达式e和断言 借助形状图理论的判定方法,本文把一个通过 a.指向谓词节点的有向边以及该节点下侧的e和a 迭代推断循环不变式的一般方法]改编成一个推 是该节点所代表的谓词的变元,例如图2给出了几 断循环不变形状图的方法;进一步设计该方法的一 种用形状图定义的数据结构,以单链表为例,图中谓 个变种来迭代推断递归函数的前后形状图. 词节点的变元和左侧的符号谓词1ist(s,e,a)的变元 (3)提出形状图理论和整数理论组合的一种判 是一致的. 定方法 单链表 对易变数据结构,除了关心数据结构各节点是 list(s,e,a) 否连成预定的形状外,往往还关心数据在这些节点 list,e.a 0.3 间的排列特性,它们不能脱离易变数据结构的结构 双向链表 dlist(s.e,a) GG网 特点而单独验证.于是需要研究形状图理论和整数 dlist,e,a 上线性算术理论(假定节点数据是整型)组合的判定 a→(e==0) 问题.本文针对验证条件的特点,利用程序分析阶段 得到的形状图,参照Nelson-(Oppen框架,提出形状 图理论和整数上线性算术理论组合的一种判定方法 网 dlist.e. a→(e>= 本文第2节简要回顾文献[10]提出的形状图、 形状图变换规则和形状图逻辑;第3节介绍形状图 双向链表 dlist(s 理论的判定方法;第4节介绍循环不变形状图的推 dlist 断和递归函数前后形状图的推断:第5节介绍形状 图理论和整数理论组合的判定方法:第6节是验证 实例:第7节是和相关研究工作的比较:第8节是 ©89图 总结 二叉树 tree(s) 2 形状图和形状图逻辑 o o-B 2.1形状图 形状图是描述程序中静态声明指针和动态分配 图2形状谓词定义的一些例子 的结构体中域指针的指向关系的一种有向图, 形状图的顶点(也称节点)有6种,其图形化语 形状图中的有向边表示声明指针和域指针的指 法形式见图1.其中声明节点和结构节点分别表示 向,指向同一个节点(悬空节点除外)的指针相等.有 静态声明指针和动态分配的结构体.null节点和悬 向边及其连接的节点满足如下语法约束: 空节点的用意稍后会提到 (1)声明节点.只有唯一的出边,没有入边,出 边的标记就是声明指针名. D i (2)结构节点和浓缩节点.有入边和出边,其中 声明节点结构节点u节点悬空节点ea 浓缩节点 name,e,a 调词节点 出边的条数与结构节点所代表的结构体的域指针个 图1形状图的各种节点 数一致,各出边的标记分别是各域指针名。 浓缩节点是若干个结构节点和它们之间的有向 (3)ull节点、悬空节点和谓词节点.有入边,没 边的浓缩表示,其灰色矩形下侧的表达式e和断言 有出边.ul节点和悬空节点分别用来表示指向它 a分别表示被浓缩的结构节点的个数以及对e的取 们的有向边代表null指针和悬空指针. 值范围的约束,若灰色矩形下无e和a,称为无约束 形状图的定义:(1)节点和有向边满足上述语 浓缩节点,它表示被浓缩的结构节点个数任意,可以 法约束,各声明节点出边标记相异,且边被视为无向 是0个 时则连通的图形是形状图;(2)若形状图G1,G2,…, 谓词节点代表满足指定谓词的若干节点和它们 G.的声明节点出边标记集两两相交都为空,则由逻 之间的有向边,其矩形节点下侧标有谓词名name, 辑合取符号∧连接的G1∧G2∧…∧Gm也是形状图
图的自动推断算法. 借助形状图理论的判定方法,本文把一个通过 迭代推断循环不变式的一般方法[11]改编成一个推 断循环不变形状图的方法;进一步设计该方法的一 个变种来迭代推断递归函数的前后形状图. (3)提出形状图理论和整数理论组合的一种判 定方法.对易变数据结构,除了关心数据结构各节点是 否连成预定的形状外,往往还关心数据在这些节点 间的排列特性,它们不能脱离易变数据结构的结构 特点而单独验证.于是需要研究形状图理论和整数 上线性算术理论(假定节点数据是整型)组合的判定 问题.本文针对验证条件的特点,利用程序分析阶段 得到的形状图,参照NelsonOppen框架,提出形状 图理论和整数上线性算术理论组合的一种判定方法. 本文第2节简要回顾文献[10]提出的形状图、 形状图变换规则和形状图逻辑;第3节介绍形状图 理论的判定方法;第4节介绍循环不变形状图的推 断和递归函数前后形状图的推断;第5节介绍形状 图理论和整数理论组合的判定方法;第6节是验证 实例;第7节是和相关研究工作的比较;第8节是 总结. 2形状图和形状图逻辑 21形状图 形状图是描述程序中静态声明指针和动态分配 的结构体中域指针的指向关系的一种有向图. 形状图的顶点(也称节点)有6种,其图形化语 法形式见图1.其中声明节点和结构节点分别表示 静态声明指针和动态分配的结构体.null节点和悬 空节点的用意稍后会提到. 图1形状图的各种节点 浓缩节点是若干个结构节点和它们之间的有向 边的浓缩表示,其灰色矩形下侧的表达式e和断言 a分别表示被浓缩的结构节点的个数以及对e的取 值范围的约束.若灰色矩形下无e和a,称为无约束 浓缩节点,它表示被浓缩的结构节点个数任意,可以 是0个.谓词节点代表满足指定谓词的若干节点和它们 之间的有向边,其矩形节点下侧标有谓词名name, 还可能有与浓缩节点含义一致的表达式e和断言 a.指向谓词节点的有向边以及该节点下侧的e和a 是该节点所代表的谓词的变元,例如图2给出了几 种用形状图定义的数据结构,以单链表为例,图中谓 词节点的变元和左侧的符号谓词list(s,e,a)的变元 是一致的. 图2形状谓词定义的一些例子 形状图中的有向边表示声明指针和域指针的指 向,指向同一个节点(悬空节点除外)的指针相等.有 向边及其连接的节点满足如下语法约束: (1)声明节点.只有唯一的出边,没有入边,出 边的标记就是声明指针名. (2)结构节点和浓缩节点.有入边和出边,其中 出边的条数与结构节点所代表的结构体的域指针个 数一致,各出边的标记分别是各域指针名. (3)null节点、悬空节点和谓词节点.有入边,没 有出边.null节点和悬空节点分别用来表示指向它 们的有向边代表null指针和悬空指针. 形状图的定义:(1)节点和有向边满足上述语 法约束,各声明节点出边标记相异,且边被视为无向 时则连通的图形是形状图;(2)若形状图犌1,犌2,…, 犌狀的声明节点出边标记集两两相交都为空,则由逻 辑合取符号∧连接的犌1∧犌2∧…∧犌狀也是形状图. 12期 张昱等:形状图理论的定理证明 2463
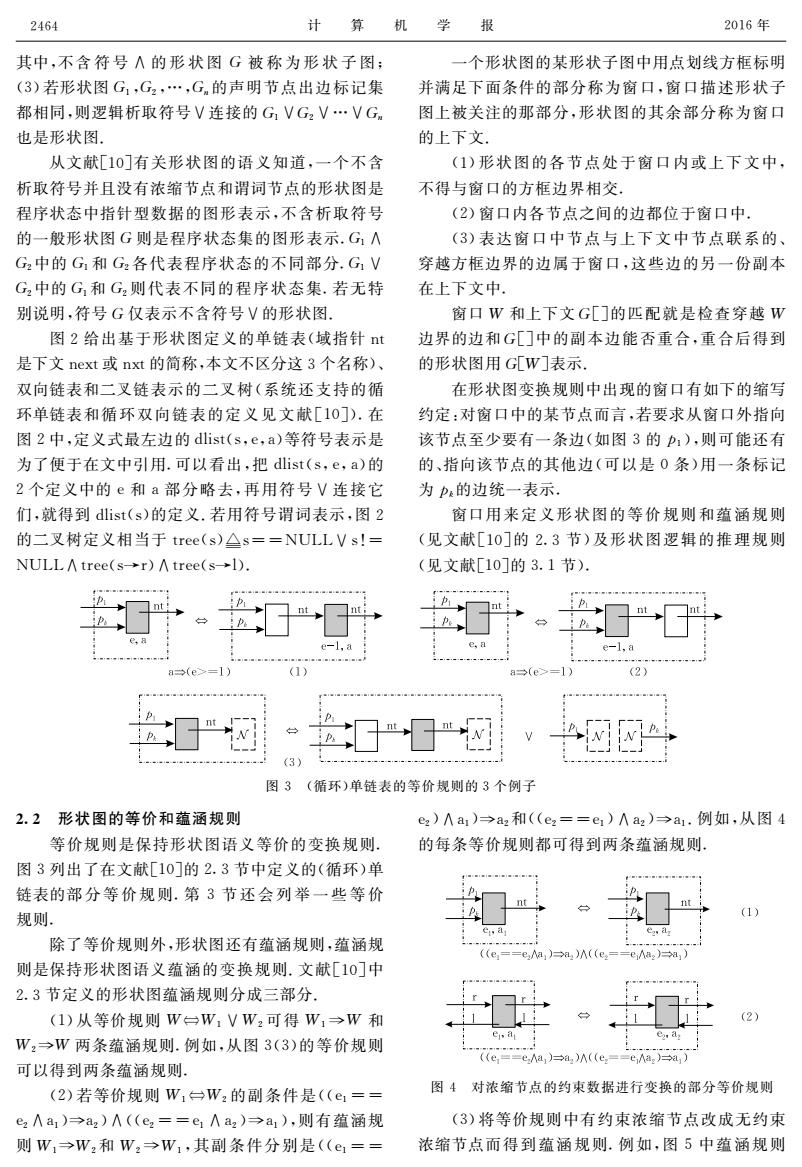
2464 计算 学 报 2016年 其中,不含符号八的形状图G被称为形状子图; 一个形状图的某形状子图中用点划线方框标明 (3)若形状图G1,G2,…,Gn的声明节点出边标记集 并满足下面条件的部分称为窗口,窗口描述形状子 都相同,则逻辑析取符号V连接的G1VG2V…VGn 图上被关注的那部分,形状图的其余部分称为窗口 也是形状图」 的上下文 从文献[10]有关形状图的语义知道,一个不含 (1)形状图的各节点处于窗口内或上下文中, 析取符号并且没有浓缩节点和谓词节点的形状图是 不得与窗口的方框边界相交。 程序状态中指针型数据的图形表示,不含析取符号 (2)窗口内各节点之间的边都位于窗口中. 的一般形状图G则是程序状态集的图形表示.G1∧ (3)表达窗口中节点与上下文中节点联系的、 G2中的G和G2各代表程序状态的不同部分,G1V 穿越方框边界的边属于窗口,这些边的另一份副本 G2中的G和G2则代表不同的程序状态集.若无特 在上下文中。 别说明,符号G仅表示不含符号V的形状图, 窗口W和上下文G[]的匹配就是检查穿越W 图2给出基于形状图定义的单链表(域指针t 边界的边和G[]中的副本边能否重合,重合后得到 是下文next或nxt的简称,本文不区分这3个名称)、 的形状图用G[W]表示. 双向链表和二叉链表示的二叉树(系统还支持的循 在形状图变换规则中出现的窗口有如下的缩写 环单链表和循环双向链表的定义见文献[10]).在 约定:对窗口中的某节点而言,若要求从窗口外指向 图2中,定义式最左边的dlist(s,e,a)等符号表示是 该节点至少要有一条边(如图3的p:),则可能还有 为了便于在文中引用.可以看出,把dlist(s,e,a)的 的、指向该节点的其他边(可以是0条)用一条标记 2个定义中的e和a部分略去,再用符号V连接它 为p的边统一表示。 们,就得到dist(s)的定义.若用符号谓词表示,图2 窗口用来定义形状图的等价规则和蕴涵规则 的二叉树定义相当于tree(s)△s==NULLVs!= (见文献[10]的2.3节)及形状图逻辑的推理规则 NULL∧tree(s→r)∧tree(s→-l) (见文献[10]的3.1节) e,a (1) a→(e>=1) (2) (3) 图3(循环)单链表的等价规则的3个例子 2.2形状图的等价和蕴涵规则 e)八a)→az和(e2==e1)∧az)→a1.例如,从图4 等价规则是保持形状图语义等价的变换规则. 的每条等价规则都可得到两条蕴涵规则, 图3列出了在文献[10]的2.3节中定义的(循环)单 链表的部分等价规则.第3节还会列举一些等价 nt 规则. (1) 除了等价规则外,形状图还有蕴涵规则,蕴涵规 ((e==ea1)→a)A((e2==eMa2)→a1) 则是保持形状图语义蕴涵的变换规则.文献[10]中 2.3节定义的形状图蕴涵规则分成三部分. (1)从等价规则W台W:VWz可得W1→W和 Wz→W两条蕴涵规则.例如,从图3(3)的等价规则 (e==eAa1)=a)A((e==eAa2)=→a1】 可以得到两条蕴涵规则. (2)若等价规则W1台W2的副条件是((e1== 图4对浓缩节点的约束数据进行变换的部分等价规则 e2Aa1)→az)∧((e2==e1∧a2)→a1),则有蕴涵规 (3)将等价规则中有约束浓缩节点改成无约束 则W,→W2和W2→W1,其副条件分别是(e1== 浓缩节点而得到蕴涵规则.例如,图5中蕴涵规则
其中,不含符号∧的形状图犌被称为形状子图; (3)若形状图犌1,犌2,…,犌狀的声明节点出边标记集 都相同,则逻辑析取符号∨连接的犌1∨犌2∨…∨犌狀 也是形状图. 从文献[10]有关形状图的语义知道,一个不含 析取符号并且没有浓缩节点和谓词节点的形状图是 程序状态中指针型数据的图形表示,不含析取符号 的一般形状图犌则是程序状态集的图形表示.犌1∧ 犌2中的犌1和犌2各代表程序状态的不同部分.犌1∨ 犌2中的犌1和犌2则代表不同的程序状态集.若无特 别说明,符号犌仅表示不含符号∨的形状图. 图2给出基于形状图定义的单链表(域指针nt 是下文next或nxt的简称,本文不区分这3个名称)、 双向链表和二叉链表示的二叉树(系统还支持的循 环单链表和循环双向链表的定义见文献[10]).在 图2中,定义式最左边的dlist(s,e,a)等符号表示是 为了便于在文中引用.可以看出,把dlist(s,e,a)的 2个定义中的e和a部分略去,再用符号∨连接它 们,就得到dlist(s)的定义.若用符号谓词表示,图2 的二叉树定义相当于tree(s)s==NULL∨s!= NULL∧tree(s→r)∧tree(s→l). 一个形状图的某形状子图中用点划线方框标明 并满足下面条件的部分称为窗口,窗口描述形状子 图上被关注的那部分,形状图的其余部分称为窗口 的上下文.(1)形状图的各节点处于窗口内或上下文中, 不得与窗口的方框边界相交. (2)窗口内各节点之间的边都位于窗口中. (3)表达窗口中节点与上下文中节点联系的、 穿越方框边界的边属于窗口,这些边的另一份副本 在上下文中. 窗口犠和上下文犌[]的匹配就是检查穿越犠 边界的边和犌[]中的副本边能否重合,重合后得到 的形状图用犌[犠]表示. 在形状图变换规则中出现的窗口有如下的缩写 约定:对窗口中的某节点而言,若要求从窗口外指向 该节点至少要有一条边(如图3的狆1),则可能还有 的、指向该节点的其他边(可以是0条)用一条标记 为狆犽的边统一表示. 窗口用来定义形状图的等价规则和蕴涵规则 (见文献[10]的2.3节)及形状图逻辑的推理规则 (见文献[10]的3.1节). 图3(循环)单链表的等价规则的3个例子 22形状图的等价和蕴涵规则 等价规则是保持形状图语义等价的变换规则. 图3列出了在文献[10]的2.3节中定义的(循环)单 链表的部分等价规则.第3节还会列举一些等价 规则.除了等价规则外,形状图还有蕴涵规则,蕴涵规 则是保持形状图语义蕴涵的变换规则.文献[10]中 2.3节定义的形状图蕴涵规则分成三部分. (1)从等价规则犠犠1∨犠2可得犠1犠和 犠2犠两条蕴涵规则.例如,从图3(3)的等价规则 可以得到两条蕴涵规则. (2)若等价规则犠1犠2的副条件是((e1== e2∧a1)a2)∧((e2==e1∧a2)a1),则有蕴涵规 则犠1犠2和犠2犠1,其副条件分别是((e1== e2)∧a1)a2和((e2==e1)∧a2)a1.例如,从图4 的每条等价规则都可得到两条蕴涵规则. 图4对浓缩节点的约束数据进行变换的部分等价规则 (3)将等价规则中有约束浓缩节点改成无约束 浓缩节点而得到蕴涵规则.例如,图5中蕴涵规则 2464 计 算 机 学 报 2016年
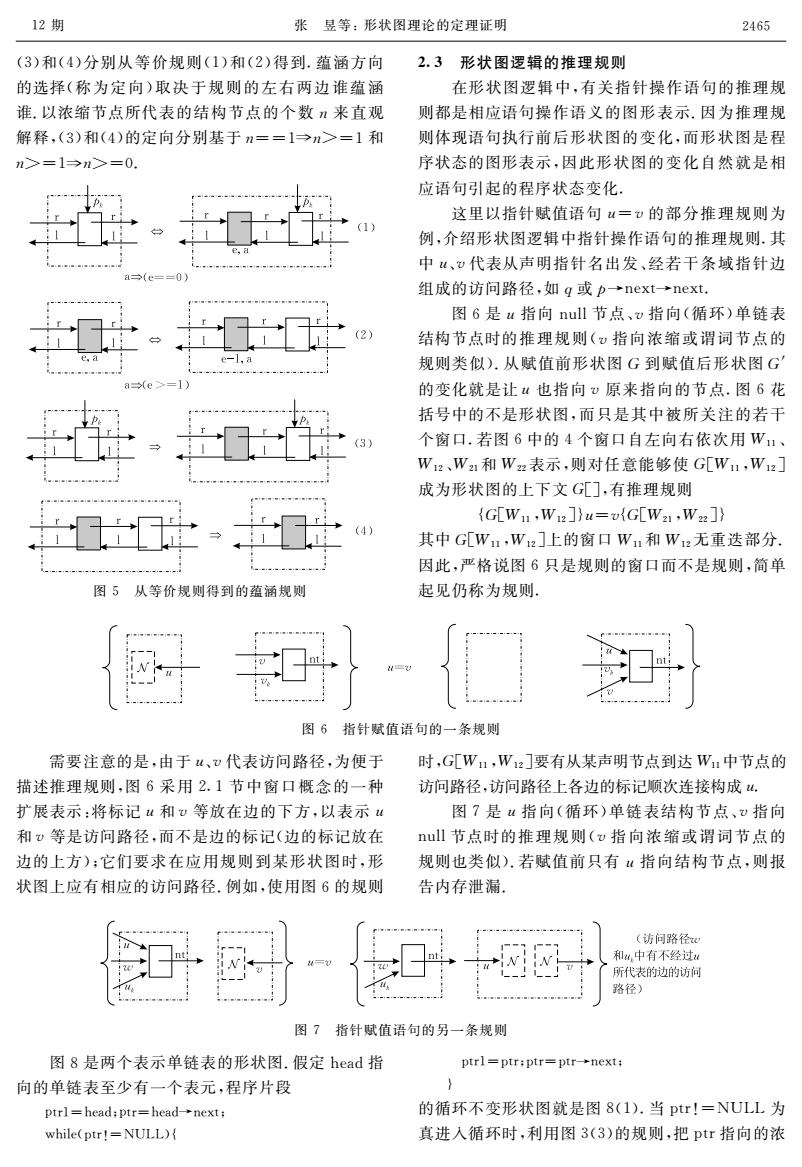
12期 张昱等:形状图理论的定理证明 2465 (3)和(4)分别从等价规则(1)和(2)得到.蕴涵方向 2.3形状图逻辑的推理规则 的选择(称为定向)取决于规则的左右两边谁蕴涵 在形状图逻辑中,有关指针操作语句的推理规 谁.以浓缩节点所代表的结构节点的个数n来直观 则都是相应语句操作语义的图形表示.因为推理规 解释,(3)和(4)的定向分别基于n==1→n>=1和 则体现语句执行前后形状图的变化,而形状图是程 n>=1→n>=0. 序状态的图形表示,因此形状图的变化自然就是相 应语句引起的程序状态变化. 这里以指针赋值语句u=?的部分推理规则为 1) 例,介绍形状图逻辑中指针操作语句的推理规则.其 中“、v代表从声明指针名出发、经若干条域指针边 组成的访问路径,如q或p→next->next. 图6是u指向null节点、v指向(循环)单链表 2) 结构节点时的推理规则(v指向浓缩或谓词节点的 规则类似).从赋值前形状图G到赋值后形状图G 的变化就是让也指向v原来指向的节点.图6花 括号中的不是形状图,而只是其中被所关注的若干 个窗口.若图6中的4个窗口自左向右依次用W1、 W2、W!和W2表示,则对任意能够使G[W11,W1z] 成为形状图的上下文G汇],有推理规则 {G[W1,W12]}u={G[W21,Wz2]} 其中G[W1,W2]上的窗口W1和W12无重迭部分。 因此,严格说图6只是规则的窗口而不是规则,简单 图5从等价规则得到的蕴规则 起见仍称为规则 图6指针赋值语句的一条规侧 需要注意的是,由于u、v代表访问路径,为便于 时,G[W1,W12]要有从某声明节点到达W,中节点的 描述推理规则,图6采用2.1节中窗口概念的一种 访问路径,访问路径上各边的标记顺次连接构成u. 扩展表示:将标记u和v等放在边的下方,以表示u 图7是“指向(循环)单链表结构节点、指向 和v等是访问路径,而不是边的标记(边的标记放在 null节点时的推理规则(v指向浓缩或谓词节点的 边的上方):它们要求在应用规则到某形状图时,形 规则也类似).若赋值前只有指向结构节点,则报 状图上应有相应的访问路径.例如,使用图6的规则 告内存泄漏, (访问路径 和4中有不经过u 所代表的边的访问 路径) 图7指针赋值语句的另一条规则 图8是两个表示单链表的形状图.假定head指 ptrl=ptr:ptr=ptr-next: 向的单链表至少有一个表元,程序片段 ptrl=head:ptr=head-next: 的循环不变形状图就是图8(1).当ptr!=NULL为 while(ptr!=NULL){ 真进入循环时,利用图3(3)的规则,把ptr指向的浓
(3)和(4)分别从等价规则(1)和(2)得到.蕴涵方向 的选择(称为定向)取决于规则的左右两边谁蕴涵 谁.以浓缩节点所代表的结构节点的个数狀来直观 解释,(3)和(4)的定向分别基于狀==1狀>=1和 狀>=1狀>=0. 图5从等价规则得到的蕴涵规则 23形状图逻辑的推理规则 在形状图逻辑中,有关指针操作语句的推理规 则都是相应语句操作语义的图形表示.因为推理规 则体现语句执行前后形状图的变化,而形状图是程 序状态的图形表示,因此形状图的变化自然就是相 应语句引起的程序状态变化. 这里以指针赋值语句狌=狏的部分推理规则为 例,介绍形状图逻辑中指针操作语句的推理规则.其 中狌、狏代表从声明指针名出发、经若干条域指针边 组成的访问路径,如狇或狆→next→next. 图6是狌指向null节点、狏指向(循环)单链表 结构节点时的推理规则(狏指向浓缩或谓词节点的 规则类似).从赋值前形状图犌到赋值后形状图犌′ 的变化就是让狌也指向狏原来指向的节点.图6花 括号中的不是形状图,而只是其中被所关注的若干 个窗口.若图6中的4个窗口自左向右依次用犠11、 犠12、犠21和犠22表示,则对任意能够使犌[犠11,犠12] 成为形状图的上下文犌[],有推理规则 {犌[犠11,犠12]}狌=狏{犌[犠21,犠22]} 其中犌[犠11,犠12]上的窗口犠11和犠12无重迭部分. 因此,严格说图6只是规则的窗口而不是规则,简单 起见仍称为规则. 图6指针赋值语句的一条规则 需要注意的是,由于狌、狏代表访问路径,为便于 描述推理规则,图6采用2.1节中窗口概念的一种 扩展表示:将标记狌和狏等放在边的下方,以表示狌 和狏等是访问路径,而不是边的标记(边的标记放在 边的上方);它们要求在应用规则到某形状图时,形 状图上应有相应的访问路径.例如,使用图6的规则 时,犌[犠11,犠12]要有从某声明节点到达犠11中节点的 访问路径,访问路径上各边的标记顺次连接构成狌. 图7是狌指向(循环)单链表结构节点、狏指向 null节点时的推理规则(狏指向浓缩或谓词节点的 规则也类似).若赋值前只有狌指向结构节点,则报 告内存泄漏. 图7指针赋值语句的另一条规则 图8是两个表示单链表的形状图.假定head指 向的单链表至少有一个表元,程序片段 ptr1=head;ptr=head→next; while(ptr!=NULL){ ptr1=ptr;ptr=ptr→next; } 的循环不变形状图就是图8(1).当ptr!=NULL为 真进入循环时,利用图3(3)的规则,把ptr指向的浓 12期 张昱等:形状图理论的定理证明 2465

2466 女 算 学 报 2016年 缩节点展开成两种情况,其一与ptr!=NULL矛 形状图等价规则限制为单向后得到的蕴涵规则 盾被略去,另一种情况就是图8(2)的形状图.把语 就是一条形状图重写规则.一组形状图重写规则构 句ptrl=ptr当作语句序列dummy=ptr;ptrl= 成一个形状图重写系统.不能用该系统的规则再进 NULL:ptrl=dummy:dummy=NULL,按图6和 行归约的形状图称为最简形状图.不存在无穷归约 图7的规则逐步修改图8(2),其中dummy是初值 序列的系统称为具有终止性的系统.可以参照项重 为NULL的虚拟局部指针变量.引入dummy主要 写系统继续定义系统的临界对(critical pair)、局部 是为了避免为某些特殊的指针赋值情况设计复杂的 合流性和合流性, 专用规则,见文献[10]的3.1节.对ptr=ptr--next 仿照Knuth-Bendix完备化过程),可以把文 也继续用类似的方法修改形状图,再把得到的形状 献[10]中2.3节的等价规则集变换成一个与之等价 图用类似图3(3)的规则,把ptr1原先指向的结构节 并且终止与合流的形状图重写系统R 点逆向折叠进左边的浓缩节点,得到图8(1). 下面先以一个简单的项重写系统为例来熟悉项 重写系统的一些概念,然后说明项重写和形状图重 写之间的主要异同.例如,代数等式 x十0=x,x十(一x)=0,(x十y)十之=x十(y十) nex 是属于包含0、加和一元减的自然数等式系统中的 等式,把它们从左到右定向,得到3条重写规则 x+0→x,x+(-x)→0,(x+y)+2→x+(y+之) 项x+(y+(一y)的子项y+(一y)与第2条规则 的左部匹配,因此x十(y+(一y)可用第2条规则 重写成x十0,再依据第1条规则重写为x.不难证 (2) 明这3条规则构成的重写系统是终止的. 图8形状图的两个例子 要证明合流性,需要考察临界对.第3条规则左 部的子项x十y和该规则左部(x'+y)+之'(加撇号 3形状图理论的判定方法 以便区别)合一,得到临界对 ((x'+y')+(+),(x'+(y+之'))+》 形状图的等价推理规则集由文献[10]中2.3节的 该临界对中的两个项都能归约到x'十(y'十(z'十z)) 形状图等价规则(不包括那些推导形状图析取G1VG2 可以类似地计算该重写系统的其它临界对并证明每 的规则,例如本文图3(3))和任何等价推理系统都 一临界对中的两个项都能归约到同一个项,所以该 有的自反、对称和传递规则组成.该规则集可用来证 系统具有局部合流性,再由终止性可得该系统具有 明形状图之间的等价性, 合流性。 若等价形状图的集合E是封闭于可证明的,即 在上述项重写系统中,规则的左部和右部都是 项,被重写的也是项.而形状图系统与项重写系统相 G1台G2蕴涵G台G2∈£,则把£叫做形状图的一 比,最大的区别是:规则的左部和右部都是窗口,被 个语法等价理论.类似地可以定义形状图相应的语 重写的是形状图.产生该区别的根源在于形状图是 义等价理论,即=G台G2蕴涵G1台G2∈C.由文献 二维的.基于同样的原因,合一和匹配的描述也有区 [10]中2.4节关于等价规则的性质定理,不难证明 别.但是两个系统的本质概念和方法是一致的, £G1台G2当且仅当£=G,台G2.类似地根据形状图 下面先给出节点相同和形状图相同的定义 的蕴涵规则,可以定义形状图的语法蕴涵理论和语义 定义1.节点1和2若满足下面两个条件,则 蕴涵理论及证明G1→G2当且仅当卡G,→G2: 称m1和n2相同: 本节介绍形状图的重写系统和这两种理论的判 (1)1和2是同类节点,并且若都是声明节点、 定方法。 结构节点或浓缩节点,则有同样的出边及其标记;若 3.1形状图的等价重写系统 都是谓词节点,则谓词名相同. 形状图的等价重写系统可比照代数项的重写系 (2)若1和2是同类浓缩节点或谓词节点,且 统[]来讨论.它用于形状分析和验证过程中对形状 分别带e1与a1和e2与a2,则必须满足(e1==e2A 图进行等价化简. a1)→a2并且(e1==e2∧a2)→a1.其中,无约束浓缩
缩节点展开成两种情况,其一与ptr!=NULL矛 盾被略去,另一种情况就是图8(2)的形状图.把语 句ptr1=ptr当作语句序列dummy=ptr;ptr1= NULL;ptr1=dummy;dummy=NULL,按图6和 图7的规则逐步修改图8(2),其中dummy是初值 为NULL的虚拟局部指针变量.引入dummy主要 是为了避免为某些特殊的指针赋值情况设计复杂的 专用规则,见文献[10]的3.1节.对ptr=ptr→next 也继续用类似的方法修改形状图,再把得到的形状 图用类似图3(3)的规则,把ptr1原先指向的结构节 点逆向折叠进左边的浓缩节点,得到图8(1). 图8形状图的两个例子 3形状图理论的判定方法 形状图的等价推理规则集由文献[10]中2.3节的 形状图等价规则(不包括那些推导形状图析取犌1∨犌2 的规则,例如本文图3(3))和任何等价推理系统都 有的自反、对称和传递规则组成.该规则集可用来证 明形状图之间的等价性. 若等价形状图的集合犈是封闭于可证明的,即 ! "犌1犌2蕴涵犌1犌2∈!,则把!叫做形状图的一 个语法等价理论.类似地可以定义形状图相应的语 义等价理论,即! #犌1犌2蕴涵犌1犌2∈!.由文献 [10]中2.4节关于等价规则的性质定理,不难证明 ! "犌1犌2当且仅当! #犌1犌2.类似地根据形状图 的蕴涵规则,可以定义形状图的语法蕴涵理论和语义 蕴涵理论及证明! "犌1犌2当且仅当! #犌1犌2. 本节介绍形状图的重写系统和这两种理论的判 定方法. 31形状图的等价重写系统 形状图的等价重写系统可比照代数项的重写系 统[12]来讨论.它用于形状分析和验证过程中对形状 图进行等价化简. 形状图等价规则限制为单向后得到的蕴涵规则 就是一条形状图重写规则.一组形状图重写规则构 成一个形状图重写系统.不能用该系统的规则再进 行归约的形状图称为最简形状图.不存在无穷归约 序列的系统称为具有终止性的系统.可以参照项重 写系统继续定义系统的临界对(criticalpair)、局部 合流性和合流性. 仿照KnuthBendix完备化过程[13],可以把文 献[10]中2.3节的等价规则集变换成一个与之等价 并且终止与合流的形状图重写系统$. 下面先以一个简单的项重写系统为例来熟悉项 重写系统的一些概念,然后说明项重写和形状图重 写之间的主要异同.例如,代数等式 狓+0=狓,狓+(-狓)=0,(狓+狔)+狕=狓+(狔+狕) 是属于包含0、加和一元减的自然数等式系统中的 等式,把它们从左到右定向,得到3条重写规则 狓+0→狓,狓+(-狓)→0,(狓+狔)+狕→狓+(狔+狕) 项狓+(狔+(-狔))的子项狔+(-狔)与第2条规则 的左部匹配,因此狓+(狔+(-狔))可用第2条规则 重写成狓+0,再依据第1条规则重写为狓.不难证 明这3条规则构成的重写系统是终止的. 要证明合流性,需要考察临界对.第3条规则左 部的子项狓+狔和该规则左部(狓′+狔′)+狕′(加撇号 以便区别)合一,得到临界对 〈(狓′+狔′)+(狕′+狕),(狓′+(狔′+狕′))+狕〉 该临界对中的两个项都能归约到狓′+(狔′+(狕′+狕)). 可以类似地计算该重写系统的其它临界对并证明每 一临界对中的两个项都能归约到同一个项,所以该 系统具有局部合流性.再由终止性可得该系统具有 合流性.在上述项重写系统中,规则的左部和右部都是 项,被重写的也是项.而形状图系统与项重写系统相 比,最大的区别是:规则的左部和右部都是窗口,被 重写的是形状图.产生该区别的根源在于形状图是 二维的.基于同样的原因,合一和匹配的描述也有区 别.但是两个系统的本质概念和方法是一致的. 下面先给出节点相同和形状图相同的定义. 定义1.节点狀1和狀2若满足下面两个条件,则 称狀1和狀2相同: (1)狀1和狀2是同类节点,并且若都是声明节点、 结构节点或浓缩节点,则有同样的出边及其标记;若 都是谓词节点,则谓词名相同. (2)若狀1和狀2是同类浓缩节点或谓词节点,且 分别带e1与a1和e2与a2,则必须满足(e1==e2∧ a1)a2并且(e1==e2∧a2)a1.其中,无约束浓缩 2466 计 算 机 学 报 2016年
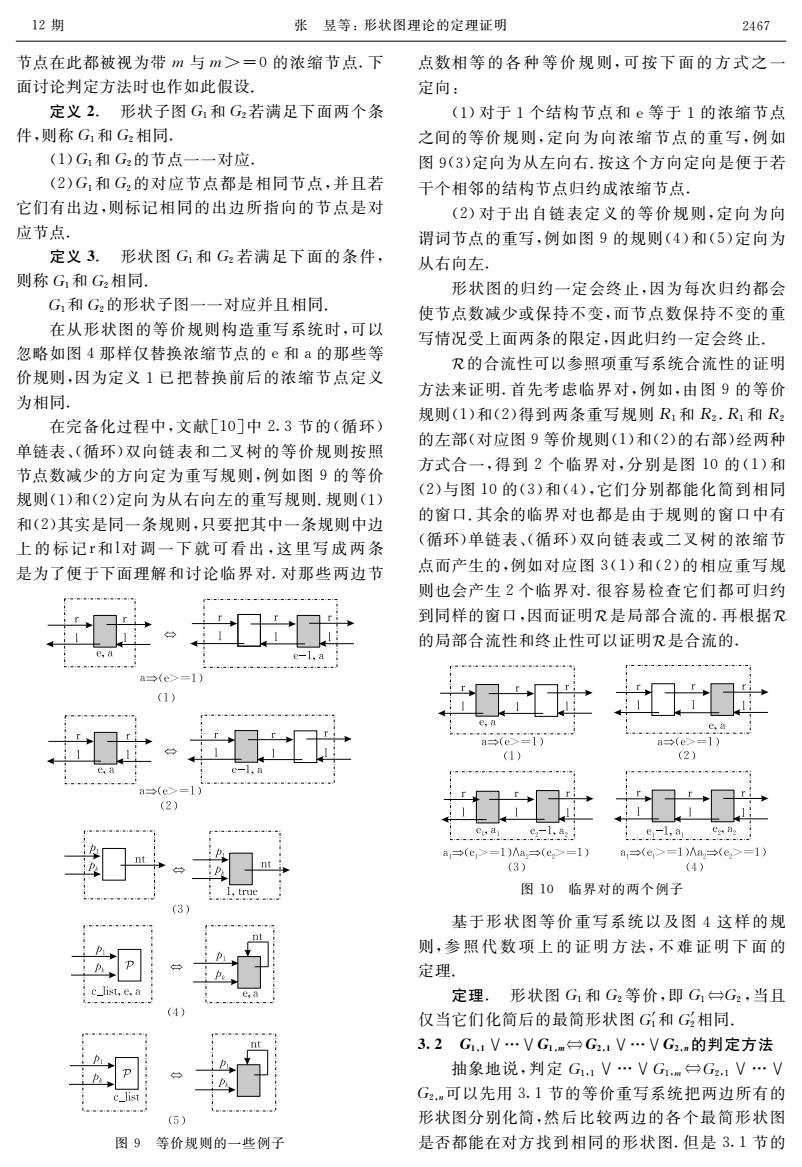
12期 张昱等:形状图理论的定理证明 2467 节点在此都被视为带m与m>=0的浓缩节点.下 点数相等的各种等价规则,可按下面的方式之一 面讨论判定方法时也作如此假设, 定向: 定义2.形状子图G1和G2若满足下面两个条 (1)对于1个结构节点和e等于1的浓缩节点 件,则称G1和G2相同. 之间的等价规则,定向为向浓缩节点的重写,例如 (1)G1和G2的节点一一对应。 图9(3)定向为从左向右.按这个方向定向是便于若 (2)G1和G2的对应节点都是相同节点,并且若 干个相邻的结构节点归约成浓缩节点· 它们有出边,则标记相同的出边所指向的节点是对 (2)对于出自链表定义的等价规则,定向为向 应节点。 谓词节点的重写,例如图9的规则(4)和(5)定向为 定义3.形状图G1和G2若满足下面的条件, 从右向左 则称G1和G2相同, 形状图的归约一定会终止,因为每次归约都会 G1和G2的形状子图一一对应并且相同. 使节点数减少或保持不变,而节点数保持不变的重 在从形状图的等价规则构造重写系统时,可以 写情况受上面两条的限定,因此归约一定会终止, 忽略如图4那样仅替换浓缩节点的e和a的那些等 R的合流性可以参照项重写系统合流性的证明 价规则,因为定义1已把替换前后的浓缩节点定义 方法来证明,首先考虑临界对,例如,由图9的等价 为相同 规则(1)和(2)得到两条重写规则R1和R2,R1和R2 在完备化过程中,文献[10]中2.3节的(循环) 的左部(对应图9等价规则(1)和(2)的右部)经两种 单链表、(循环)双向链表和二叉树的等价规则按照 节点数减少的方向定为重写规则,例如图9的等价 方式合一,得到2个临界对,分别是图10的(1)和 规则(1)和(2)定向为从右向左的重写规则.规则(1) (2)与图10的(3)和(4),它们分别都能化简到相同 和(2)其实是同一条规则,只要把其中一条规则中边 的窗口.其余的临界对也都是由于规则的窗口中有 上的标记r和1对调一下就可看出,这里写成两条 (循环)单链表、(循环)双向链表或二叉树的浓缩节 是为了便于下面理解和讨论临界对.对那些两边节 点而产生的,例如对应图3(1)和(2)的相应重写规 则也会产生2个临界对.很容易检查它们都可归约 到同样的窗口,因而证明R是局部合流的.再根据R 的局部合流性和终止性可以证明R是合流的 (e 1》 (1) (2) (2 eu,a e-1,a es ag a→(e>=1)/Aa,=(e>=1) a,→fe>=1)/Aa,→(e>=1) (3) (4) 图10临界对的两个例子 基于形状图等价重写系统以及图4这样的规 则,参照代数项上的证明方法,不难证明下面的 定理 cJlist,e.a 定理.形状图G1和G2等价,即G1台G2,当且 仅当它们化简后的最简形状图G和G相同。 3.2G.1V…VG1.m台G21V…VG2.m的判定方法 抽象地说,判定G11V…VGm台G2.1V…V G2.m可以先用3.1节的等价重写系统把两边所有的 (5) 形状图分别化简,然后比较两边的各个最简形状图 图9等价规则的一些例子 是否都能在对方找到相同的形状图.但是3.1节的
节点在此都被视为带犿与犿>=0的浓缩节点.下 面讨论判定方法时也作如此假设. 定义2.形状子图犌1和犌2若满足下面两个条 件,则称犌1和犌2相同. (1)犌1和犌2的节点一一对应. (2)犌1和犌2的对应节点都是相同节点,并且若 它们有出边,则标记相同的出边所指向的节点是对 应节点.定义3.形状图犌1和犌2若满足下面的条件, 则称犌1和犌2相同. 犌1和犌2的形状子图一一对应并且相同. 在从形状图的等价规则构造重写系统时,可以 忽略如图4那样仅替换浓缩节点的e和a的那些等 价规则,因为定义1已把替换前后的浓缩节点定义 为相同.在完备化过程中,文献[10]中2.3节的(循环) 单链表、(循环)双向链表和二叉树的等价规则按照 节点数减少的方向定为重写规则,例如图9的等价 规则(1)和(2)定向为从右向左的重写规则.规则(1) 和(2)其实是同一条规则,只要把其中一条规则中边 上的标记r和l对调一下就可看出,这里写成两条 图9等价规则的一些例子 是为了便于下面理解和讨论临界对.对那些两边节 点数相等的各种等价规则,可按下面的方式之一 定向: (1)对于1个结构节点和e等于1的浓缩节点 之间的等价规则,定向为向浓缩节点的重写,例如 图9(3)定向为从左向右.按这个方向定向是便于若 干个相邻的结构节点归约成浓缩节点. (2)对于出自链表定义的等价规则,定向为向 谓词节点的重写,例如图9的规则(4)和(5)定向为 从右向左.形状图的归约一定会终止,因为每次归约都会 使节点数减少或保持不变,而节点数保持不变的重 写情况受上面两条的限定,因此归约一定会终止. $的合流性可以参照项重写系统合流性的证明 方法来证明.首先考虑临界对,例如,由图9的等价 规则(1)和(2)得到两条重写规则犚1和犚2.犚1和犚2 的左部(对应图9等价规则(1)和(2)的右部)经两种 方式合一,得到2个临界对,分别是图10的(1)和 (2)与图10的(3)和(4),它们分别都能化简到相同 的窗口.其余的临界对也都是由于规则的窗口中有 (循环)单链表、(循环)双向链表或二叉树的浓缩节 点而产生的,例如对应图3(1)和(2)的相应重写规 则也会产生2个临界对.很容易检查它们都可归约 到同样的窗口,因而证明$是局部合流的.再根据$ 的局部合流性和终止性可以证明$是合流的. 图10临界对的两个例子 基于形状图等价重写系统以及图4这样的规 则,参照代数项上的证明方法,不难证明下面的 定理.定理.形状图犌1和犌2等价,即犌1犌2,当且 仅当它们化简后的最简形状图犌′1和犌′2相同. 32犌1,1∨…∨犌1,犿犌2,1∨…∨犌2,狀的判定方法 抽象地说,判定犌1,1∨…∨犌1,犿犌2,1∨…∨ 犌2,狀可以先用3.1节的等价重写系统把两边所有的 形状图分别化简,然后比较两边的各个最简形状图 是否都能在对方找到相同的形状图.但是3.1节的 12期 张昱等:形状图理论的定理证明 2467

2468 计算 机 学报 2016年 等价重写系统并未考虑个数不同的形状图之间的等 3.3 G.1V…VG.m→G2.1V…VG2.n的判定方法 价性,为此需要利用文献[10]中2.3节里的W台 该判定方法用于程序分析和验证过程中对形状 W:VW2等价规则(如图11)展开形状图,以期建立 图蕴涵关系的判定,例如第4节的循环不变形状图 个数不同的形状图之间的等价性.结合应用场合的 和递归函数前后形状图的推断算法需要用到该方 特点,本文讨论的等价式中各形状图的声明变量集 法.先定义节点相容和形状图相容。 都相同,等价式的判定方法如下: 定义4.节点n1和2若满足下面的条件,则 1相容于2(与定义1的区别仅在条件(2)). (1)1和n2是同类节点.并且若都是声明节点、 结构节点或浓缩节点,则有同样的出边及其标记:若 都是谓词节点,则谓词名相同。 (2)若1和2是同类浓缩节点或谓词节点,且 图11从二叉树定义得到的等价规则 分别带e1与a1和e2与a2,则必须满足(e1==e2 (1)若G.1和G2.1的声明变量集不同则该等价 a1)→a2. 式不成立,否则继续下面步骤. 定义5.形状子图G1和G2若满足下面3个条 (2)将上式中所有的形状图,用3.1节介绍的 件,则称G1相容于G2: 形状图重写系统把它们归约到最简形状图.仍用原 (1)G的节点集N到G2的节点集N2有一对一 来的符号G1.(1≤i≤m)或G2,(1≤j≤n)代表各形 的函数f,使得N2一f(N1)若非空,则其中只有浓 状图的最简形状图. 缩节点并且每个浓缩节点的(e==0)八a可满足, (3)若某个G1.:(1≤i≤m)的某条尽可能长的且 即这些浓缩节点可以有e等于0的情况, 不经过浓缩节点的访问路径是某个G2.,(1≤j≤n) (2)对任何n∈N1,n相容于f(n). 的某条不经过浓缩节点的访问路径的真前缀,并且 (3)对任何n∈N1,若n和f(n)的某标记相 若G1.:中的这条访问路径指向的节点可以用W台 同的出边分别指向节点1和2,则2经过m个 W1VW,的等价规则展开,则将其展开.反之亦然.直 (m≥0)属于N2一f(N1)的浓缩节点后所到达的2 到不存在这样的路径或者虽存在但不能展开为止. 和1满足f(11)=n2, 为防止滥用W台W,VWz这类等价规则,需要 对于图12的G1和G2,G1的那个浓缩节点经f 从访问路径的比较上加以限制.例如,若G1:中有不 函数映射到G2最右边的那个浓缩节点.因为G2左 能再延长的二叉树访问路径p→1,G2,中有访问路 边两个浓缩节点的和k都可以等于0,所以G1相 径p→r,且在G:中p→1指向谓词节点,则可以 容于G2. 根据图11的二叉树等价规则将G1:展开,其中等价 规则中的s是占位符,可以通配访问路径p→1中的 1.该规则由图2的二叉树定义得到. 文献[10]中2.3节里的所有的W台W,VW2都 像图11这样,右边W1或W2中指向谓词节点或浓缩 节点的访问路径比W的多一个结构体的指针域,因 此不会出现等价式左右两边的形状图不断交替展开 nt 而不终止的情况 经过这样的展开,原等价式变换成G.:V…V m>=0Am=0Mk<8 G Gim台G2.,V…VG2.. (4)对每个G1:(1≤i≤m'),若存在某个G2 图12帮助理解定义5的两个形状图 (1≤≤n'),使得G:和G2相同,并且反之亦然,则 定义6.形状图G1和G2若满足下面的条件, G.1V…VG1m台G2.1V…VG2m,否则该式不成立. 则称G相容于G2. 显然,若上述方法中涉及的由整型线性表达式 G,和G2的形状子图一一对应并且G的每个形 之间的关系式所构成的断言都可判定,则G.1V…V 状子图相容于G2中对应的形状子图. G1.m台G2.1V…VG2n可判定. 在证明形状图之间的蕴涵时,需要考虑在用等
等价重写系统并未考虑个数不同的形状图之间的等 价性,为此需要利用文献[10]中2.3节里的犠 犠1∨犠2等价规则(如图11)展开形状图,以期建立 个数不同的形状图之间的等价性.结合应用场合的 特点,本文讨论的等价式中各形状图的声明变量集 都相同,等价式的判定方法如下: 图11从二叉树定义得到的等价规则 (1)若犌1,1和犌2,1的声明变量集不同则该等价 式不成立.否则继续下面步骤. (2)将上式中所有的形状图,用3.1节介绍的 形状图重写系统把它们归约到最简形状图.仍用原 来的符号犌1,犻(1犻犿)或犌2,犼(1犼狀)代表各形 状图的最简形状图. (3)若某个犌1,犻(1犻犿)的某条尽可能长的且 不经过浓缩节点的访问路径是某个犌2,犼(1犼狀) 的某条不经过浓缩节点的访问路径的真前缀,并且 若犌1,犻中的这条访问路径指向的节点可以用犠 犠1∨犠2的等价规则展开,则将其展开.反之亦然.直 到不存在这样的路径或者虽存在但不能展开为止. 为防止滥用犠犠1∨犠2这类等价规则,需要 从访问路径的比较上加以限制.例如,若犌1,犻中有不 能再延长的二叉树访问路径狆→l,犌2,犼中有访问路 径狆→l→r,且在犌1,犻中狆→l指向谓词节点,则可以 根据图11的二叉树等价规则将犌1,犻展开,其中等价 规则中的s是占位符,可以通配访问路径狆→l中的 l.该规则由图2的二叉树定义得到. 文献[10]中2.3节里的所有的犠犠1∨犠2都 像图11这样,右边犠1或犠2中指向谓词节点或浓缩 节点的访问路径比犠的多一个结构体的指针域,因 此不会出现等价式左右两边的形状图不断交替展开 而不终止的情况. 经过这样的展开,原等价式变换成犌′1,1∨…∨ 犌′1,犿′犌′2,1∨…∨犌′2,狀′. (4)对每个犌′1,犻(1犻犿′),若存在某个犌′2,犼 (1犼狀′),使得犌′1,犻和犌′2,犼相同,并且反之亦然,则 犌1,1∨…∨犌1,犿犌2,1∨…∨犌2,狀,否则该式不成立. 显然,若上述方法中涉及的由整型线性表达式 之间的关系式所构成的断言都可判定,则犌1,1∨…∨ 犌1,犿犌2,1∨…∨犌2,狀可判定. 33犌1,1∨…∨犌1,犿犌2,1∨…∨犌2,狀的判定方法 该判定方法用于程序分析和验证过程中对形状 图蕴涵关系的判定,例如第4节的循环不变形状图 和递归函数前后形状图的推断算法需要用到该方 法.先定义节点相容和形状图相容. 定义4.节点狀1和狀2若满足下面的条件,则 狀1相容于狀2(与定义1的区别仅在条件(2)). (1)狀1和狀2是同类节点.并且若都是声明节点、 结构节点或浓缩节点,则有同样的出边及其标记;若 都是谓词节点,则谓词名相同. (2)若狀1和狀2是同类浓缩节点或谓词节点,且 分别带e1与a1和e2与a2,则必须满足(e1==e2∧ a1)a2.定义5.形状子图犌1和犌2若满足下面3个条 件,则称犌1相容于犌2. (1)犌1的节点集犖1到犌2的节点集犖2有一对一 的函数犳,使得犖2-犳(犖1)若非空,则其中只有浓 缩节点并且每个浓缩节点的(e==0)∧a可满足, 即这些浓缩节点可以有e等于0的情况. (2)对任何狀∈犖1,狀相容于犳(狀). (3)对任何狀∈犖1,若狀和犳(狀)的某标记相 同的出边分别指向节点狀1和狀2,则狀2经过犿个 (犿0)属于犖2-犳(犖1)的浓缩节点后所到达的狀′2 和狀1满足犳(狀1)=狀′2. 对于图12的犌1和犌2,犌1的那个浓缩节点经犳 函数映射到犌2最右边的那个浓缩节点.因为犌2左 边两个浓缩节点的犿和犽都可以等于0,所以犌1相 容于犌2. 图12帮助理解定义5的两个形状图 定义6.形状图犌1和犌2若满足下面的条件, 则称犌1相容于犌2. 犌1和犌2的形状子图一一对应并且犌1的每个形 状子图相容于犌2中对应的形状子图. 在证明形状图之间的蕴涵时,需要考虑在用等 2468 计 算 机 学 报 2016年

12期 张昱等:形状图理论的定理证明 2469 价重写系统化简形状图后,适当地使用形状图的蕴 使用的双向链表倒置算法。 涵规则.所使用的蕴涵规则是2.2节中第(1)类蕴涵 对于这类循环,在循环体的每条执行路径上,声 规则,即由W台W,VW2得到的W→W和W2→W: 明指针在形状图上的移动引起的形状图变化主要体 而对于第(2)和(3)类蕴涵规则,由于它们都是针对 现在浓缩节点所代表的节点个数的变化上 浓缩节点的e和a的规则,其效果已体现在节点相 4.1循环不变形状图推断算法的框架 容的定义中,因而不必作为重写规则 根据基于抽象解释的循环不变式推断框架[四, G1.1V…VG1.m→G2.1V…VG2n的判定方法可 循环不变形状图的推断算法框架如图13.为表达简 通过略微修改3.2节的等价式判断方法中的(3)和 单起见,本节用字母9表示可以出现形状图析取的 (4)两点即可得到: 形状图. (3)若某个G2(1≤≤n)的某条尽可能长的且 不经过浓缩节点的访问路径是某个G1.:(1≤i≤m) 对于循环while(B)S (1)计算循环前条件Go=Gm.i=0. 的某条不经过浓缩节点的访问路径或其真前缀,但 (2)根据形状图逻辑的规则计算G+1,使得 不是指向同类节点,则尝试使用上面提到的蕴涵规 (G:A B)SIG+). (3)应用抽象规则计算G:+1,使得G+1→G:+1. 则对G:进行重写. (4)若G+1→SoV…VG:,则GoV…VG:是循环不变形状 例如,若图11规则右部两个窗口之一和左部窗 图,否则,i=十1,转(2). 口分别出现在G1:和G2中的上述位置,则使用相应 图13循环不变形状图推断的算法框架 蕴涵规则重写G1,把窗口中内容归约成谓词节点. (4)对每个G1(1≤i≤m),若存在某个G2 下面对图13的算法框架做一些解释: (1≤j≤n),使得G1:相容于G2,则GV…VG1.m→ (1)算法第(2)步根据形状图逻辑的规则计算 G2.V…VG2m,否则该蕴涵式不成立 G+1,G:∧B代表形状图g:和符号断言B的合取, 若碰到引起内存泄漏的操作、悬空指针或null指 4 循环不变形状图和递归函数前后 针脱引用(dereference)操作,则无规则可用,报告 形状图的推断 错误 (2)算法第(3)步的抽象是指:对形状图上随循 本节应用第3节的形状图理论判定方法来推断 环迭代次数变化而变化的浓缩节点(指其代表的结 循环不变形状图.该推断方法的一个变种可用来推 构节点数随迭代次数变化而变化),把其代表结构节 断递归函数的前后形状图. 点数的表达式换成能概括多次(甚至全部)迭代情况 形状图是指针有效性和指针相等性断言的集合 的表达式.应用的抽象规则是采用文献[10]中第 的图形表示,循环不变形状图就是循环不变式中有 2.3节的蕴涵规则, 关指针断言的那部分不变式,函数前后形状图就是 (3)算法第(4)步G+1→gV…V9:的证明是采 函数前后条件中有关指针的那部分断言. 用3.3节的判定方法, 对易变数据结构的处理,循环语句通常完成下 以2.3节的那段单链表代码(假定至少有一个 面功能之一: 表元)的循环不变形状图(图8(1))的推断为例.各 (1)寻找数据结构中的操作位置或依次对各节 程序点的形状图见图14,图中j是形状分析系统引 点上数据进行操作,这时,除了某些声明指针的指向 入的虚拟变量.第1次迭代后G1→G不成立,但第2 在节点间移动外,形状图没有其他变化。 次迭代后能证明G2→G。VG1,因此G。VG1是循环 (2)循环体的每次迭代都在对数据结构进行节 不变形状图.由于G→G,因此GVG1可简化为 点插入或删除.循环体执行过程中虽然破坏了数据 G1.由于没有程序变量可以替代G1中的虚拟变量j, 结构的形状,但每次到达循环体结束点时,形状得到 则略去j,得到结果就是图8(1). 恢复,仅节点个数发生变化 4.2算法终止的讨论 (3)循环体的每次迭代都在对数据结构某些节 图13算法终止取决于下面3点: 点的边的指向进行调整,并且有可能出现这样的情 (1)算法第(3)步的抽象能够成功 况:每次迭代结束时形状并未得到恢复,但在整个循 (2)算法第(4)步的蕴涵式的证明因得到结果 环执行结束时形状得到恢复,例如文献[10]中例2 而终止或因形状检查发现错误而终止
价重写系统化简形状图后,适当地使用形状图的蕴 涵规则.所使用的蕴涵规则是2.2节中第(1)类蕴涵 规则,即由犠犠1∨犠2得到的犠1犠和犠2犠; 而对于第(2)和(3)类蕴涵规则,由于它们都是针对 浓缩节点的e和a的规则,其效果已体现在节点相 容的定义中,因而不必作为重写规则. 犌1,1∨…∨犌1,犿犌2,1∨…∨犌2,狀的判定方法可 通过略微修改3.2节的等价式判断方法中的(3)和 (4)两点即可得到: (3)若某个犌2,犼(1犼狀)的某条尽可能长的且 不经过浓缩节点的访问路径是某个犌1,犻(1犻犿) 的某条不经过浓缩节点的访问路径或其真前缀,但 不是指向同类节点,则尝试使用上面提到的蕴涵规 则对犌1,犻进行重写. 例如,若图11规则右部两个窗口之一和左部窗 口分别出现在犌1,犻和犌2,犼中的上述位置,则使用相应 蕴涵规则重写犌1,犻,把窗口中内容归约成谓词节点. (4)对每个犌1,犻(1犻犿),若存在某个犌2,犼 (1犼狀),使得犌1,犻相容于犌2,犼,则犌1,1∨…∨犌1,犿 犌2,1∨…∨犌2,狀,否则该蕴涵式不成立. 4循环不变形状图和递归函数前后 形状图的推断 本节应用第3节的形状图理论判定方法来推断 循环不变形状图.该推断方法的一个变种可用来推 断递归函数的前后形状图. 形状图是指针有效性和指针相等性断言的集合 的图形表示,循环不变形状图就是循环不变式中有 关指针断言的那部分不变式,函数前后形状图就是 函数前后条件中有关指针的那部分断言. 对易变数据结构的处理,循环语句通常完成下 面功能之一: (1)寻找数据结构中的操作位置或依次对各节 点上数据进行操作.这时,除了某些声明指针的指向 在节点间移动外,形状图没有其他变化. (2)循环体的每次迭代都在对数据结构进行节 点插入或删除.循环体执行过程中虽然破坏了数据 结构的形状,但每次到达循环体结束点时,形状得到 恢复,仅节点个数发生变化. (3)循环体的每次迭代都在对数据结构某些节 点的边的指向进行调整,并且有可能出现这样的情 况:每次迭代结束时形状并未得到恢复,但在整个循 环执行结束时形状得到恢复.例如文献[10]中例2 使用的双向链表倒置算法. 对于这类循环,在循环体的每条执行路径上,声 明指针在形状图上的移动引起的形状图变化主要体 现在浓缩节点所代表的节点个数的变化上. 41循环不变形状图推断算法的框架 根据基于抽象解释的循环不变式推断框架[11], 循环不变形状图的推断算法框架如图13.为表达简 单起见,本节用字母%表示可以出现形状图析取的 形状图. 对于循环while(犅)犛 (1)计算循环前条件%0=%狆狉犲.犻=0. (2)根据形状图逻辑的规则计算%′犻+1,使得 {%犻∧犅}犛{%′犻+1}. (3)应用抽象规则计算%犻+1,使得%′犻+1%犻+1. (4)若%犻+1%0∨…∨%犻,则%0∨…∨%犻是循环不变形状 图;否则,犻=犻+1,转(2). 图13循环不变形状图推断的算法框架 下面对图13的算法框架做一些解释: (1)算法第(2)步根据形状图逻辑的规则计算 %′犻+1,%犻∧犅代表形状图%犻和符号断言犅的合取[11]. 若碰到引起内存泄漏的操作、悬空指针或null指 针脱引用(dereference)操作,则无规则可用,报告 错误.(2)算法第(3)步的抽象是指:对形状图上随循 环迭代次数变化而变化的浓缩节点(指其代表的结 构节点数随迭代次数变化而变化),把其代表结构节 点数的表达式换成能概括多次(甚至全部)迭代情况 的表达式.应用的抽象规则是采用文献[10]中第 2.3节的蕴涵规则. (3)算法第(4)步%犻+1%0∨…∨%犻的证明是采 用3.3节的判定方法. 以2.3节的那段单链表代码(假定至少有一个 表元)的循环不变形状图(图8(1))的推断为例.各 程序点的形状图见图14,图中犼是形状分析系统引 入的虚拟变量.第1次迭代后犌1犌0不成立,但第2 次迭代后能证明犌2犌0∨犌1,因此犌0∨犌1是循环 不变形状图.由于犌0犌1,因此犌0∨犌1可简化为 犌1.由于没有程序变量可以替代犌1中的虚拟变量犼, 则略去犼,得到结果就是图8(1). 42算法终止的讨论 图13算法终止取决于下面3点: (1)算法第(3)步的抽象能够成功. (2)算法第(4)步的蕴涵式的证明因得到结果 而终止或因形状检查发现错误而终止. 12期 张昱等:形状图理论的定理证明 2469