一个程序验证器的设计和实现 An Automatic Program Verifier for PointerC.pdf_大学文库

计算机研究与发展 ISSN1000-1239/CN11-1777/TP Journal of Computer Research and Development 50(5):1044-1054,2013 一个程序验证器的设计和实现张志天李兆鹏陈意云刘刚 (中国科学技术大学计算机科学技术学院合肥230026) (中国科学技术大学苏州研究院软件安全实验室江苏苏州215123) (zpli@ustc.edu.cn) An Automatic Program Verifier for PointerC:Design and Implementation Zhang Zhitian,Li Zhaopeng,Chen Yiyun,and Liu Gang (School of Computer Science and Technology.University of Science and Technology of China.Hefei 230026) (So ftware Security Laboratory.Suzhou Institute for Advanced Study.University of Science and Technology of China, Suzhou.Jiangsu 215123) Abstract Formal verification is a major method to improve the dependability of software.One of the hot research areas is automatic program verification based on logical inference.So far there is no product which can be used directly in the industries,and the root of this problem lies in the slow development and difficulties of automated theorem proving.Our approach is based on the observation that program analysis methods can be used in collecting global information to support program verification.We build shape graphs at each program point in the program analysis phase.A method is proposed,which uses regular Hoare logic rules to reason about assignment not dealing with pointers in a C-like programming language.Such rules will be applied after aliasing is eliminated using the information of shape graphs.The soundness of the logic system has been proved.Furthermore,an approach is presented to verify data constraints on mutable data structures without using user-defined predicates.A prototype of our program verifier has been implemented for the PointerC programming language.We have used it in the verification of programs manipulating recursive data structures,such as lists and trees,and programs dealing with one-dimension arrays. Key words program verification;Hoare logic;shape graph logic;program analysis;separation logic 摘要形式验证是提高软件可信程度的重要方法，基于逻辑推理对程序性质进行严格的自动证明是当前的研究热点，但尚无可供工业界使用的产品，其根源在于自动定理证明方面的困难.介绍在通过程序分析建立起各程序点的形状图的基础上，如何利用形状图提供的信息来支持程序验证的方法，提出一种利用形状图信息来消除访问路径别名，使得指针程序中非指针部分的性质仍然可以用Hore逻辑来进行验证的方法，并证明了该方法的可靠性.还提出一种在不使用自定义谓词的情况下，易变数据结构上数据性质的描述和验证方法，另外，介绍所设计并实现的基于上述方法的PointerC语言的程序验证器的原型.它不仅能自动验证操作易变数据结构程序的性质，也能自动验证使用一雏数组的程序的性质. 关键词程序验证；Hoare逻辑；形状图逻辑；程序分析；分离逻辑中图法分类号TP301 收稿日期：2010-11-29：修回日期：2012-12-10 基金项目：国家自然科学基金项日(61170018,61003043) 通信作者：李兆鹏(zpli@ustc.edu.cm)

张志天等：一个程序验证器的设计和实现 1045 随着国家、社会和日常生活对软件系统的依赖在下面的三元式中：程度日益增长，复杂软件系统的正确、安全（包括可 {Q}*p=5{p==qΛ*p+*q==10}, 靠安全性(safety)和保密安全性(security))和可靠访问路径￥p和*g互为别名.若按Hoare逻辑的赋等对安全攸关的基础设施和应用是至关重要的，安值公理，最弱前条件Q是p==q∧*q==5,而正确全攸关软件的高可信成了保障国家安全、保持经济的最弱前条件是p==q. 可持续发展和维护社会稳定的必要条件。对于访问路径的别名，一种针对性的解决办法形式验证是提高软件可信程度的重要方法，粗是引入存储模型，把存储器M看成地址到被存储值略地说，软件的形式验证有两种途径.第1种途径是的映射，并且有下面的存储器公理，其中E和E 模型检测]，它通过遍历系统所有状态空间，能够对是地址表达式，E2是值表达式：有穷状态系统进行自动验证，并自动构造不满足验 select(update(M,E1,E2),Es)=E2,if E== 证性质的反例.这种方法在工业界比较流行，其优点 E3; 是需要最小的用户交互，并可用于大规模复杂系统， select(update (M,E1,E2),Es)=select (M, 近年来广泛用于清扫现有代码的错误上.第2种途 Es),ifE1！=E 径是逻辑推理，它采用程序逻辑，比较有影响的是然后，将Hoare逻辑的赋值公理修改为 Hoare逻辑)，对程序的性质进行严格地推理，并且 (Q[update(u,E1,E2)/u]*E1=E2 (Q), 在推理过程中通常需要使用像Isabellets]或Cog) 其中，牡是存储器当前状态.利用该赋值公理和存储这样的定理证明器.在这种途径中，大部分研究围绕器公理，对先前的那个例子进行演算，可以得到最弱采用某种演算来产生验证条件，然后用某个定理证前条件p==q.这种办法的缺点是需要引入语义模明器来证明验证条件，如Ynot),Spec#[)和ESC 型 Java[们.有些研究依靠符号计算及其过程中的定理另一种解决办法是采用分离逻辑门.分离逻辑证明来避免验证条件生成步骤，如Smalllfoots]和通过把动态分配的各堆块的断言分离地表示，使得 jStar).还有的研究采用经严格证明的变换，从抽象别名仅可能出现在同一个堆块的断言中.再通过对规范逐步求精得到具体程序，如Perfect Developer. 赋值语句的推理规则的特别设计，使得必须先消除虽然这些工具已在实验室研发出来，但是尚无可供堆断言中出现的别名，然后才可以对修改该堆块单工业界使用的产品问世.究其原因，根源在于自动定元的赋值语句进行推理.使用分离逻辑的一个问题理证明方面的困难.因为不管是访问路径的别名判是，通常的自动定理证明器都不能证明带分离合取断、循环不变式的推断、断言语言的表达能力和领域连接词(*，separating conjunction)的验证条件，必专用逻辑的设计等，最终都受到自动定理证明的能须为分离逻辑设计专用的自动定理证明工具.而使力的影响. 用这种自动定理器，规范的表达性受限于分离逻辑在研究自动定理证明技术的同时，也应该考虑的一个可判定片段(fragment)a 怎样降低对自动定理证明器的能力的要求.例如，设在对操作易变数据结构的程序进行验证时，在计新的编程语言机制来提高合法程序的门槛，以排各程序点形状图的支持下，本文方法仍然基于普通除部分有逻辑错误的程序.还有采用其他程序分析的Hoare逻辑，既不需要从语义角度对它扩展，也方法来收集程序信息，用这些信息来支持程序验证· 不需要引入新的逻辑连接词，既方便了程序员也减这些都有可能减轻程序验证的负担，本文介绍在通轻了自动定理证明器的负担. 过程序分析建立起各程序点形状图(shape graph) 其次，本文提出一种在不使用自定义谓词的情的基础上，如何利用形状图提供的信息来支持程序况下，易变数据结构上数据性质的描述和验证方法. 验证的方法，介绍基于该方法开发的一个程序验证主要是指断言中允许使用带上角标的访问路径（即器原型。 p(->ext)代表p->next->…->next,其中本文的主要贡献是提出一种利用形状图信息来 ->next重复i次)，以便用带全称量词的断言描述消除访问路径别名，使得指针程序仍然可以用Hoare 链表的有序性等性质.在产生验证条件时，通过引入逻辑来进行验证的方法，并证明了该方法的可靠性. 辅助函数来把带上角标的访问路径变换成可满足性 Hoare逻辑的一个重要限制是程序中不同的名模理论(satisfiability modulo theories)求解器Z3ls町字代表不同的程序对象，即不允许出现别名.例如，能接受的形式」

1046 计算机研究与发展2013,50(5) 最后，本文介绍我们所设计并实现的基于上述是按形状分析的需求所作的语言扩展，所允许的形方法的PointerC语言的程序验证器的原型.它不仅状有单链表、循环单链表、双向链表、循环双向链表能自动验证操作易变数据结构程序的性质，也能自和二叉树等.在图1的文法中，有关表达式的部分产动验证使用一维数组程序的性质生式被略去，assertion的语法在用到时再解释。在PointerC中，指针类型的变量只能用于赋 1 PointerC语言和形状图逻辑简介值、相等比较、存取指向对象等运算以及作为函数的参数：指针算术和取地址运算(&)被禁止，并且没有本节介绍验证器面向的编程语言PointerC和指向指针类型的指针类型.malloc和free被看成是验证器所依赖的形状图逻辑(shape graph logic)). PointerC预定义的函数，并且满足安全程序的最基 1.1 PointerC语言本要求，例如malloc任何一次调用都能成功并且所 PointerC是一种强调指针类型并增加形状声明分配空间同尚未释放空间无任何重叠。的类C小语言，语法的主要产生式如图1所示.在 1.2形状图和形状图逻辑结构体声明中，通过指针域指向形状的声明来确定程序验证之前需要先基于形状图逻辑对程序进这种结构体用来构造什么形状的数据结构.这同时行形状分析为每个程序点构建形状图，这些形状图也限定了该结构体类型的指针所能指向的形状.这构成了程序验证所需要的指针信息.在此通过举例 program::=struct_def_list var_dec_list fun_def_list 来介绍形状图，形状图的严格定义请见文献[14幻. struct_def_list::=struct_def_list struct_defle 图2(a)是用形状图给出的单链表的归纳定义 struct_def::=typedef struct id field_dec_list)type_name; list(s).圆节点称为声明节点，代表指针型的声明变 var_dec_list::=var_dec_list var_decle var_dec::=type id_list: 量，唯一的出边上的标记是该变量的名字.框中没有 field_dec_list::=field_dec_list field_declfield_dec 标记的实线矩形称为结构节点，代表用malloc生成 field_dec::=field_type id; 的结构体变量，其出边代表它的指针域，边上的标记 id_list::=id_list,idid 是域名.框中有标记P的实线矩形称为谓词节点， fun_def_list::=fun_def_list fun_def\fun_def fun_def::=type id(param_list)bodyltype id()body 框的下方是该谓词的名字，谓词节点没有出边.框中 Param_list::=param_type id param_list.param_type id 有标记W的虚线矩形称为NULL节点，表示指向 body::=(entry_assertion var_dec_list stmt_list exit_assertion 它的边代表NULL指针.类似地，有标记的D虚线 type::=simple_typelelement_type [number]type_nameIvoid type_name::=id 矩形称为悬空节点，表示指向它的边代表悬空指针. element_type::=simple_type 图2(a)的谓词定义list(s)表示单链表分成空表(s field_type::=simple_typeltype_name":shape 是NULL指针)和非空(s指向一个结构节点，该节 param_type::=simple_typeltype_name" simple_type::=boollint GG9G巴 shape:=LISTIDLISTIC_LISTIC_DLISTITREEI.. list list entry_assertion::=assertion assertion:e (a)Definition of list (s) exit_assertion::=assertion assertion:e stmt_list:=stmt_list stmtlstmt stmt::=lval=exp:lval=malloc(type_name):if(exp)block lif(exp)block else block while(exp)loop_invariant block list,n.a n,a Ilval=id(exp_list):lid(exp_list):lal=id():lid(): (b)Definition of list (s,n,a) return:Ireturn exp:free(lval): block::=stmtlstmt_list) loop_invariant::=loop_invariant assertion:le exp::=numberl lval|NULLItruelfalse c dlist.n,a l-expl!explexp op expl(exp) (a→(n==0) (a→(n≥1) lval::=id\lval->id id Lexp] (c)Definition of c dlist (s,n,a) Fig.I Representative syntax of PointerC language. Fig.2 Three definitions of linked list. 图1 PointerC语言的语法（部分）图2链表的几种定义

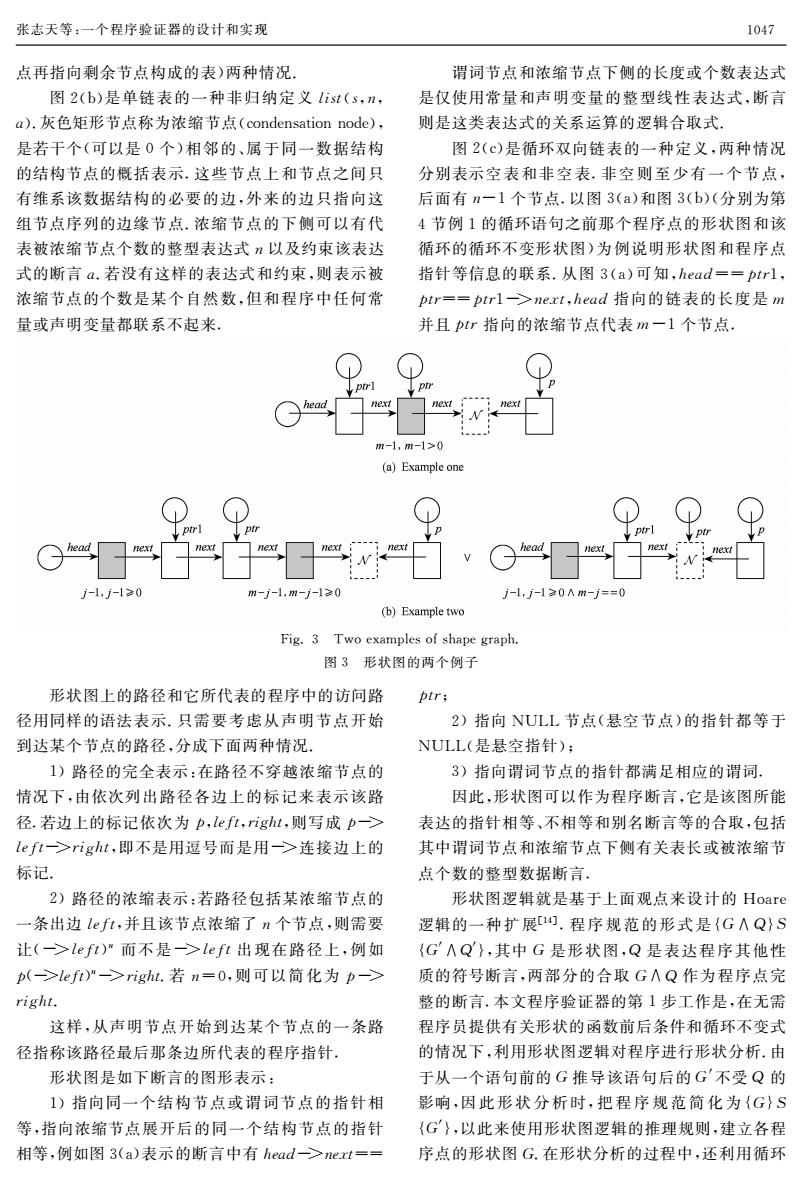
张志天等：一个程序验证器的设计和实现 1047 点再指向剩余节点构成的表)两种情况谓词节点和浓缩节点下侧的长度或个数表达式图2(b)是单链表的一种非归纳定义list(s,n, 是仅使用常量和声明变量的整型线性表达式，断言 a).灰色矩形节点称为浓缩节点(condensation node), 则是这类表达式的关系运算的逻辑合取式，是若干个（可以是0个）相邻的、属于同一数据结构图2(c)是循环双向链表的一种定义，两种情况的结构节点的概括表示.这些节点上和节点之间只分别表示空表和非空表.非空则至少有一个节点，有维系该数据结构的必要的边，外来的边只指向这后面有n一1个节点.以图3(a)和图3(b)(分别为第组节点序列的边缘节点，浓缩节点的下侧可以有代 4节例1的循环语句之前那个程序点的形状图和该表被浓缩节点个数的整型表达式n以及约束该表达循环的循环不变形状图)为例说明形状图和程序点式的断言a.若没有这样的表达式和约束，则表示被指针等信息的联系.从图3(a)可知，head==ptrl, 浓缩节点的个数是某个自然数，但和程序中任何常 ptr==ptrl>next,head指向的链表的长度是m 量或声明变量都联系不起来。并且tr指向的浓缩节点代表m一1个节点 m-1,m-1>0 (a)Example one □w G next j-1,i-10 m-j-1,m-j-10 j-1,j-10Am-j==0 (b)Example two Fig.3 Two examples of shape graph. 图3形状图的两个例子形状图上的路径和它所代表的程序中的访问路 ptr: 径用同样的语法表示.只需要考虑从声明节点开始 2)指向NULL节点（悬空节点）的指针都等于到达某个节点的路径，分成下面两种情况 NULL(是悬空指针)： 1)路径的完全表示：在路径不穿越浓缩节点的 3)指向谓词节点的指针都满足相应的谓词。情况下，由依次列出路径各边上的标记来表示该路因此，形状图可以作为程序断言，它是该图所能径.若边上的标记依次为p,left,right,则写成p-> 表达的指针相等、不相等和别名断言等的合取，包括 left>right,即不是用逗号而是用->连接边上的其中谓词节点和浓缩节点下侧有关表长或被浓缩节标记点个数的整型数据断言， 2)路径的浓缩表示：若路径包括某浓缩节点的形状图逻辑就是基于上面观点来设计的Hoare 一条出边left,并且该节点浓缩了n个节点，则需要逻辑的一种扩展1).程序规范的形式是{G∧Q}S 让(->left)而不是->left出现在路径上，例如 {G'八Q〉，其中G是形状图，Q是表达程序其他性 (>left)"->right..若n=0,则可以简化为p-> 质的符号断言，两部分的合取G八Q作为程序点完 right. 整的断言.本文程序验证器的第1步工作是，在无需这样，从声明节点开始到达某个节点的一条路程序员提供有关形状的函数前后条件和循环不变式径指称该路径最后那条边所代表的程序指针」的情况下，利用形状图逻辑对程序进行形状分析.由形状图是如下断言的图形表示：于从一个语句前的G推导该语句后的G'不受Q的 1)指向同一个结构节点或谓词节点的指针相影响，因此形状分析时，把程序规范简化为{G}S 等，指向浓缩节点展开后的同一个结构节点的指针 {G〉，以此来使用形状图逻辑的推理规则，建立各程相等，例如图3(a)表示的断言中有head->ne.xt== 序点的形状图G.在形状分析的过程中，还利用循环

1048 计算机研究与发展2013,50(5) 不变式推断算法得出各循环的循环不变形状图) 影响符号断言：符号断言中若有以“或u为前缀的在完成形状分析后，程序验证器进行程序其他访问路径，则要用和u相等但不是别名的'来代换性质Q的验证.在{G∧Q}S{G'∧Q'}中，若S不是 u.另一个影响符号断言的场合是，在free语句之后指针操作语句，则G和G一样，但Q可能不同于Q. 应该删除涉及被释放节点上数据的原子断言. 若S是指针操作语句（指针赋值、分配空间和释放 G中也会有符号断言，附加在浓缩节点上，用来空间等)，则除了G'和G可能不同外，Q'和Q可能限制它代表结构节点的个数.G的符号断言和Q的也有一些细微的区别，这是本文下面关注的部分. 符号断言不会有矛盾，但前者有时会给出更准确的信息，在第4节介绍例1时解释. 2消除访问路径别名的程序验证方法 2.2程序推理规则的扩展在使用推理规则从语句S的前条件G∧Q产生程序点数据结构构成的形状有多种可能时，则后条件G'∧Q时，要保证Q合法、Q和G无重复和 G表示为G1VG2V…VGm,例如图3(b)的循环不无矛盾变形状图就是G1VG2的形式.同样，Q也可能是先考虑S是指针操作语句，修改指针型数据的 Q1VQ2V…VQm的析取形式，例如第4节例1的简单语句会引起指针值的变化，或者是存储堆块的循环不变式就是Q:VQ2的形式.完整的断言可以增减，因而导致形状图的变化.根据2.1节的介绍可整理成析取范式(disjunctive normal form)G1V 知，对Q的影响是访问路径的替换或者删除部分断 QVG2VQ2V…VGVQ的形式.根据形状图逻言.先假定Q和S无别名，有别名的情况在考虑非辑，可以用析取范式的一种情况为例来讨论，写成G 指针操作语句时介绍.下面分各种语句给出规则. ∧Q,G和Q分别为合取形式. 1)指针型赋值语句u=o 程序验证器基于形状图逻辑进行最强后条件演若u既不是NULL指针也不是悬空指针，则按算并产生验证条件16]，验证条件由Z3自动证明，下面规则得到后断言： 2.1形状图和符号断言之间的联系 {G∧Q}u=w{G'∧Q[u'Iu]}, 符号断言Q中允许出现指针是否等于NULL 其中，G是由形状分析得到的形状图，Q['|]表示或两个指针是否相等的断言.例如在第4节例1的 Q中作为访问路径（包括作为前缀情况）的“及其别循环不变式中，这样的断言用来把其他断言分别联名用和它们相等且不互为别名的访问路径'代换. 系到1r是否等于NULL两种情况.即使函数前后 2)对指针赋值的其他语句条件和循环不变式中没有这样的断言，它们也会因分配空间语句u=malloc(t)和函数调用语句为出现在条件语句或循环语句的布尔表达式中，而 ret=f(act)有关Q的处理同上面赋值语句的规则在最强后条件演算过程中被加到Q中，第4节例1 一样也有这种情况. 3)释放空间语句free(u) Q中指针等于NULL或两个指针相等的断言释放u指向的节点后，Q中含u或u的别名的会因为和G中的信息重复而被吸收，或因有矛盾而原子断言不应再存在，因此规则如下：使得G∧Q为假. (GAQ)free(u)(GAQ), Q中访问路径的合法性依赖于G.例如，在Q中其中，Q'由把Q中含u或“的别名的原子断言都删若出现非指针型的访问路径p->…->data,则忽除而得到略>data所剩下的前缀应该是G上到达某个结构很容易明白，若Q无别名，则这些语句的规则节点的一条访问路径，若是到达悬空节点、NULL 不会导致Q出现别名，因为它们对Q作的小修改都节点或不存在这样的路径则都是非法的，若是到达不会引人别名！谓词节点则视谓词节点展开后的情况决定。再考虑非指针操作语句.只要前断言Q和语句 Q中的访问路径之间是否有别名，Q中的访问 S中无别名，则使用Hoare的赋值公理就是可靠的，路径和下一条语句S中的访问路径之间以及S中若有别名则可以先用G的信息来消除别名（把互为的访问路径之间是否有别名都依赖于G,即利用G 别名的访问路径改成都用其中同一条访问路径)，然可以判断后再用赋值公理.定义函数eliminate._aliases为在指针操作语句中，在对指针赋值时可能会 (S',Q)=eliminate_aliases(G,S,Q),它根据G消

张志天等：一个程序验证器的设计和实现 1049 除S和Q中的别名，得到S和Q' 任何其他变量的值，因此可靠性证明和无别名语言我们把Hoare逻辑的赋值公理限定为无别名的Hoare逻辑的赋值公理的可靠性证明没有区别. 时才能使用，并增加下面的消除别名推理规则： 2)对于指针操作语句，在Q中没有别名的情况 {GΛQ"}S'{GΛQ') 下，这些规则对Q的修改都是可靠的。 {G∧Q}S{G∧Q) 以规则{G∧Q}u=o{G∧Q['Iu]}为例.若一 (S',Q)eliminate_liases(G,S,Q), 条访问路径的前缀被替换，则替换前后的访问路径就可以对含访问路径别名的程序进行推理，指称同一个数据单元.若是一条完整的访问路径被对于修改指针型数据的语句，其前断言Q可能替换，就目前使用的断言语言来说，“只可能作为参是程序员提供的，例如不排除循环不变式中Q存在数出现在链表表长函数length(u,结构体的指针型别名，因此有时也需要这条规则，域名)中（见第4节例1的前断言），用相等的指针复合、条件和循环语句的规则以及推论规则的来代换，则因它们指在同一个节点上而不改变length 形式和Hoare逻辑相应规则的形式一致. 的值. 在没有指针类型的情况下，使用Hoare逻辑的 3)函数eliminate aliases得到的S'和S有同赋值公理从赋值语句的前断言Q得到后断言Q'时，样的语义，Q和Q也有同样的含义.类似2)，消除别不用关心Q是否为Q,VQ2的形式.但是在有指针名前后的访问路径指称同样的数据单元，因此语义类型的情况下，GVG2代表相应程序点的形状图有和含义不变两种可能，需要对它们分别考虑，因此需要增加一条 4)消除别名的推理规则是可靠的.是3)的推论分情况规则： 5)分情况规则的可靠性.在文献[14]中已经 {G1∧Q}S{G1∧Qi}{G2AQ2}S{G2∧Q2} 证明. {G∧QVG2AQ}S{Gi∧Q1VG2∧Q2} 有了这几点则可以说所用的程序逻辑是可靠的. 先前提到的选取析取范式G∧QVG2AQV… VG。AQ.的一种情况来讨论就是基于这条规则. 3 易变数据结构上数据性质的验证方法 2.3程序逻辑的可靠性证明本节简要证明2.2节略加扩展的Hoare逻辑自动程序验证器的验证能力取决于所用的自动对PointerC语言的操作语义是可靠的(sound). 定理证明器的能力，供程序员描述函数前后断言和在有栈和堆的机器上，一个形状图再加上分配循环不变式用的断言语言也是据此来设计的，通用在栈上的整型和布尔型变量的图形表示就构成程序的自动定理证明器一般没有针对易变数据结构的性状态的一种图形表示.这种图形表示的程序状态区质证明的部分，本节介绍如何将所需证明的性质转别于通常状态的主要地方是，每个指针的具体值不化为Z3可以接受的形式. 清楚，但它们之间相等与否是清楚的，因此可以理解易变数据结构上数据性质的描述，例如链表数为每个指针有一个抽象值.基于在这样抽象状态上据的有序性可以通过引人谓词来表示，也可以通过的操作语义，文献[14]证明了下面两个重要性质：使用全称量词来表示，本文设计的验证器采用后者， 1)形状图断言的演算规则是可靠的：例如，可以用下面的断言来描述head所指向的长度 2)形状图逻辑中修改形状图的指针操作语句为m的单链表的有序性：的程序推理规则是可靠的， Yi:1..m-1.(head(->next)->data 有了这两个性质，则2.2节的程序推理规则中， head(>next)i-data). 前后断言中的G和G'是可靠的. 在PointerC的布尔类型表达式的基础上，增加在没有指针类型的情况下，Hoare逻辑的推理带上角标的左值表达式和预定义的用于各种链表的规则对通常的操作语义可靠已是众所周知的.因此函数length,并增加带量词的断言形式，就构成本文下面仅非形式地证明几个涉及扩展的性质，验证器提供的断言语言.为便于阅读，本文描述断言 l)对于非指针操作语句，Hoare逻辑的赋值公所用的逻辑符号并未遵从所设计的断言语言. 理在没有别名的情况下使用是可靠的。本文验证器采用最强后条件演算的方式来产生在无别名的情况下，赋值公理{Q[Ex]}x=E{Q} 验证条件.通常在程序员提供断言的地方会产生验的赋值x=E只改变x的值，不会改变Q中出现的证条件，例如对程序员提供的每个循环不变式会产

1050 计算机研究与发展2013,50(5) 生两个验证条件：循环人口点的断言蕴涵循环不变到相应程序点的形状图G上的信息，因此验证条件式和循环体最后一个语句之后的那个程序点的断言应该是G∧Q→Q,但G上的信息必须符号化.把G 蕴涵循环不变式。上的指针相等（包括指针等于NULL)断言符号化，下面介绍把生成的验证条件提交给Z3时碰到再加上浓缩节点下方的约束断言、链表长度断言（在的3个问题及其解决办法验证条件中出现链表长度断言时需要)，形成符号断 1)把结构体的域名看成函数名，结构体的指针言P,因此实际的验证条件是P∧Q→Q'.若G是空看成函数的变元，以此克服Z3不具备有关访问路图（如不涉及指针类型的程序），则验证条件直接就径的知识带来的困难。是Q→Q'. Bornat在考虑指针程序的证明时，把数据堆看在把指针相等信息符号化时，为避免冗余，给出成由指针索引的一群对象[门，把对象看成由名字索 G上相邻两个静态声明指针变量之间的关系，剩下引的一组成员. 的相等关系可以推导.例如对于图3(b)的第1种情在此采用类似的方式，把结构体的域名看成整况，指针之间的相等关系转换成的符号断言如下：数域上的一元函数名，把结构体的指针当成整型，作 ptrl==head(->next)A ptr==ptrl-> 为函数的变元.例如，第4节例1的结构体类型有两 next A ptrl(>next)"-==NULL, 个域ne.xt和data,它们分别被看成函数.验证条件其中，第3个子断言不用给出，因为经过一个浓缩节中可能有的head->next,ptr->data和ptrl-> 点再指向NULL节点的信息对验证条件的证明通 next->data这样的访问路径分别被翻译成next 常没有用处 (head),data(ptr)data (next(ptr1)).Z3 next 对于双向链表，相邻两个节点之间指向对方的和data当成未解释函数[1町，就是不知其定义的函指针形成一个等式，若域名分别是right和left,则数.若有head==ptrl,则从编程语言的语义知道有p>right>left==p或p>left>right-== head->next==tr1l->ext;在Z3中，若有head== p.那么，代表n个节点的浓缩节点之间就有很多个 ptr1,则从函数的性质也会得出ext(head)== 等式，好在一般来说，当这n个节点在G上被浓缩， next(ptrl). 验证条件就不会涉及其中的指针相等关系，所以在 2)引入辅助的二元函数来克服带上角标的访将G符号化时不用给出这些相等关系。问路径引起的困难。断言中会出现像p(->next)”->data这样带 4 系统原型上角标n并且n可以是线性表达式的访问路径，由于n的值一般不能静态确定，因此该访问路径不可基于形状图逻辑和程序分析的支持，我们实现能翻译成data(next(…next(p)…)并且其中函数了PointerC语言的一个程序验证器[a町，它能够验证 next的应用次数确定的表达式. 不涉及易变数据结构的程序，也能验证涉及各种链可以把p(->next)"翻译成nextn(p,n),并引表和二叉树的构建、插入和删除等的程序.除了验证入一个二元函数nextn(p,n),它基于函数next来定形状外，还能验证节点上数据的一些性质。义（其中n≥0）该验证器无需程序员提供有关数据结构形状的 p,n=0: 函数前后条件和循环不变式，但要求提供非指针型 extn（p,n)=df了ext(p),n=1; 数据的函数前后条件和循环不变式. (next(nextn(p,n-1)),n>1. 4.1系统流程及验证条件的生成显然，nextn(p,n)表达的意思就是p(一> 该验证器分成下面几个模块，按所列次序顺序 next)".在访问路径的表示中，p(->next)+1就是执行 p(>next)"->next;Z3有了函数extn的定义 1)普通编译器的前端后，很容易推出nextn(p,n+1)==next(nextn(p, 对源程序进行词法分析、语法分析和静态语义 n)). 检查后生成抽象语法树， 3)将形状图上的信息用符号断言表示，以支持 2)形状分析验证条件的证明. 遍历抽象语法树，根据形状声明和形状图逻辑符号断言形式的验证条件Q→Q'的证明需要用来生成各程序点的形状图.其中在遇到循环语句时

张志天等：一个程序验证器的设计和实现 1051 需要对它进行多次遍历，以推断循环不变状态图) 入节点后链表保持有序，返回结果链表的指针，代码若整个程序不涉及指针类型，则在每个程序点和断言如图4所示，其中作为链表节点的结构体类生成的是空图型的定义是typedef struct listnode{Node￥：LIST 3)验证条件的生成 next:int data;}Node.该程序不仅涉及形状，而且遍历抽象语法树，根据程序员提供的函数前后需关注各节点数据之间的大小关系。条件和循环不变式，按最强后条件演算方式为各函 Node insert(Node'head.int data) 数生成验证条件. assertion m==length(head,next)A 若仅验证易变数据结构的形状，程序员不用提 Yi:1..m-1.(head(>next)>datahead(>next) 供任何断言，则程序验证在上一步就结束 >data) 下面以4.2节例1为例，说明在本阶段如何将 Node ptr;Node ptrl;Node'ret;Node'p: int j: 分先后得到的G和Q进行对应.在该例中，pr== p=malloc(Node):p->data=data:p->next=NULL; NULL和ptr!=NULL直接出现在程序员提供的 if(head==NULL) 循环不变式的两种情况(Q,VQ2)中，以表示Q和 ret=p: }else if(p>datahead->data) Q2分别联系到ptr是否等于NULL.该循环的循环 p->next=head:ret=p: 不变形状图如图3(b)(G1VG2)所示，r在这两个 else 图上分别表现为等于和不等于NULL.因此，当完 ptrl=head:pir=head->next:j=1: 整的断言(G1VG2)∧(Q1VQ2)展开成析取范式时， while((pir NULL)&(pir->datadata)) loop_assertion 在析取范式的4种情况中，上述tr断言不是因和 ptr NULL A Yi:1..j-1.(head (-next)1 形状图有矛盾而导致该情况被删除，就是因一致而 data 被吸收.这样，在它们被吸收的两种情况中，符号断 head(>next)i->data)A ptrl->datasptr->data 言和与之相适应的形状图就联系在一起， A ptrl->datadata Aj21A Yi:1..m-j-1. pr(next)i-1dataptr(>next)i-data) 4)验证条件的证明 Vptr==NULLA Yi:1..j-1.(head(>next)1 将生成的各验证条件G∧Q→Q',按照第3节 data≤ 所介绍的方法翻译成P∧Q→Q'的形式，逐个交给 head (>next)i->data)A ptrl->data>next:j=j+1; 实际是从Z3证明一(P∧Q→Q)不可满足来得出 } P∧Q→Q成立. p>next=pirl->next:ptrl->next=p;ret=head: 在2.1节提到G中也会有符号断言，G和Q的 } return ret: 符号断言一般不会有矛盾，但G有时会给出更准确 assertion length(ret.next)==m+1A 的信息.在例1中，≤m不能加入循环不变式，因为 yi:1..m.(ret(>next)i-1->dataret(->next)i> 仅j在循环中增1.因此通过最强后条件演算在循 data）环出口点只能得出j≥1，而从G(这时是G1VG2)可以得到j 例1.本例是在有序单链表中插人一个节点，插 datadata A Yi:1..m-1.head (

1052 计算机研究与发展2013,50(5) next)i-->datahead(-next)i-data. 数组类型.下标表达式的使用也会引起别名，例如在在该程序点产生的验证条件是Q蕴涵循环不 i=j时，a[门和a[j门就互为别名.下标变量的别名变式，该验证条件的证明必须在从形状图（如图3 问题比较容易解决，本系统采用的办法是每次对数 (a)所示)获得ptr1==head,ptr==pr1->next和组a的一个下标变量赋值就引入一个大小一样的虚 m一1≥0（该表这时至少有1个节点），还有r== 拟新数组a'(即它仅在验证中使用).例如，若数组a NULLV ptr！=NULL之后才能完成.其他验证条大小是n,在赋值a[]=e(0≤j≤n一1)之后，该赋值的件的证明也需要形状图的支持. 后断言包括其前断言以及Vi:0.j一1.a'[]==a[]N 例2.本例是快速排序的完整程序和断言，如图 a'[j]==e∧Hi:j+1.n-1.a'[i]==a[i]. 5所示.该程序虽不涉及指针型数据，但使用了一维该方法使得生成验证条件的演算比较简单，但 int [10]arr; 增加了自动定理证明器的负担.本例虽然没有给数 int low.up: 组置初值，但它不影响对该程序的验证. int partition(int lowl.int up1) 另一个特点是本例包括了递归函数的验证，以 assertion 0==low Aup==9 A lowk 辑方法相比的优点外，本文方法的另一个优点是，不需要程序员提供有关数据结构形状的函数前后条件 void quick_sort(int low2,int up2){ assertion0==low Aup==9Alom≤lore2A4p2≤wp 和循环不变式，无论是用分离逻辑还是指针逻辑，让 int i: 普通程序员来写这些断言是一件十分困难的事情. if(low2<up2) 另外，分离逻辑用分离合取连接词来分隔不同 i=partition(low2.up2): quick_sort(low2.i-1):quick_sort(i+1.up2); 堆块的断言的方式，使得一般需要引入归纳定义的谓词来描述数据结构的节点之间的关系.而与归纳 return: 定义相适应的是用递归方式而不是循环方式来编 assertion0==low Aup==9∧lor≤loe2A lomw2≤up2A"p2≤upA Yi:lo2..up2-1.a[门≤a[i+1] 程，例如文献[22]给出的研究程序验证的源语言连循环语句也没有.对于各种链表的插入和删除等函 main() 数，程序员可能更习惯用循环来编程，本文给出的带 assertion true low=0:up=9:quick_sork(low.up): 上角标的访问路径以及使用全称量词的方式，便于 assertion 0==low Aup==9A Yi:low..up-1.a[i]a[i+1] 描述各种链表的节点之间的数据关系。分离逻辑的优势是其适用性较强，它不需要像 Fig.5 Program and assertions of the Quicksort function. 本文这样禁止编程语言使用指针算术运算和取地址图5快速排序完整的程序和断言运算等.分离逻辑技术的众多研究使得它在提高自

张志天等：一个程序验证器的设计和实现 1053 动化程度[2]、终止性证明2)、细粒度的并发、基 [6]Barnett M.Rustan M.Leino M.et al.The spec# 于锁的并发性[2们和用于Java语言[2)等方面有很大 programming system:An overview [G]//LNCS 3362:Proc of Int Workshop Construction and Analysis of Safe,Secure. 拓展.除了用于源程序的验证以外，本文方法在其他 and Interoperable Smart Devices (CASSIS 2004).Berlin: 方面的应用有待进一步研究. Springer.2004:49-69 [7]Flanagan C.Leino K R M.Lillibridge M.et al.Extended 6总结 static checking for Java [C]//Proc of the Conf on Programming Language Design and Implementation (PLDI'02).New York:ACM.2002:234-245 本文提出一种利用形状图信息来消除访问路径 [8]Berdine J.Calcagno C.O'Hearn P W.Smallfoot:Modular 别名，使得指针程序仍然可以用Hoare逻辑来进行 automatic assertion checking with separation logic [G]/ 验证的方法，并利用可满足性模理论求解器Z3的 LNCS 4111:Proc of Formal Methods for Components and 支持，开发了一个PointerC语言的程序验证器原 Objects(FMCO 2005).Berlin:Springer.2005:115-137 [9]Distefano D.Parkinson M J.jStar:Towards practical 型，展示了该方法的可行性 verification for Java [C]//Proc of ACM SIGPLAN Int Conf 本文方法的局限是程序员只能使用有限的几种 on Object-Oriented Programming.Systems.Languages.and 形状来编程.下一步考虑怎样以现有的几种形状为 Applications (OOPSLA 2008).New York:ACM.2008: 基础，构造出各种所需的形状，例如嵌套的形状（例 213-226 如双向链表的每个节点指向一个单链表)、带有附加 [10]Carter G.Monahan R.Morris J M.Software refinement with perfect developer [C]//Proc of the 3rd IEEE Int Conf 链的形状（把形状上满足某个性质的节点链接起 on Software Engineering and Formal Methods(SEFM 2005). 来)、增加附加指针的形状（例如在二叉树的每个节 Piscataway.NJ:IEEE.2005:363-372 点上增加指针形成左孩子右兄弟树). [11]Reynolds J C.Separation logic:A logic for shared mutable 我们将继续寻找减轻自动定理证明器负担的方 data structures [C]//Proc of the 17th Annual IEEE Symp on Logic in Computer Science LICS 2002).Piscataway.NJ: 法.目前正在实现的是：提供程序员在断言中使用自 IEEE.2002.55-74 定义谓词以及表达不同自定义谓词之间关系的机 [12]Berdine J.Calcagno C.O'Hearn P W.A decidable fragment 制.仍以易变数据结构为例，允许程序员在断言中使 of separation logic [G]//LNCS 3328:Proc of the 24th Int 用自定义谓词，除了可以比较简洁地表示节点之间 Conf on Foundations of Software Technology and Theoretical Computer Science(FSTTCS 2004).Berlin:Springer.2004: 的数据关系外，联系不同谓词的关系等式是相关验 97-109 证条件的证明依据和提示。 [13]Moura L D.Bjorner N.Z3:An efficient SMT solver [G]/ LNCS 4963:Proc of Conf on Tools and Algorithms for the 参考文献 Construction and Analysis of Systems (TACAS 2008). Berlin:Springer.2008 [1]Lin Huimin.Zhang Wenhui.Model checking:Theory. [14]Li Zhaopeng.Zhang Yu.Chen Yiyun.Shape graph logic and a shape system [OL].[2012-12-05].http://ssg.ustcsz. methods and applications [J].Acta Electronica Sinica.2002. edu.cn/SGL 30(12A):1907-1912(in Chinese) [15]Liu Gang.Chen Yiyun.Zhang Zhitian.Automatic inference (林惠民，张文辉.模型检测：理论、方法与应用[门.电子学 of loop invariant shape graphs [J].Chinese Journal of 报，2002,30(12A):1907-1912) Electronic Technology.2011(8):4-6 (in Chinese) [2]Hoare CA R.An axiomatic basis for computer programming (刘刚，陈意云，张志天.循环不变形状图的自动推断[J门， []Communications of the ACM.1969.12(10):576-585 电子技术，2011(8)：4-6) [3]Paulson L C.Isabelle:A Generic Theorem Prover [M]. [16]Necula G.Proof-carrying code [C]//Proe of the 24th ACM Berlin:Springer.1994:1-300 Symp on Principles of Programming Languages(POPL'97). [4]The Coq Development Team.The Coq proof assistant New York:ACM.1997:106-119 reference manual.Version 8.2 [OL].[2009-08-01].http:// [17]Bornat R.Proving pointer programs in Hoare logic [G] cog.inria.fr LNCS 1837:Proc of the 5th Int Conf on Mathematics of [5]Aleksandar N.Morrisett G.Shinnar A.et al.Ynot: Program Construction(MPC 2000).Berlin:Springer.2000: Dependent types for imperative programs [C]//Proc of the 102-126 13th ACM SIGPLAN Int Conf on Functional Programming [18]Kroening D.Strichman O.Decision Procedures:An (ICFP'08).New York:ACM.2008:229-240 Algorithmie Point of View [M].Berlin:Springer,2008