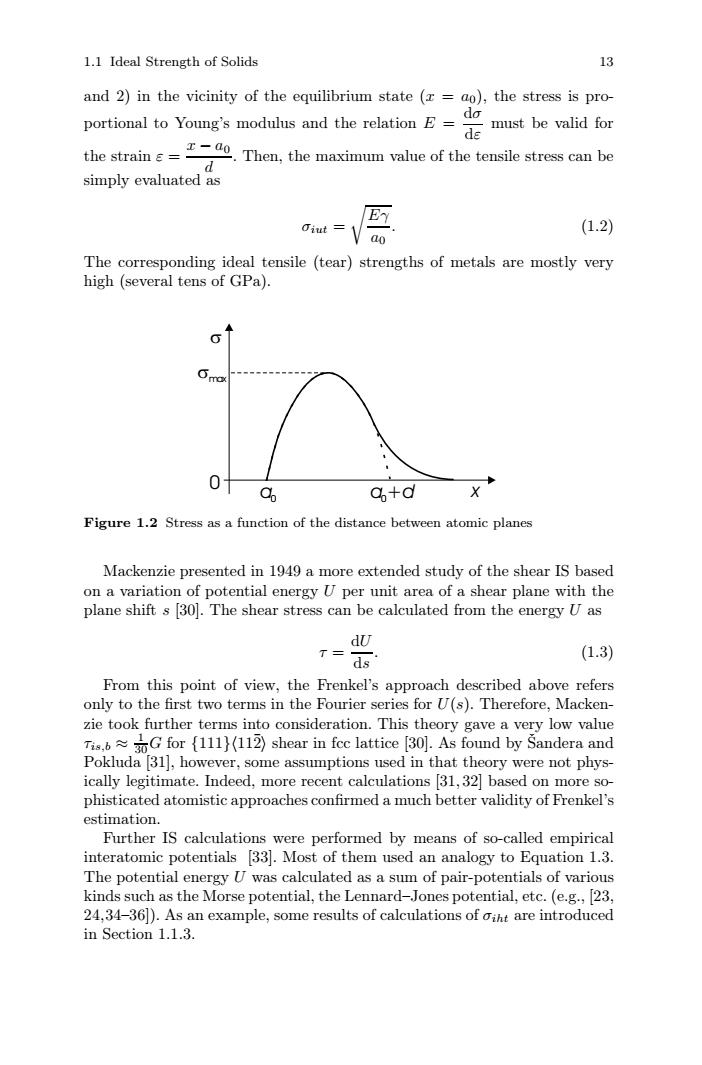
1.1 Ideal Strength of Solids 13 and 2)in the vicinity of the equilibrium state (x =ao),the stress is pro- do portional to Young's modulus and the relation E de must be valid for the strain e o.Then,the maximum value of the tensile stress can be d simply evaluated as E (1.2) ao The corresponding ideal tensile (tear)strengths of metals are mostly very high(several tens of GPa). 0 a6 &+d X Figure 1.2 Stress as a function of the distance between atomic planes Mackenzie presented in 1949 a more extended study of the shear IS based on a variation of potential energy U per unit area of a shear plane with the plane shift s [30].The shear stress can be calculated from the energy U as dU T= (1.3) ds From this point of view,the Frenkel's approach described above refers only to the first two terms in the Fourier series for U(s).Therefore,Macken- zie took further terms into consideration.This theory gave a very low value sG for {111)(112)shear in fcc lattice [30].As found by Sandera and Pokluda [31],however,some assumptions used in that theory were not phys- ically legitimate.Indeed,more recent calculations 31,32 based on more so- phisticated atomistic approaches confirmed a much better validity of Frenkel's estimation. Further IS calculations were performed by means of so-called empirical interatomic potentials [33].Most of them used an analogy to Equation 1.3. The potential energy U was calculated as a sum of pair-potentials of various kinds such as the Morse potential,the Lennard-Jones potential,etc.(e.g.,23, 24,34-361).As an example,some results of calculations of oiht are introduced in Section 1.1.3.1.1 Ideal Strength of Solids 13 and 2) in the vicinity of the equilibrium state (x = a0), the stress is pro￾portional to Young’s modulus and the relation E = dσ dε must be valid for the strain ε = x − a0 d . Then, the maximum value of the tensile stress can be simply evaluated as σiut = Eγ a0 . (1.2) The corresponding ideal tensile (tear) strengths of metals are mostly very high (several tens of GPa). a0 x 0 max a0+d Figure 1.2 Stress as a function of the distance between atomic planes Mackenzie presented in 1949 a more extended study of the shear IS based on a variation of potential energy U per unit area of a shear plane with the plane shift s [30]. The shear stress can be calculated from the energy U as τ = dU ds . (1.3) From this point of view, the Frenkel’s approach described above refers only to the first two terms in the Fourier series for U(s). Therefore, Macken￾zie took further terms into consideration. This theory gave a very low value τis,b ≈ 1 30G for {111}11¯2 shear in fcc lattice [30]. As found by Sandera and ˇ Pokluda [31], however, some assumptions used in that theory were not phys￾ically legitimate. Indeed, more recent calculations [31, 32] based on more so￾phisticated atomistic approaches confirmed a much better validity of Frenkel’s estimation. Further IS calculations were performed by means of so-called empirical interatomic potentials [33]. Most of them used an analogy to Equation 1.3. The potential energy U was calculated as a sum of pair-potentials of various kinds such as the Morse potential, the Lennard–Jones potential, etc. (e.g., [23, 24,34–36]). As an example, some results of calculations of σiht are introduced in Section 1.1.3.