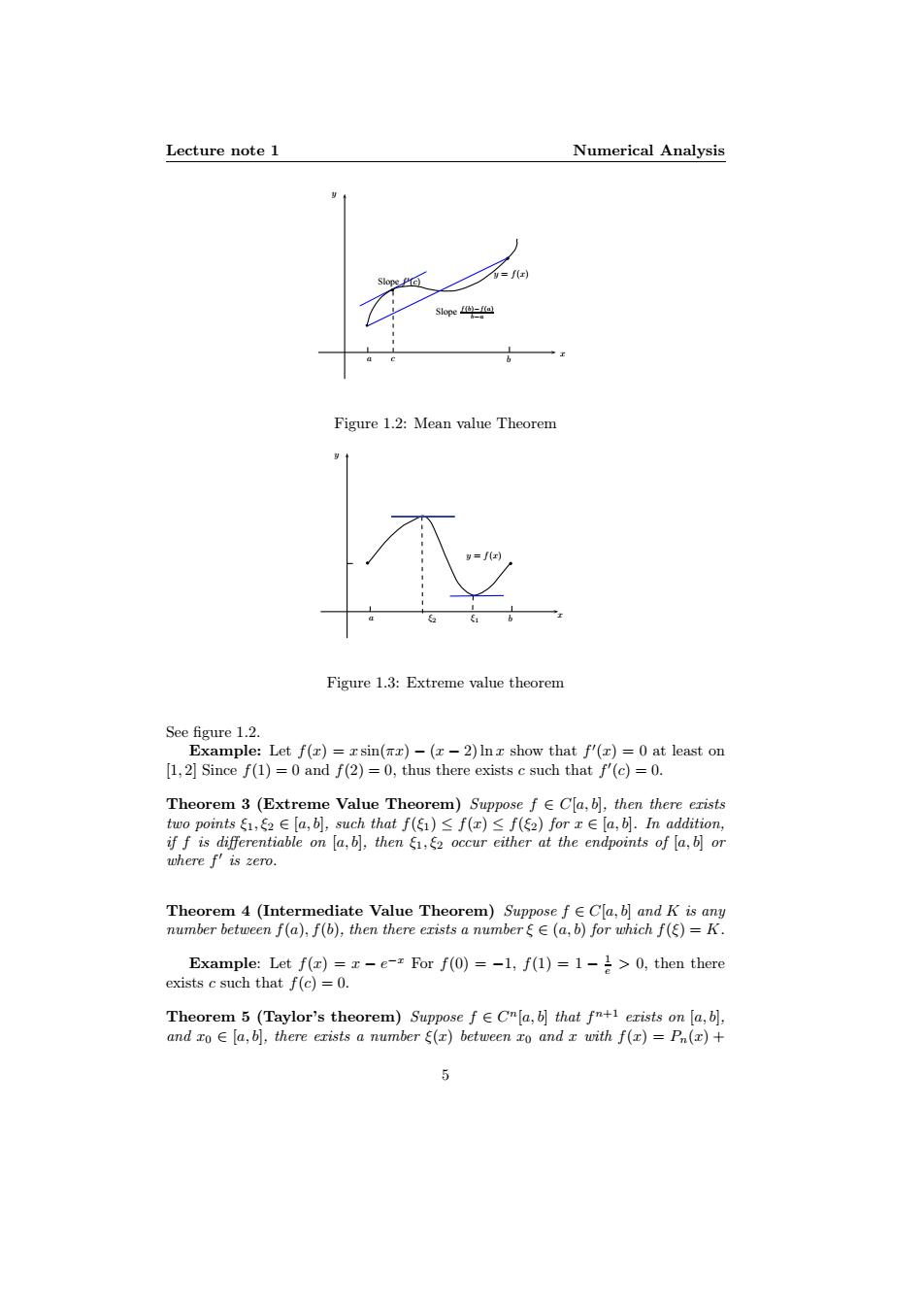
Lecture note 1 Numerical Analysis f(r) Slope) Slope Figure 1.2:Mean value Theorem Figure 1.3:Extreme value theorem See figure 1.2. Example:Let f(x)=xsin(x)-(x-2)Inx show that f'(x)=0 at least on [1,2]Since f(1)=0 and f(2)=0,thus there exists c such that f'(c)=0. Theorem 3(Extreme Value Theorem)Suppose f ECla,b],then there erists two points E,2∈[a,bl,such that f()≤f(x)≤f(ξ2)forx∈[a,.In addition, if f is differentiable on [a,b],then E,2 occur either at the endpoints of a,bl or where f'is zero. Theorem 4(Intermediate Value Theorem)Suppose f E Cla,b]and K is any number between f(a),f(b),then there exists a numbergE(a,b)for which f()=K. Example:Let f(x)=x-e-z For f(0)=-1,f(1)=1-1>0,then there exists c such that f(c)=0. Theorem 5(Taylor's theorem)Suppose fCn[a,b]that fn+1 erists on [a,b], and ro E [a,b],there erists a number E(r)between ro and r with f(r)=Pn(x)+Lecture note 1 Numerical Analysis b b a c b y = f(x) b Slope f ′ (c) Slope f(b)−f(a) b−a x y Figure 1.2: Mean value Theorem b b a ξ2 b y = f(x) x y ξ1 Figure 1.3: Extreme value theorem See figure 1.2. Example: Let f(x) = x sin(πx) − (x − 2) ln x show that f ′ (x) = 0 at least on [1, 2] Since f(1) = 0 and f(2) = 0, thus there exists c such that f ′ (c) = 0. Theorem 3 (Extreme Value Theorem) Suppose f ∈ C[a, b], then there exists two points ξ1, ξ2 ∈ [a, b], such that f(ξ1) ≤ f(x) ≤ f(ξ2) for x ∈ [a, b]. In addition, if f is differentiable on [a, b], then ξ1, ξ2 occur either at the endpoints of [a, b] or where f ′ is zero. Theorem 4 (Intermediate Value Theorem) Suppose f ∈ C[a, b] and K is any number between f(a), f(b), then there exists a number ξ ∈ (a, b) for which f(ξ) = K. Example: Let f(x) = x − e −x For f(0) = −1, f(1) = 1 − 1 e > 0, then there exists c such that f(c) = 0. Theorem 5 (Taylor’s theorem) Suppose f ∈ C n[a, b] that f n+1 exists on [a, b], and x0 ∈ [a, b], there exists a number ξ(x) between x0 and x with f(x) = Pn(x) + 5