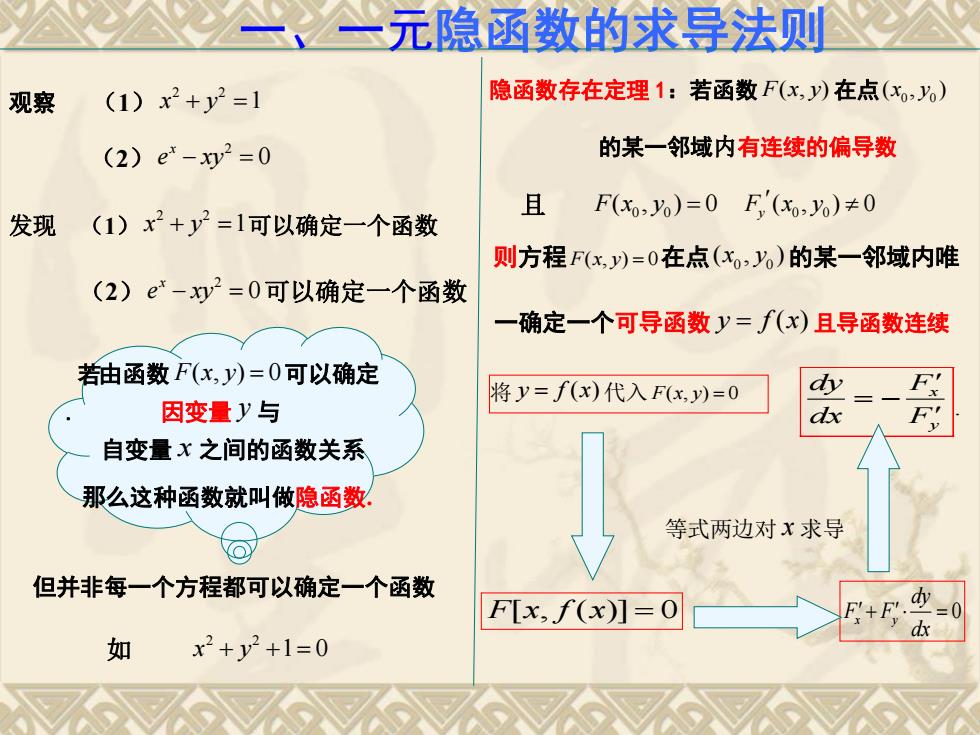
一元隐函数的求导法则 观察 (1)x2+y2=1 隐函数存在定理1：若函数F(x,)在点(x,) (2)e*-xy2=0 的某一邻域内有连续的偏导数 且 F(x,%)=0F,'(xo,%)≠0 发现 (1)x2+y2=1可以确定一个函数 则方程F(x,)=0在点(x,)的某一邻域内唯 (2)e-y2=0可以确定一个函数 一确定一个可导函数y=f(x)且导函数连续 若由函数F(x,y)=0可以确定 将y=(x)代入F(x,y)=0 dy__ 因变量y与 dx 自变量x之间的函数关系 那么这种函数就叫做隐函数， @ 等式两边对x求导 但并非每一个方程都可以确定一个函数 F[x,f(x)]=0 +Ek .=0 如 x2+y2+1=0 一、一元隐函数的求导法则 观察 （1） 2 2 x y  1 （2） 2 0 x e xy   发现 （1） 2 2 x y  1可以确定一个函数 （2） 2 0 x e xy   可以确定一个函数 但并非每一个方程都可以确定一个函数 如 2 2 x y   1 0 由函数 F x y ( , ) 0  可以确定 . 因变量 y 与 自变量 x 之间的函数关系 那么这种函数就叫做隐函数. 隐函数存在定理 1：若函数 F x y ( , ) 在点 0 0 ( , ) x y 的某一邻域内有连续的偏导数 且 0 0 F x y ( , ) 0  0 0 ( , ) 0 F x y y   则方程F x y ( , ) 0  在点 0 0 ( , ) x y 的某一邻域内唯 一确定一个可导函数 y f x  ( ) 且导函数连续 将 y f x  ( ) 代入 F x y ( , ) 0  F x f x [ , ( )] 0  等式两边对 x 求导 0 x y dy F F dx      x y dy F dx F     . 若