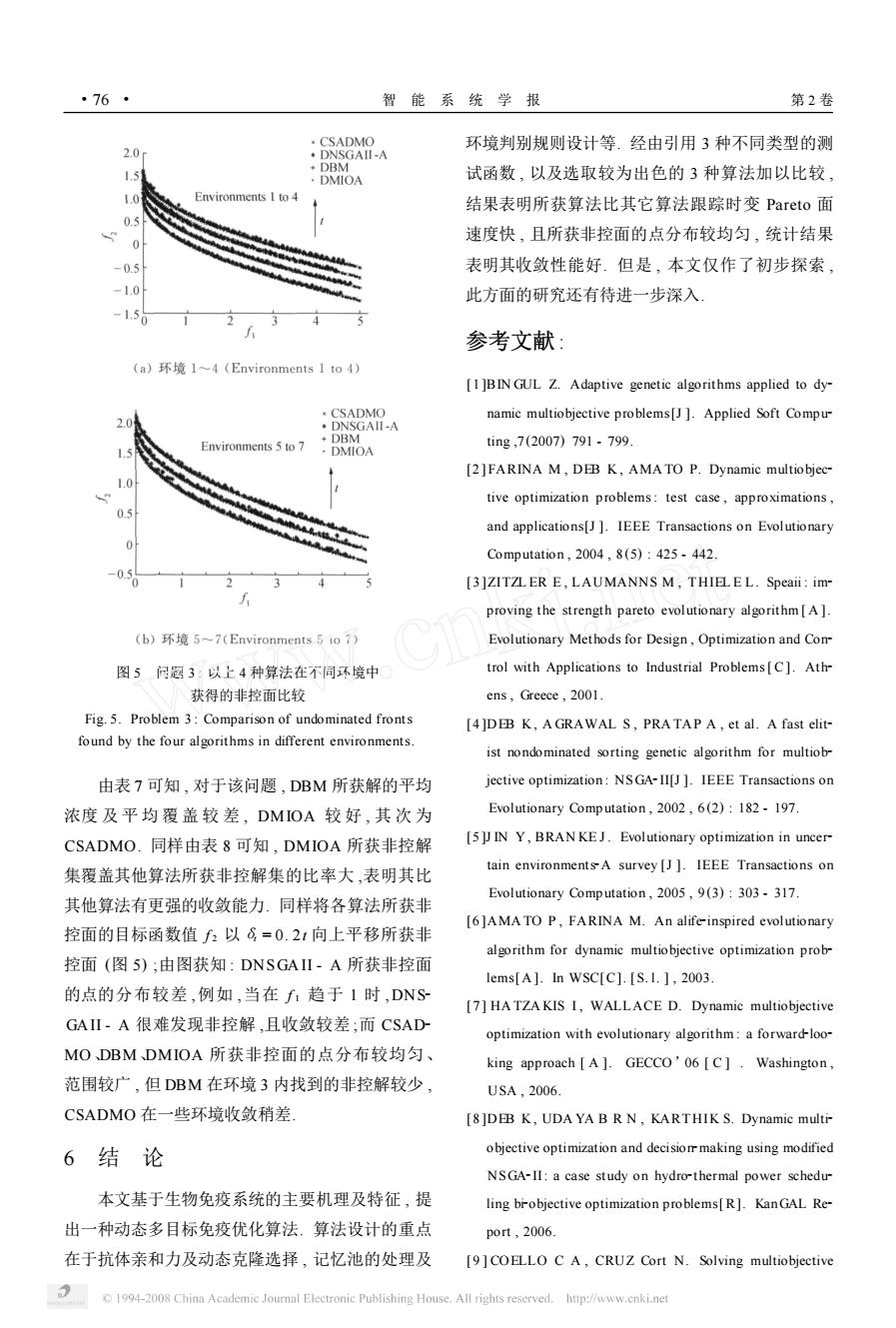
·76· 智能系统学报 第2卷 CSADMO 环境判别规则设计等.经由引用3种不同类型的测 2.0 ·DNSGAII-A 1.5 DBM ·DMIOA 试函数，以及选取较为出色的3种算法加以比较， 1.0 Environments I to 4 结果表明所获算法比其它算法跟踪时变Pareto面 0.5 速度快，且所获非控面的点分布较均匀，统计结果 0 -0.5 表明其收敛性能好.但是，本文仅作了初步探索， -1.0 此方面的研究还有待进一步深入 参考文献： (a)环境1~4(Environments1to4) [1]BIN GUL Z.Adaptive genetic algorithms applied to dy- CSADMO namic multiobjective problems[J].Applied Soft Compu ·DNSGAII-A Environments 5 to 7 DBM ting,7(2007)791-799 ·DMIOA [2]FARINA M,DEB K,AMATO P.Dynamic multiobjec- tive optimization problems:test case,approximations, and applications[J ]IEEE Transactions on Evolutionary Computation,2004,8(5):425.442. (3]ZITZL ER E,LAUMANNS M,THIELEL.Speaii:im- proving the strength pareto evolutionary algorithm[A]. (b)环境5~7(Environments5to7) Evolutionary Methods for Design,Optimization and Con- 图5问题3：以上4种算法在不同环境中 trol with Applications to Industrial Problems [C].Ath 获得的非控面比较 ens,Greece,2001. Fig.5.Problem 3:Comparison of undominated fronts [4]DEB K,A GRAWAL S,PRATAP A,et al.A fast elit- found by the four algorithms in different environments. ist nondominated sorting genetic algorithm for multiob- 由表7可知，对于该问题，DBM所获解的平均 jective optimization:NSGA-II[J ]IEEE Transactions on 浓度及平均覆盖较差，DMIOA较好，其次为 Evolutionary Computation,2002,6(2):182-197. CSADMO.同样由表8可知，DMIOA所获非控解 [5J IN Y,BRANKEJ.Evolutionary optimization in uncer- 集覆盖其他算法所获非控解集的比率大，表明其比 tain environmentsA survey [J].IEEE Transactions on Evolutionary Computation,2005,9(3):303-317 其他算法有更强的收敛能力.同样将各算法所获非 [6]AMA TO P,FARINA M.An alife-inspired evolutionary 控面的目标函数值f2以6=0.2t向上平移所获非 algorithm for dynamic multiobjective optimization prob- 控面（图5）；由图获知：DNSGAII-A所获非控面 lems[A].In WSC[C].[S.1.]2003. 的点的分布较差，例如，当在f1趋于1时，DNS [7]HA TZA KIS I,WALLACE D.Dynamic multiobjective GAⅡ-A很难发现非控解，且收敛较差；而CSAD optimization with evolutionary algorithm:a forward-loo- MO DBM DMIOA所获非控面的点分布较均匀、 king approach [A ]GECCO'06 [C].Washington, 范围较广，但DBM在环境3内找到的非控解较少， USA,2006. CSADMO在一些环境收敛稍差 [8]DEB K,UDA YA B R N,KARTHIK S.Dynamic multi- 6结论 objective optimization and decisiomaking using modified NSGA-II:a case study on hydro-thermal power schedu- 本文基于生物免疫系统的主要机理及特征，提 ling br-objective optimization problems[R].KanGAL Re- 出一种动态多目标免疫优化算法.算法设计的重点 p0rt,2006. 在于抗体亲和力及动态克隆选择，记忆池的处理及 [9]COELLO C A,CRUZ Cort N.Solving multiobjective 1994-2008 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net图 5 问题 3 : 以上 4 种算法在不同环境中 获得的非控面比较 Fig. 5. Problem 3 : Comparison of undominated fronts found by the four algorithms in different environments. 由表 7 可知 , 对于该问题 , DBM 所获解的平均 浓度 及 平 均 覆 盖 较 差 , DMIOA 较 好 , 其 次 为 CSADMO. 同样由表 8 可知 , DMIOA 所获非控解 集覆盖其他算法所获非控解集的比率大 ,表明其比 其他算法有更强的收敛能力. 同样将各算法所获非 控面的目标函数值 f 2 以δt = 0. 2t 向上平移所获非 控面 (图 5) ;由图获知 : DNSGAII - A 所获非控面 的点的分布较差 ,例如 ,当在 f 1 趋于 1 时 ,DNS2 GAII - A 很难发现非控解 ,且收敛较差 ;而 CSAD2 MO、DBM、DMIOA 所获非控面的点分布较均匀、 范围较广 , 但 DBM 在环境 3 内找到的非控解较少 , CSADMO 在一些环境收敛稍差. 6 结 论 本文基于生物免疫系统的主要机理及特征 , 提 出一种动态多目标免疫优化算法. 算法设计的重点 在于抗体亲和力及动态克隆选择 , 记忆池的处理及 环境判别规则设计等. 经由引用 3 种不同类型的测 试函数 , 以及选取较为出色的 3 种算法加以比较 , 结果表明所获算法比其它算法跟踪时变 Pareto 面 速度快 , 且所获非控面的点分布较均匀 , 统计结果 表明其收敛性能好. 但是 , 本文仅作了初步探索 , 此方面的研究还有待进一步深入. 参考文献 : [1 ]BIN GUL Z. Adaptive genetic algorithms applied to dy2 namic multiobjective problems[J ]. Applied Soft Compu2 ting ,7 (2007) 791 - 799. [2 ] FARINA M , DEB K , AMA TO P. Dynamic multiobjec2 tive optimization problems: test case , approximations , and applications[J ]. IEEE Transactions on Evolutionary Computation , 2004 , 8 (5) : 425 - 442. [3 ]ZITZL ER E , LAUMANNS M , THIEL E L. Speaii : im2 proving the strength pareto evolutionary algorithm[ A ]. Evolutionary Methods for Design , Optimization and Con2 trol with Applications to Industrial Problems[ C]. Ath2 ens , Greece , 2001. [4 ]DEB K , A GRAWAL S , PRA TAP A , et al. A fast elit2 ist nondominated sorting genetic algorithm for multiob2 jective optimization : NSGA2II[J ]. IEEE Transactions on Evolutionary Computation , 2002 , 6 (2) : 182 - 197. [5 ]J IN Y, BRAN KE J. Evolutionary optimization in uncer2 tain environments2A survey [J ]. IEEE Transactions on Evolutionary Computation , 2005 , 9 (3) : 303 - 317. [6 ]AMA TO P , FARINA M. An alife2inspired evolutionary algorithm for dynamic multiobjective optimization prob2 lems[A ]. In WSC[C]. [ S. l. ] , 2003. [7 ] HA TZA KIS I , WALLACE D. Dynamic multiobjective optimization with evolutionary algorithm : a forward2loo2 king approach [ A ]. GECCO’06 [ C ] . Washington , USA , 2006. [ 8 ]DEB K , UDA YA B R N , KARTHIK S. Dynamic multi2 objective optimization and decision2making using modified NSGA2II: a case study on hydro2thermal power schedu2 ling bi2objective optimization problems[ R]. KanGAL Re2 port , 2006. [9 ] COELLO C A , CRUZ Cort N. Solving multiobjective · 67 · 智 能 系 统 学 报 第 2 卷