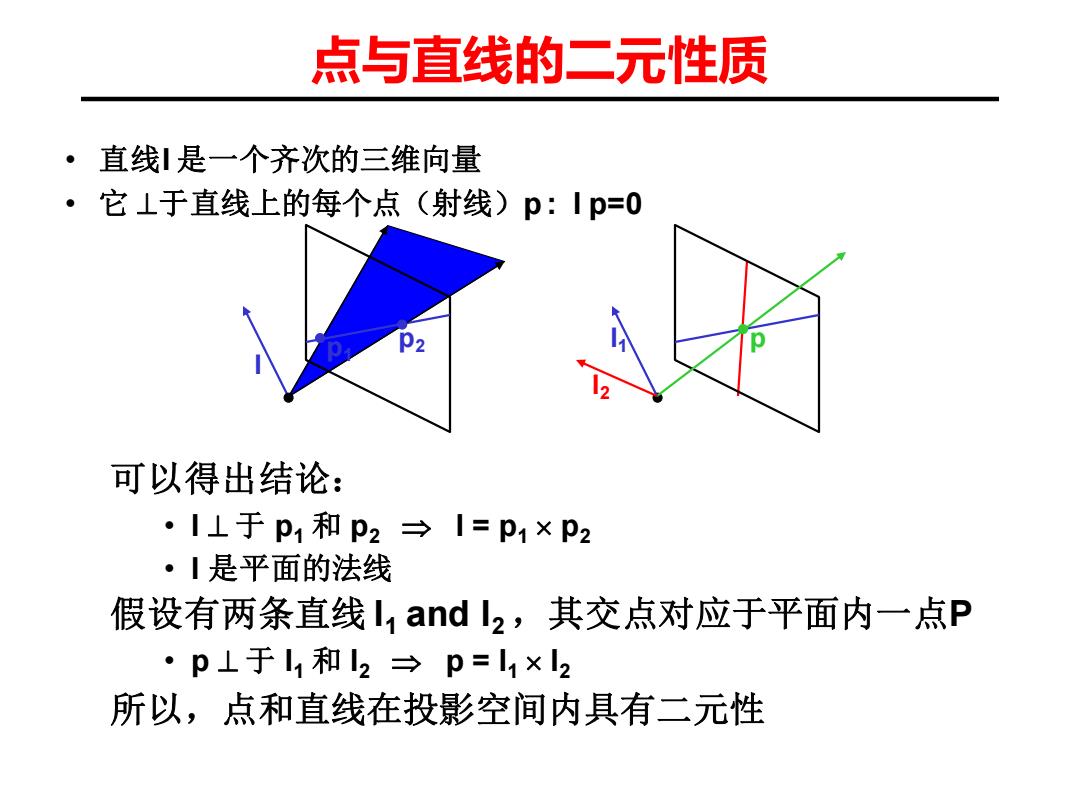
点与直线的二元性质 ·直线！是一个齐次的三维向量 ·它⊥于直线上的每个点（射线）p:Ip=0 可以得出结论： ·I⊥于p1和p2→I=P1×P2 ·I是平面的法线 假设有两条直线l1and2,其交点对应于平面内一点P ·p⊥于l1和2→p=l1×l2 所以，点和直线在投影空间内具有二元性l 点与直线的二元性质 • 直线l 是一个齐次的三维向量 • 它 ⊥于直线上的每个点（射线）p : l p=0 p1 p2 假设有两条直线 l1 and l2 ，其交点对应于平面内一点P • p ⊥ 于 l1 和 l2  p = l1  l2 所以，点和直线在投影空间内具有二元性 l1 l2 p 可以得出结论： • l ⊥ 于 p1 和 p2  l = p1  p2 • l 是平面的法线