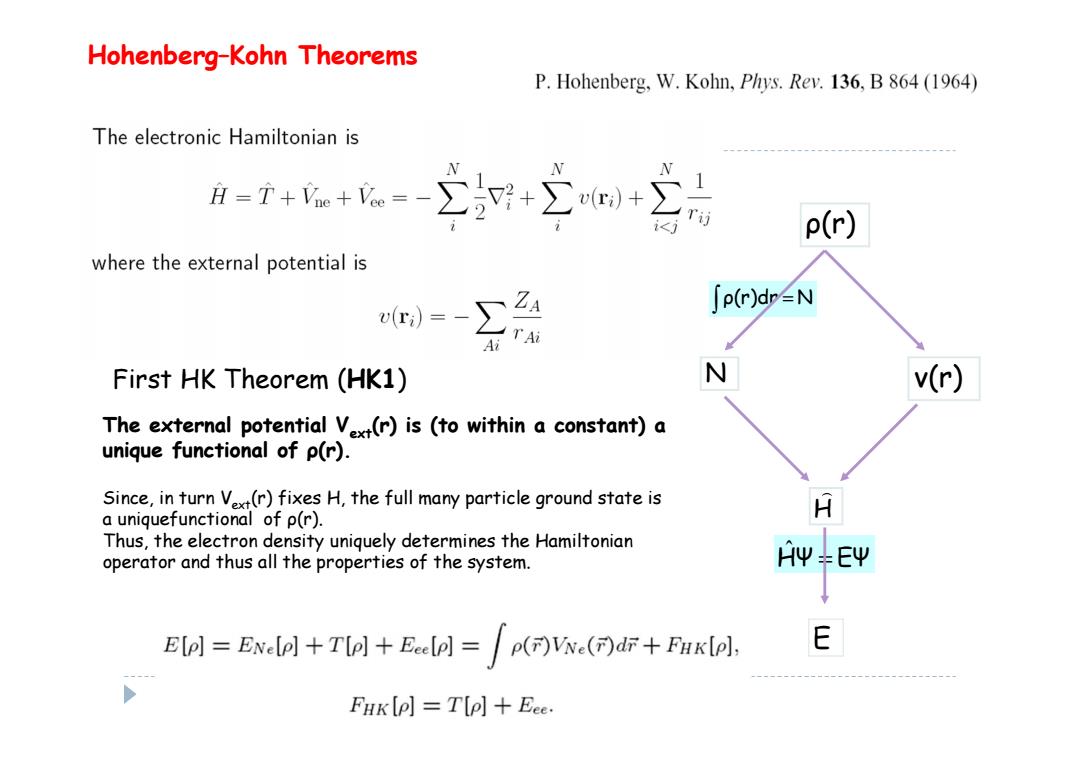
Hohenberg-Kohn Theorems P.Hohenberg,W.Kohn,Phys.Rev.136,B 864 (1964) The electronic Hamiltonian is A=T++=-∑+∑+ i p(r) where the external potential is r)=-∑24 ∫p(rdr2N Ai T Ai First HK Theorem (HK1) N v(r) The external potential Vx(r)is (to within a constant)a unique functional of p(r). Since,in turn Vext(r)fixes H,the full many particle ground state is a uniquefunctional of p(r). A Thus,the electron density uniquely determines the Hamiltonian operator and thus all the properties of the system. AΨ+EΨ Elo]=ENe+Tol+Eeeel =()Vx()dr+Fuklol, E FHK (P]T(p]Eeeρ(r) ν(r) H  E N  ρ(r)dr = N HΨ = EΨ ˆ First HK Theorem (HK1) Hohenberg–Kohn Theorems The external potential Vext(r) is (to within a constant) a unique functional of ρ(r). Since, in turn Vext(r) fixes H, the full many particle ground state is a uniquefunctional of ρ(r). Thus, the electron density uniquely determines the Hamiltonian operator and thus all the properties of the system