
第七章:密度泛函理论方法 Chapter 7 DFT
第七章:密度泛函理论方法 1 Chapter 7 DFT

Why DFT Density Functional Theory (DFT) DFT is an alternative approach to the theory of electronic structure; electron density plays a central role in DFT. Why a new theory? HF method scales as N4 (N -of basis functions) Cl methods scale as N6-N10 MPn methods scale as >N5 CC methods scale as >N6 >Correlated methods are not feasible for medium and large sized molecules!
Why DFT Density Functional Theory (DFT) DFT is an alternative approach to the theory of electronic structure; electron density plays a central role in DFT. Why a new theory? HF method scales as N4 (N - # of basis functions) CI methods scale as N6-N10 MPn methods scale as >N5 CC methods scale as >N6 Correlated methods are not feasible for medium and large sized molecules!
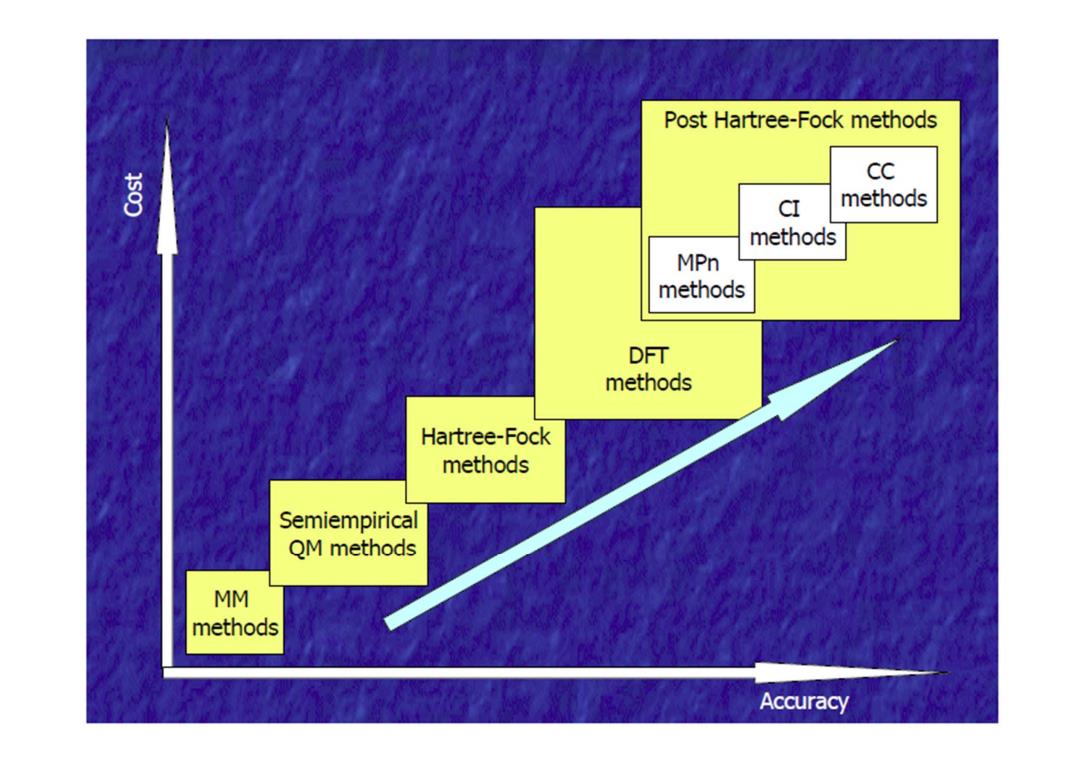
Post Hartree-Fock methods CC 1500 cI methods methods MPn methods DFT methods Hartree-Fock methods Semiempirical QM methods MM methods Accuracy

Background 1920s:Introduction of the Thomas-Fermi model. 1964:Hohenberg-Kohn paper proving existence of exact DF. 1965:Kohn-Sham scheme introduced. 1970s and early 80s:LDA.DFT becomes useful. 1985:Incorporation of DFT into molecular dynamics(Car-Parrinello) (Now one of PRL's top 10 cited papers). 1988:Becke and LYP functionals.DFT useful for some chemistry. 1998:Nobel prize awarded to Walter Kohn in chemistry for development of DFT
Background 1920s: Introduction of the Thomas-Fermi model. 1964: Hohenberg-Kohn paper proving existence of exact DF. 1965: Kohn-Sham scheme introduced. 1970s and early 80s: LDA. DFT becomes useful. 1985: Incorporation of DFT into molecular dynamics (Car-Parrinello) (Now one of PRL’s top 10 cited papers). 1988: Becke and LYP functionals. DFT useful for some chemistry. 1998: Nobel prize awarded to Walter Kohn in chemistry for development of DFT

Basic Theory:The electron density is the essential Probability of finding electron 1 in dx1,electron 2 in dx2,...electron N in dxN: |Ψ(x1,x2,…,xw)l2dx1dx2.dxw Integrating over the space and spin coordinates of electron 2,3,...,N and the spin coordinate of electron 1 one obtaines the probability of finding electron 1 in volume element dr whilst the other electrons are anywhere: (-∫axz.w)Pdsa.dwan Multiplying by N one obtaines the probability of finding any electron in dr1: v(-∫lw,x,xw)Ids.dxzdxx)ah=p)an The quantity p(r1)is the electron density: v-6 .)ds,dx…dw
Basic Theory: The electron density is the essential

Properties of the electron density p()is a non-negative function depending on only three variables .p()vanishes at infinity and integrates to the total number of electrons N: limp()=0 →0 p(di=N p()can be measured experimentally (e.g.by X-ray diffraction) at the position of atoms,the gradient of p()has a discontinuity: l层+2z6=0 Z being the nuclear charge and p()the spherical average of p() decays exponentially for large distances from nuclei p()~exp(-2v2) I being the exact first ionization energy of the system Function:y=f(x) p=p(xy,Z) Functional:y=F[f(x)] E=F[p(x,y,z)]
Properties of the electron density Function: y=f(x) ρ = ρ(x,y,z) Functional: y=F[f(x)] E=F[ ρ(x,y,z)]
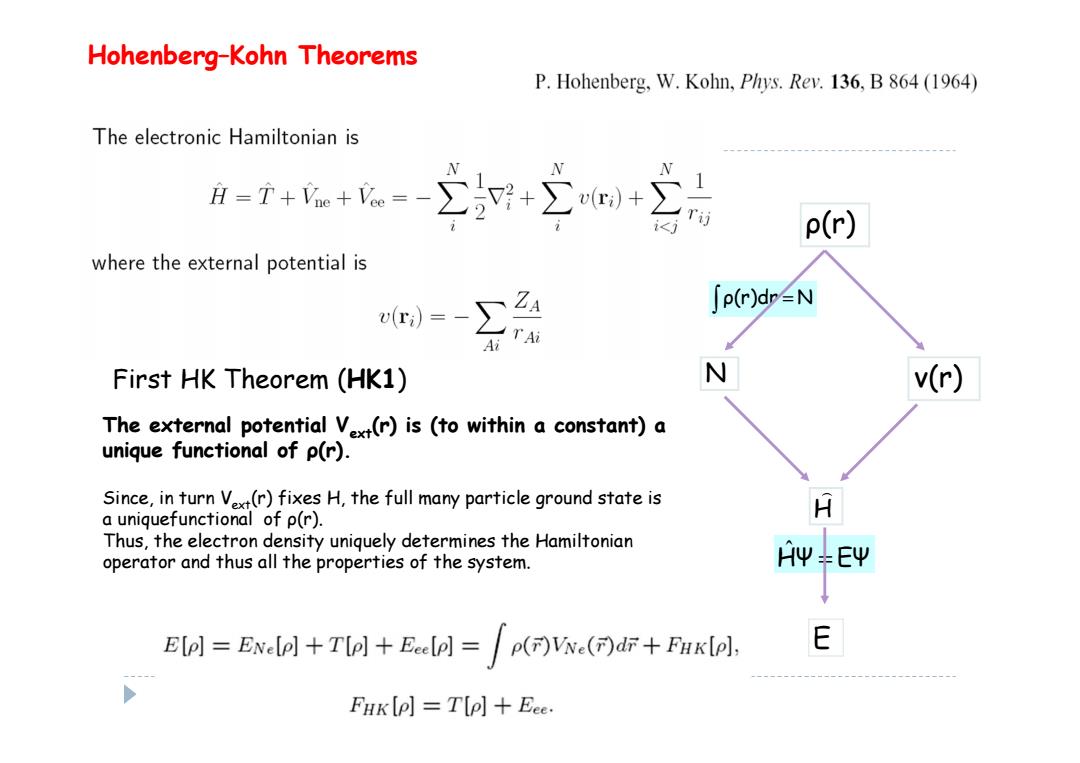
Hohenberg-Kohn Theorems P.Hohenberg,W.Kohn,Phys.Rev.136,B 864 (1964) The electronic Hamiltonian is A=T++=-∑+∑+ i p(r) where the external potential is r)=-∑24 ∫p(rdr2N Ai T Ai First HK Theorem (HK1) N v(r) The external potential Vx(r)is (to within a constant)a unique functional of p(r). Since,in turn Vext(r)fixes H,the full many particle ground state is a uniquefunctional of p(r). A Thus,the electron density uniquely determines the Hamiltonian operator and thus all the properties of the system. AΨ+EΨ Elo]=ENe+Tol+Eeeel =()Vx()dr+Fuklol, E FHK (P]T(p]Eee
ρ(r) ν(r) H E N ρ(r)dr = N HΨ = EΨ ˆ First HK Theorem (HK1) Hohenberg–Kohn Theorems The external potential Vext(r) is (to within a constant) a unique functional of ρ(r). Since, in turn Vext(r) fixes H, the full many particle ground state is a uniquefunctional of ρ(r). Thus, the electron density uniquely determines the Hamiltonian operator and thus all the properties of the system

A=T+V+Va→平→D←平=F=T+V+V 儿 E 国 Proof: 4'as a test function for H: E。< (平'平= =ΨΨ+(平-Ψ E。< E6+(Ψ'T+Ve+Vet-i-Ve-V|平 E。< E+p(F){Ves-Ves}dr Y as a testfunction for H': Eo<Eo-p(F)[Ves-Ves}dr Summing up the last two inequalities: E+E%<E+E。 Contradiction!
Ψ’ as a test function for H: Ψ as a testfunction for H’: Summing up the last two inequalities: Proof: Contradiction!

Eo[Po]=T[Po]+Eee[Po]+ENe[Po]. Eo[Po]=|Po(F)VNedi T[Po]+Eee[Po] system dependent univgfsally valid Eo[Po]=Po()VNedi +Fik[po] FHk??? Fak[p]=T[p]+E.[p]=(T+Vw E1-50@+5l=+E的

E[p]=ENe [p]+T[p]+Eee [p]=p(r)VNe (F)dr +FK[p] with f4K[pl=I可 Eee -打8d+5回5西 Only J[p]is known! The explicit form of T[p]and EnnLp]is the major challenge of DFT contains all the effects of self-interaction correction and exchange and Coulomb correlation