
物质波的统计规律--M.Born1926 对应于空间的一个状态,就有一个 伴随这状态的德布罗依波的几率。 若与电子对应的波函数在空间某点 为零,这就意味着在这点发现电子 第一讲:回顾 的几率小到零。 一波恩 量子力学: 从量子力学产生到双原子分子体系电子结构 波动性 可亚加性,不需要物理量在空间的分布 电子的波动性控制电子在不同区域出现的几率! 4 量子力学的产生 旧量子论:波尔原子结构模型(1913年) -Bohr's Theory:Quantization Energy of H Atom(1913) energy.The electron loses energy only when it jumps between the allowed orbits and the atoms emits this energy as light of a given wave length. ·定春规则:电子运动于一组德定的圆周轨道 (定态),原子在定态中不发射也不吸 43 收电磁辐射能。其角动量满足如下的量子化 月2 条件:L=h/2)=n ●频率条件:电子从一个定态轨道跃 物质是否无限可分? 迁到另外一个轨道时,会以电磁波的形 经典力学理论是否适用于微观粒子 式放出(或吸收)能量hv=|Em-E.| 5 从经典力学到量子力学 波粒二象性束缚态电子:定态→驻波 经典理论 Newton's Law de BroglieSchrodinger: Maxwell's Eg. 撒观粒子的定态与驻波对应 1=2l/m,n=1,2,3.. 氢原子的圆形电子轨道的驻波条件: 黑体辐射旧量子论 新量子论 光电效应 能量量子 轨道周长=波长整数倍 康普领散射 微观粒子量子化 光的量子化 ).h/p 氢原子光谱 波尔理论 被的粒子性 粒子的波动性物质波 2πa=n1=nh/p s=hy 电子散射 角动量 波粒二象性 p=h/A L=ap=nh/(2n)=nh 不确定原理 量子力学 6 1
1 第一讲:回顾 从量子力学产生到双原子分子体系电子结构 量子力学的产生 2 物质是否无限可分? 经典力学理论是否适用于微观粒子 从经典力学到量子力学 Newton’s Law Maxwell’s Eq. 经典理论 黑体辐射 旧量子论 新量子论 3 能量量子 光的量子化 旧量子论 微观粒子量子化 新量子论 波的粒子性 粒子的波动性 量子力学 黑体辐射 光电效应 康普顿散射 氢原⼦光谱 波尔理论 物质波 h 电⼦散射 波粒⼆象性 p h / 不确定原理 物质波的统计规律 --- M. Born 1926 对应于空间的一个状态,就有一个 伴随这状态的德布罗依波的几率。 若与电子对应的波函数在空间某点 为零 这就意味着在这点发现电子 4 , 的几率小到零。 ——波恩 量子力学: 波动性 可叠加性,不需要物理量在空间的分布 电子的波动性 控制 电子在不同区域出现的几率! —— Bohr’s Theory: Quantization Energy of H Atom (1913) 定态规则:电子运动于一组稳定的圆周轨道 原子在定态中不发射也不吸 Assumption: There are certain allowed orbits for which electron has a fixed energy. The electron loses energy only when it jumps between the allowed orbits and the atoms emits this energy as light of a given wave length. 旧量子论:波尔原子结构模型(1913年) 5 (定态),原子在定态中不发射也不吸 收电磁辐射能。其角动量满足如下的量子化 条件: L = nh/ (2π)=nћ 频率条件:电子从一个定态轨道跃 迁到另外一个轨道时,会以电磁波的形 式放出(或吸收)能量 hv = | Em – En | de Broglie和Schrodinger: 微观粒子的定态与驻波对应 氢原子的圆形电子轨道的驻波条件: λ = 2l / n, n = 1, 2, 3… l 波粒二象性 束缚态电子:定态驻波 轨道周长=波长整数倍 λ = h / p 2 π a = n λ = n h / p L = a p = n h / (2π) = n ћ 角动量 6

R.H.Fowler,L.Brillouin, 态叠加原理 P.Debye,M.Knudsen.W.L.Bragg.H.A.Kramers.P.A.M.Dirac. 意兵成具有可套知技:从不同成甜睡麦出的局列放,春有业地在 AH CO L.de Broglie.M.Born.N.Bohr 女河种婚,在老幻南通的显成。声鱼的放骑成两个被的业加。南 函两列使有和网的频平和围走的位和基,就★声业干步。 ·态叠加原理:若,丝,是体系可能的状态,则它 们线性叠加所得的波函数 y=c4+c42+…+cwn=∑c 也是体系的一个可能状态:当体系处于态时,出现 4:的概率由C∑,c给出:或者说,体系部分处于 ,29。中. 两一个电子的不同状春可以叠加 波函数 薛定谔方程 1926年Born提出了波函数的统计解释,指出波函数的绝对值平 波函数是态函数 体系性质完全由其决定 →问题:如何得到波函数? 方代表发现粒子的几率密度 平,t) 1.某一时刻,某一地点,粒子出现 力学量算符(Operator) 的概率正比于该时刻、该地点波 函数模的平方1,t)。Ψ p→-0:p→-i 0△r 2.1ct)P是概率密度,1r,tPdr 为体积元r发现该粒子的概率 T→ 2 3. 有物理意义的是引红,P,而不是 2m r,)。 几率被里(正,t) ”我潮”,而不是"来巴有之” E→防⊙ 0t 波函数的性质 波函数的统计解释对波函数的要求 单粒子含时薛定谔方程 1.归一性: [lv(r.nfd'r=1 2 若加(.r=C,则称为归一化常数 品7,刘= 2+Mw(7,) 2.常数因子不定:华与。华描述微粒的同一个状态 = w(,t) 3.相位因子不定:少与。◆”描述微粒的同一个状态 -Erwin Schrodinger,1926 4.品优特性:单值、有限、连续 1.华是单值的时问和空问的单值函数 量乎方季的一个基本服走,不可证明。 2.华是连续的Ψ及其一级微商(坐标)是时问和空问的连续函数 3.心是有限的(平方可积) 2
2 1929 1922 1932 1933 1933 1954 7 1918 1921 波函数 1926年Born提出了波函数的统计解释,指出波函数的绝对值平 方代表发现粒子的几率密度 1. 某一时刻,某一地点,粒子出现 的概率正比于该时刻、该地点波 8 2. |Ψ(r,t)| 2 是概率密度, |Ψ(r,t)| 2 d3r 为体积元 d3r 发现该粒子的概率 几率波 “预期”,而不是“本已有之” 函数模的平方 |Ψ(r,t)| 2= Ψ*Ψ 3. 有物理意义的是|Ψ(r,t)| 2 ,而不是 Ψ(r,t)。 波函数的性质 波函数的统计解释对波函数的要求 2. 常数因子不定:Ψ 与 c Ψ 描述微粒的同一个状态 1. 归一性: 相位因子不定 与 iφ 描述微粒的同 个状态 9 3. 相位因子不定:Ψ 与 eiφΨ 描述微粒的同一个状态 4. 品优特性:单值、有限、连续 2. Ψ 是连续的 Ψ及其一级微商(坐标)是时间和空间的连续函数 3. Ψ 是有限的 (平方可积) 1. Ψ 是单值的 时间和空间的单值函数 经典波具有可叠加性: 从不同波动源发出的两列波,各自独立地在 空间传播,在它们相遇的区域,产生的波动是这两个波的叠加。如 果两列波有相同的频率和固定的位相差,就会产生干涉。 态叠加原理 10 同一个电子的不同状态可以叠加 薛定谔方程 力学量算符 (Operator) 波函数是态函数 问题:如何得到波函数? 体系性质完全由其决定 11 t E i m T i x p i p i x 2 2 2 : , 单粒子含时薛定谔方程 12 量子力学的一个基本假定,不可证明

定态薛定谔方程 *系事婚不上台对润V(行,)=V(行) 49 本征函数与本征值 ·分离变量yt)=pr)0,代入h兴=w 26 再两边同时除以(红,) h0.1-足+r回回 Ψ(x)= Sin n f(t)at (r)2m ·左边只是时间函数,右边只是的函数→共同常数E E= 2π2h2 求解时间部分,可得f(t)=e 2ma2 n=1,2,3 定态薛定博方程 方2 2m v+V)w(F)=Ew(F) 13 N粒子体系 应用:离域键的形成 13丁二烯(C=C-C=C键长为a) 2m 8ma -Σ乐6小 ·模型1:两个孤立双键 0 E=46=2m ·模型2:一个离域大π键 0 Ao({》= +∑.oa=Eo》 2m, =25+5)=0+45 4m(3a36 E'm<E,易于形成大π键 14 17 定态薛定谔方程一势箱中的粒子 三维势箱中的粒子 0 (0<x<a,0<y<b,0<:<c) 一维势箱中的粒子 V(x) V(x,八,)= (others) (无限深势阱,束缚态) 哈密顿量 A= 2,82 2m)+V(xy) 势函数 四 0 薛定得方程 (0<x<d 户w(x八,)=Ew(x,y,) V(x)= (x2a,x≤0) 波函数分离变量 w(x,y,)=w(x)w2(y)w3() 0 8 史志菁史污女程 月=-龙d2 2m+" 本征西数与本征值 2m ,%,,八3=L2,… 3
3 定态薛定谔方程 V(r,t) V(r) 如果势场不显含时间 2 i f t 1 13 1 2 2 i f t V ft t m r r r • 左边只是时间函数,右边只是r的函数 共同常数E ( ) ( ) ( ) 2 2 2 V r r E r m 定态薛定谔方程 N粒子体系 2 , 2 i tot ij i j i ij i p E V rr m 14 2 2 ˆ , 2 i i ij i j i i i ij i H r V rr r E r m V(x) I II III 一维势箱中的粒子 (无限深势阱,束缚态) 定态薛定谔方程 —— 势箱中的粒子 势函数 x 0 a ( , 0) 0 (0 ) ( ) x a x x a V x 15 ( ) 2 ˆ 2 2 2 V x dx d m H 定态薛定谔方程 sin 2 ( ) n 本征函数与本征值 16 1, 2, 3... 2 ( ) sin 2 2 2 2 n ma n E x a a x n n 应用:离域键的形成 • 模型1:两个孤立双键 17 • 模型2:一个离域大 键 ( ) 0 (0 , 0 , 0 ) ( , , ) others x a y b z c V x y z ( ) ( , , ) 2 ˆ 2 2 2 2 2 2 2 V x y z m x y z H 哈密顿量 ( ) ( ) 薛定谔方程 Hˆ E 三维势箱中的粒子 薛定谔方程 H (x, y,z) E (x, y,z) ( , , ) ( ) ( ) ( ) 1 2 3 波函数分离变量 x y z x y z 18 , , , 1,2, 2 ( ) sin sin sin 8 ( , , ) 1 2 3 2 2 2 2 3 2 2 2 2 2 1 , , 1 2 3 , , 1 2 3 1 2 3 n n n c m n b n a n E z c n y b n x a n abc x y z n n n n n n 本征函数与本征值

简并度 a-b=c E π2清2 2ma四+店+ 单电子体系一氢与类氢原子体系 以2,Ψ2,Ψ2 → E=6 哈密顿量 2ma2 A=- 2 能量是三重简并 111→12121L112→221212122-→31L13113→. r元-I 中心力场V) 4定态问题 简并 波函数(RR) 体系的某一个能量值,对应着若干个不同的波函数 简并的出现与体系的对称性有关 告 1 +Borm-0 ppenheimer近似(BO,绝热近似) 考虑电子运动时,视核近似不动 高对称性的体系往往出现能级简并 19 算符 定义 户人=五 三个量子数 二超鞏是上k故: 算符即运算规则。它作用在一个函数了上即是对∫ 0,1,2,3,4) 进行某种运算,得到另一个函数 侧一球量于廉,球场中分晨(亿ma放应) (m不同,1相周的状本,在藏师中有不同的德量) 能级简并度: 厄米算符 对任意品优波函数,算符清足g(y,)dr=(yjy,dr 被西数 w.xR(r)er(0yD(o) 则F是厄米算符 9,8,p)=n(m) E.a(+ouh 角动量算符 量子算符定义: 径向面收 R0-r∑ 卫,上。有共同的本征雷表暴 人·疏,m-0,士L,,同s) 障0及安外,有n-1-1个径向节点。R(r)=0 20 量子力学基础一小结 原子轨道分布图 量子论的实验基础、德布罗意-受因斯坦关暴、测不准关系 The Orbitron gallery of atomic orbitals 波西数(波西墩的线计解驿、标准条件、自由电子的波西数) 06 算符(乘法和对易、本征方程、常见的力学量算符(坐标、动量、角 0 动量、能量等)) 线性算符、厄密算符的定义和性质 ⊙.8 Schrodinger2方寝(定态、含时) 势箱中粒子的定态解(能量、被西敷) 0.6.8 被通数放力学量本征面数系展开,力学量的可测值和几率、平均懂 0.08年.的.●8 对易力学量(供同本征西敢系、测不准关) . e 88.60 轨道角动量(定义、对易关系、本征方程及其解) g 路80 4
4 ( ) 2 2 3 2 2 2 2 1 2 2 , , 1 2 3 n n n ma En n n a=b=c 112 121 211 , , 2 2 2 2 6 ma E 能量是三重简并 简并度 19 简并 体系的某一个能量值,对应着若干个不同的波函数 简并的出现与体系的对称性有关 高对称性的体系往往出现能级简并 111121,211,112221,212,122311,131,113 算符 定义 算符即运算规则。它作用在一个函数 f1 上即是对 f1 进行某种运算,得到另一个函数 f2 1 2 ˆ F f f 厄米算符 20 对任意品优波函数,算符满足 则 是厄米算符 F 角动量算符 量子算符定义: L Lz ˆ , ˆ2 有共同的本征函数系 , 0, 1, , ( ) Lz m m lml 量子力学基础 —— 小结 量子论的实验基础、德布罗意-爱因斯坦关系、测不准关系 波函数(波函数的统计解释、标准条件、自由电子的波函数) 算符(乘法和对易、本征方程、常见的力学量算符(坐标、动量、角 动量、能量等)) 线性算符、厄密算符的定义和性质 21 Schrodinger方程(定态、含时) 势箱中粒子的定态解 (能量、波函数) 波函数按力学量本征函数系展开,力学量的可测值和几率、平均值 对易力学量(共同本征函数系、测不准关系) 轨道角动量(定义、对易关系、本征方程及其解) 单电子体系 -- 氢与类氢原子体系 r Ze M m H e e N 0 2 2 2 2 2 2 2 4 哈密顿量 | | 22 e N r r r 中心力场V(r) 波函数 定态问题 1836 1 M me Born-Oppenheimer近似(BO, 绝热近似) n —— 主量子数,壳层 K,L,M,N l —— 角量子数,支壳层 s,p,d, f, g (0,1,2, 3,4 ) m —— 磁量子数,磁场中分裂(Zeeman效应) (m不同n,l 相同的状态,在磁场中有不同的能量) 三个量子数 能级简并度: 2 1 g (2 1) n n (未考虑电子自旋) 2 1 E 23 0 gn (2 1) n 未考虑电子自旋 2 n En 波函数 nm (r,,) n m E m H L L n z 2 2 ( 1) ˆ ˆ ˆ ( ) ( ) () m m n m n R r 径向函数 0 1 0 n l Zr na l j nl j j R r e r br 原子轨道分布图 24

自旋 近似方法 1925年,Uhlenbeck与Goudsmit提出电子具有一个 类氢原子模型一零级近似(完全忽略电子间作用) intrinsic(built-.in)角动量 单电子近似(轨道近似) 经验屏蔽常数法(Slater轨道) 如果我们将电子看成一个球:-Spim ,自洽场(SCF)方法 两电子体系为例 “Spin“不是一个经典效果、旋转模型并不是真实的物理现象 自旋是所有粒子的基本内桌属性之一 一吉-者awm网 的作酒 电子是费米子,自旋量子数是1/2 总红三长m- ⑧,$)具有共同的本征函数,其本征值: 总A画A四 s+12,s=0..1.3.… 小@en用人n m九,m,=-多,-+L,,s一1,s e美,Ja'amn 28 全同粒子 变分原理 经典世界 量子世界 设中。为任何一个满足体系边界条件的近似基态波函数,测近似基态能量(能 量期待值): 斯-之g 'odr 户体系的Hamilton算符 E。真正的基态修量milton算符的最低的能量本征值) 88 用任问近似基态波函数所计算的能量期特值总是大于真正的基态能量。 望电=低可风小 确定的轨迹 不确定原理 为过度的丽(国2安分添结】,中一气原可路后 全同粒子可区分 全同粒子不可区分 -/电电 电子总被函最必须是交换反对称 Slater行列式 bo.o.v.(w) 124N 15 单原子体系一小结 多电子原子与变分法 ()核和电子被视为点粒子。 氢原子和类氢离子的能级和波函数、量子数的物理意义、 (仅仅考德核与电子、电子与电子之间的静电(库仑)相互作用, 忽略础相互作用或其它相对论效应。 波函数的图形表示 (ii)假定核不动。(Bor-Oppenheim Approximation,1927) B-O近似、单电子近似、中心力场近似的基本思想 Hamilton Operator 变分原理、简单多电子原子的变分法处理 ÷1- N 7 N i= 电子自旋(自旋量子数、自旋磁矩)、全同性原理 2 +∑1 多电子波函数的构成、行列式波函数 月-立0+22 ◆27 5
5 自旋 1925年,Uhlenbeck与Goudsmit提出电子具有一个 intrinsic(built-in)角动量 如果我们将电子看成一个球:---Spin “Spin” 不是一个经典效果 旋转模型并不是真实的物理现象 25 、旋转模型并不是真实的物理现象 自旋是所有粒子的基本内禀属性之一 电子是费米子,自旋量子数是1/2 S ) ˆ S , ˆ( z 2 具有共同的本征函数,其本征值: 全同粒子 经典世界 量子世界 26 确定的轨迹 全同粒子可区分 不确定原理 全同粒子不可区分 P N P N N N Nq N q q P N N N N N N ( ) 2 (2) 1 (1) ˆ ( 1) ! 1 (1) (2) ( ) (1) (2) ( ) (1) (2) ( ) ! 1 (1,2, , ) 1 2 2 2 2 1 1 1 电子总波函数必须是交换反对称 Slater行列式 多电子原子与变分法 (i) 核和电⼦被视为点粒⼦。 (ii)仅仅考虑核与电⼦、电⼦与电⼦之间的静电(库仑)相互作⽤, 忽略磁相互作⽤或其它相对论效应。 (iii)假定核不动。(Born-Oppenheim Approximation, 1927) 27 Hamilton Operator N i N i N i i j i ij i r r Z H 1 11 2 1 2 1 ˆ N i N i N j i ij r H h i 1 1 ( ) ˆ ˆ i i r Z h i 2 2 1 ( ) ˆ 近似方法 类氢原子模型 – 零级近似 (完全忽略电子间作用) 单电子近似(轨道近似) 经验屏蔽常数法(Slater轨道) 自洽场(SCF)方法 28 变分原理 设 为任何一个满足体系边界条件的近似基态波函数,则近似基态能量(能 量期待值): 0 0 0 0 0 0 0 ˆ E d H d W Hˆ 体系的Hamilton算符 E0 真正的基态能量 (Hamilton算符的最低的能量本征值) 用任何近似基态波函数所计算的能量期待值总是大于真正的基态能量。 29 单原子体系 —— 小结 氢原子和类氢离子的能级和波函数、量子数的物理意义、 波函数的图形表示 B-O近似、单电子近似、中心力场近似的基本思想 30 变分原理、简单多电子原子的变分法处理 电子自旋(自旋量子数、自旋磁矩)、全同性原理 多电子波函数的构成、行列式波函数

双原子体系与线性变分法 线性变分法 5、久期方程 氨分子离子H2+ A=--E-2+1 2m G万R 久期方程组: ∑间,-6,=0i=1,n LCAO:Linear Combination ofAtomic Orbitals 将久期方程组可为矩库形式(但。一S…H.一5. 生果靠近a核。女近杜为以:图靠近b核,y近似为 (H-S)C=0 H-…H_- 中间区域。近似为两者找性叠加:y=cu。+Ca 是一个关于个未知数的线性方程组,根据线性代数的知识,有非学解的必受条件 问题:如何确定系数G和仁,?)线性变分法 是系数行列式为零,于是有解条件为: 镜:。为尝试变分雨数。马和马等为变分参数 dct▣-=0 决定体系的物量 -→Ee上w'vdr/[v'ud: 之求解{何}的线性方程切 果蒙方超组 久湘方塑 变静条n(证在,)=0 ∑(H。-Es)=0 ES 》34 线性变分法 线性变分法 1).变分原理: 世iozE det H-S =0 了pdr 赶 ,一定有m个实根,我们记这个根作为体罩的■个最低的 变分法: 中=中o(a,2,…,an) a为位置参数 6=6。≤61≤6≤£d 形=@l)/@Φ) =Wa,4,a.) 会a40 ↓↓↓↓ E。E1EEn- i=0,…,m 2).线性变分函数 对于每一个能最:可代回久期方程想,求出恒合系敢: v=立c月 考意一姐调足边界条件的已知图数(信卧),它们慎性无关且归一化:何,华,}】 。→6,}→”。=∑丹近似的基态波函数 警试麦分通歌选为这姐已知通数的城性姐合 爱m elj=ln 有→,}→叫,=∑网,近似的第一激发态波函最 变分壶数为粗合系数: 这种变分法票为此性变分法, 2 35 线性变分法 线性变分法 3引、能量表达式 6)、求解思路 g=∑c%之E= Σsaed西 →H ∑Σ,网9 (1首先由问圆的体系边界条件越操一姐已知西数由体暴哈密领可计算积分(称 矩阵元) 选积分 ,=lp,)s=》 (迅)解久期方程: detH-=0 得▣个能量近似值: E=6,6n (丝)年个或解得组合数。即得近似波西重! f+t=1n (H-S)C=0 %-20 6
6 双原子体系与线性变分法 氢分子离子H2 + LCAO: Linear Combination of Atomic Orbitals 1 , 1 br s b e 2 22 2 1 ˆ 2 a b e e H m rrR 31 线性变分法 0 ˆ E d H d 1). 变分原理: 变分法 : ( , , , ) 0 0 1 2 m ˆ W0 0 H 0 0 0 ( , , , ) 0 1 2 Wo m αi 为位置参数 32 ( , , , ) W0 1 2 m ( ) 1 2 o m i i 0,,m 2). 线性变分函数 考虑一组满足边界条件的已知函数(基函数),它们线性无关且归一化:1n 尝试变分函数选为这组已知函数的线性组合: j n j j c 1 变分参数为组合系数: c j j 1,....n 这种变分法称为线性变分法。 线性变分法 3)、能量表达式 重迭积分 33 线性变分法 5)、久期方程 久期方程组: 0 j ij ij j S c i 1,,n 将久期方程组写为矩阵形式 11 11 1 1 1 0 n n S S c (Η S)C 0 34 0 n1 n1 nn nn n S S c 是一个关于n个未知数的线性方程组,根据线性代数的知识,有非零解的必要条件 是系数行列式为零,于是有解条件为: det Η S 0 决定体系的能量 系数方程组 久期方程 线性变分法 det Η S 0 由于系数矩阵厄米对称,一定有n个实根,我们把这n个根作为体系的n个最低的 能量近似值(能量的上限): 0 1 2 1 .... n E E E E 35 E0 E1 E2 En1 对于每一个能级,可代回久期方程组,求出组合系数: j n j j c 1 j j j j 0 c0 0 c0 近似的基态波函数 j j j j 1 c1 1 c1 近似的第一激发态波函数 线性变分法 6)、求解思路 (ⅰ)首先由问题的体系边界条件选择一组已知函数,由体系哈密顿可计算积分(称 矩阵元) ij i j ˆ Sij i j (ⅱ) 解久期方程 36 解久期方程: det Η S 0 得n个能量近似值: n , ....., 1 (ⅲ) 每个 k 解得组合系数,即得近似波函数: k ckj j 1,....n (Η S)C 0 j j k kj c

分子体系理论要点 分子体系理论要点 1)分子S方程 4)LCAO-MO近似 分子的薛定诗方程: Φ=s中 分子轨道取为某些合理的原子轨道的线性组合: 分子体系的波函数 中=(,视】 g=2c0 分子体系的肠miltonian算符 月=f+i+++ 对干含个电子,量个核的分子体系: 似}为原子轨道(实际上只能是近似的原子轨道)。 ®岁缸心竖岁贸 (注意:原子轨道问不一定相互正交)。 :恢的质量(原子单位】。Z核电荷数. 组合系数{C,}由变分法或其他方法确定。 2)Borm-Oppenheimeri近似 (,成(,风》=,视) 枝的质量比电子烦量大得多 w=c1.(1s)+c2(1s)+cp(2s)+c%(2s)+ 中(,)=Ψ(,Wx() 持的网电子动骨过好并处理 经提-个样7的电的分.越-个电有6中 37 40 分子体系理论要点 分子体系理论要点 Continuing... MO法的基本近似: 从面将电子站动和枝运网分离。 ⑦.++=Ψ ⑦.+牌,=c-E座 1、非相对论近似 (1)电子达网方程: 五Ψ▣E 电子装函数是电子坐标的而数,同时索最绝依验于族坐标的变化:里。=平(:说) 电子能量象数地于坐标韵变化:£(:》 2、B-0近似 敏子化学的株心州题粮是求解如上电子贴对方程! 2)特运动方程: i平.-cΨx 3、轨道近似(单电子近似) 电子能随转坐标的变化加上族枝排斥胸成族运对的务影。中尼)》称野能国面。 出小婚根是一个春常好的话缸月龙的调地象常人与为解我多电子问愿心烟吴用的其他无缸阳比。其演她调常可以8不。 建于毫动内宽动的板互角两《电子同隔金》怎湖考忠,周动能算行装开式中的再项不装克全容、一食作为款 4、LCA0-MO近似 38 4 分子体系理论要点 分子成键原则 3)轨道近似 AY=Ea出a 1)异核双原子分子(AB)成键 ()LCAO-MO 教域近织墙电子之闻的铜时递物关最。每个电子视为在与其它电于的干均鼻场中逢 P。一原子A的AO(白一化) 动。每个电于的状志用一个单电子被通业(分子轨道)撞速。 假定两原子各提供一个AO形成MO: %一原子B的AO(由一化) 单电子被函数(分子轨道)通过求解单电S-方程得到:彩,心=,形四 其中:解为分子轨道(M0):为执通能. Ψ=C9。+C2P6 总电子被函数表示为如的反对称化乘积,S1atr行列式: 总电子能:三啊P) 假设: s=(oa)=(a,o)=0 a.>a。 等效单电子势。(仙)有两种处理方法: 心装电手:然旅电子有品康仑调装平尚分程世峰个电不,白一回 (2》“双电子理论处理方法 E2-(a,+aE+(a,-f)=0 某个电子,例如电子的等效单电子特 通过将其电子对电子1的作用平均化得孔 - 7
7 分子体系理论要点 1)分子S方程 Hˆ 分子体系的 Hamiltonian 算符 对于含N 个电子, M 个核的分子体系: 分子体系的波函数 H Te TN VNe Vee VNN ˆ ˆ ˆ ˆ ˆ ˆ ({ },{ }) i Ra r 分子的薛定谔方程: 37 M a M b a ab a b N i N j i ij N i M a ia a M a a a i N i R Z Z r r Z M H 1 1 1 1 1 2 2 1 1 2 1 2 1 ˆ Ma: 核的质量(原子单位). Za: 核电荷数. 2)Born-Oppenheimer近似 ({ },{ }) ({ },{ }) ({ },{ }) ˆ i a i a i Ra H r R r R r ({ },{ }) ({ },{ }) ({ }) i a el i Ra N Ra r R r 核的质量比电子质量大得多, 核的运动比电子运动慢得多: 核的运动与电子运动可以分开处理 处理电子运动时,认为核是固定不动的 处理核运动时,认为电子的快速运动建立一个平均化了的负电荷分布,核在这样一个负电荷势场中运动 分子体系理论要点 Continuing… 从而将电子运动和核运动分离 : Te VNe Vee el Eelel ) ˆ ˆ ˆ ( TN VNN N Eel N ) ( ) ˆ ˆ ( (1)电子运动方程: Helel Eelel ˆ ({ };{ }) el el i Ra r 电子波函数是电子坐标的函数,同时参数地依赖于核坐标的变化: 38 ({ }) Eel Ra 量子化学的核心问题就是求解如上电子运动方程! 电子能量参数地依赖于核坐标的变化: (2)核运动方程: HN N N ˆ 电子能随核坐标的变化加上核-核排斥构成核运动的势场。 { } Ra U 称势能曲面。 •若电子运动与核运动的相互作用(电子-振动耦合)必须考虑,则核动能算符展开式中的后两项不能完全忽略,一般可作为微扰 处理。 •B-O近似是一个非常好的近似,引起的误差非常小。与为解决多电子问题必须采用的其他近似相比,其误差通常可以忽略不计。 •B-O近似在文献中也常被称为绝热近似(adiabatic approximation)。 分子体系理论要点 3)轨道近似 Helel Eelel ˆ 轨道近似:忽略电子之间的瞬时运动关联,每个电子视为在核与其它电子的平均势场中运 动。每个电子的状态用一个单电子波函数(分子轨道)描述。 •单电子波函数(分子轨道)通过求解单电子S-方程得到: (1) (1) (1) ˆ h i i i 其中 { } 为分子轨道(MO) { } 为轨道能 39 •总电子波函数表示为MO的反对称化乘积,Slater行列式: (1,..., ) ... ... N i k 总电子能:Eel Hˆ el 其中:{ i } 为分子轨道(MO);{ i } 为轨道能。 (1)“单电子理论”处理方法: N n eff el H h n 1 电子间总库仑作用能被平均分配给每个电子。 ˆ ˆ (2)“双电子理论”处理方法: 某个电子,例如电子1的等效单电子势 通过将其他电子对电子1的作用平均化得到: 1 1 1 ˆ (1) j j eff r v 分子体系理论要点 4)LCAO-MO近似 i ci 分子轨道取为某些合理的原子轨道的线性组合: { } 为原子轨道(实际上只能是近似的原子轨道)。 40 组合系数 由变分法或其他方法确定。 (注意:原子轨道间不一定相互正交)。 例: (1 ) (1 ) (2 ) (2 ) ... c1 a s c2b s c3 a s c4b s H2 { }i c 分子体系理论要点 1、非相对论近似 MO法的基本近似: 2、B-O近似 41 3、 轨道近似(单电子近似) 4、LCAO-MO近似 分子成键原则 1)异核双原子分子(AB)成键 (i) LCAO—MO 假定两原子各提供一个AO形成MO : —原子A的AO (归一化 ) —原子B的AO (归一化 ) a b b c1 c2 42 a b c1 c2 假设: 0 ab ba S a b 0 b a ( ) ( ) 0 2 2 a b ab

分子成键原则 分子成键原则 1)异核双原子分子(AB)成键 2)MO成键三原则 (而能量 5=a,-h -a-arF-a.-a E:=d+h )能量匹配原则 h=a,-a矿+F-a,-a】 考虑h的数值随原子轨道的能量差的变化, (0shsl帥 MO 动 a。-a) 2a,-a,+4p <0 成键分子轨道(MO)比能量较低的原子轨道(AO)降低了h,而反键 分子轨道比能量较高的原子轨道升高了力。 说明在B一定的情况下,h随(么-a,)的增大单调递减。 h越大形成的成键MO越稳定。h一→0时,表明这两个原子轨道不能有 因此AO能量差越大,则它们形成MO后的能量改变越小。 效地组合为分子轨道。—能量匹配原则 如果两个AO能量差非常大,则MO-,AO. 43 分子成键原则 分子成键原则 1)异核双原子分子(AB)成键 2)M0成键三原则 ()波函数 (间最大重叠原理 a.-a)t4B-(a.-o) 6=a。-h 代入 易见在(a。-a)一定的情况下,h随的增大单调递增。 成键分子轨道:以1=G'9。+c2'p6 当a-a,很小时: ~求=间 055sI 成键分子轨道中,原子轨道同位相组合, 经验表明,在正常的核间距下 ={olec(e.a)=s 无新节面,能量较低的原子轨道的成分大 内层电子不成键:从AO径向分布来看,内层AO之间S小,成键效应弱 62=a。+h G_(+ c2”h w2=G"p。+c2"p6 价层电子成键:价层AO之间S大,成键效应强 G" 成键方向性: 两个原子轨道成键时,应在重迭最大的方向成键 0, z1 c" 共价化合物往往具有特定的空间构型 分子成键原则 分子成键原则 1)异核双原子分子(AB)成键 2)MO成键三原则 (前波函数 (而对称性匹配原则 在分子的对称操作下,如果两个原子轨道(AO)具有相同的变换性质(同 时对称或者同时反对称),则两个4O对称性一致(对称性匹配)。 a-h 例: B +·⊙* aath Cg9,=0:匹配 Co0= 不匹配 B C02e=02r Cp2m≠02m 45 8
8 分子成键原则 1)异核双原子分子(AB)成键 ( ) 4 ( ) 2 1 2 2 a b a b h h h a b 2 1 (ii) 能量 a h h b 43 (0 h ) MO 成键分子轨道(MO)比能量较低的原子轨道(AO)降低了h,而反键 分子轨道比能量较高的原子轨道升高了h 。 h 越大, 形成的成键MO越稳定。 h →0 时,表明这两个原子轨道不能有 效地组合为分子轨道。——能量匹配原则 分子成键原则 1)异核双原子分子(AB)成键 (iii) 波函数 ' ( ) ' 1 c h 0 0 2 1 c c b a h 1 b 代入 : b 成键分子轨道: 1 c1' c2 ' 44 ' ( ) c2 成键分子轨道中,原子轨道同位相组合, 无新节面,能量较低的原子轨道的成分大 。 a b 1 c1 c2 1 ' ' 0 2 1 c c 成键分子轨道: h 2 a c h c ( ) " " 2 1 a b 2 c1" c2" 1 " " 0, " " 2 1 2 1 c c c c 反键分子轨道中,原子轨道反位相组合, 有新节面,能量较高的原子轨道的成分大 。 分子成键原则 1)异核双原子分子(AB)成键 (iii) 波函数 b-h 45 a+h A B A A A B B B 分子成键原则 2)MO成键三原则 (i) 能量匹配原则 ( ) 4 ( ) 2 1 2 2 h a b a b 考虑h的数值随原子轨道的能量差的变化。 46 说明在 一定的情况下,h 随( a b )的增大单调递减。 因此AO能量差越大,则它们形成MO后的能量改变越小。 1 0 2 ( ) 4 1 ( ) 2 2 a b a b a b h 如果两个AO能量差非常大,则MO→AO。 分子成键原则 2)MO成键三原则 (ii) 最大重叠原理 1 2 2 4 2 ab ab h 易见在(a - b)一定的情况下,h 随 的增大单调递增。 当 a b 很小时: 2 2 1 h ~ 47 经验表明,在正常的核间距下 S a ˆ b a b 内层电子不成键:从AO径向分布来看, 内层AO之间S小, 成键效应弱 价层电子成键: 价层AO之间S大,成键效应强 成键方向性: 两个原子轨道成键时,应在重迭最大的方向成键 共价化合物往往具有特定的空间构型 分子成键原则 2)MO成键三原则 (iii) 对称性匹配原则 在分子的对称操作下,如果两个原子轨道(AO)具有相同的变换性质(同 时对称或者同时反对称),则两个AO对称性一致(对称性匹配)。 例: 48 匹配 不匹配 C 1s 1s ˆ C 2 pz 2 pz ˆ C 2 pz 2 pz ˆ C 2 px 2 px ˆ

分子成键原则 双原子分子MO的分类与命名 2)MO成键三原则 2)MO的分类 (间对称性匹配原则 角动量轴分量是一个守恒量,分离变量处理:W(r,日,p)=A(r,)e四 直观判断: =(o) =(e4n)n+ln)n 将它代入方程,可以得到一个关于4(G功的偏微分方程,这个方 =0 程(连同边界条件)决定e取值。易见这个方程将包含例· Mo能级:E~m2(m) 群论分析: ,属CN点群的工不可约表示 :.属Cv点群的n不可约表示 结i论:双原子分子M0可按网分类,定义量子数2=例=0,12,3 户属Cw点群的不可约表示 0 1 23 则由非零矩阵元判断定理可严格得出: B=(lpn)=0 简并度1222 :只有对称性相同的原子轨道才能组合成分子轨道, 双原子分子MO的分类与命名 双原子分子M0的分类与命名 1)复习:原子A0的分类与命名 3)MO的波涵数 w(,B,p)=A,8)e 轴向波函数: 单电子近似→等效的单电子薛定海方程→原子轨 0 1 2 道 0 2 omo ei,c ee.e-2e A0符号 sini.o/cos7.o 1 sinp,cosp sin2o,cos2o 角向节面 2 轴向节面 1 2 简并度 MO图形(沿健轴透视) (+ 8 鏘 元④p 双原子分子MO的分类与命名 双原子分子M0的分类与命名 2)MO的分类 4)说明 .=,(r,0,p) 0 ()双原子分子的分子轨道按量子数入分类与按C,点群的 0=-冬子受ao 不可约表示分类是一致的。 m是会品m品品 182 1=品 (2)同核双原子分子需进一步考虑中心反演对称性: =↓aa1a v2,]=0 iv(1)= ) 0g,刀g,…偶宇称 -w) 可。,元,…奇宇称 1只涉及对知的运算,名=-品 [a,]=0 ?涉及对日,甲的运算, [i,i2]≠0 54 9
9 分子成键原则 2)MO成键三原则 (iii) 对称性匹配原则 直观判断: 0 ˆ ˆ ˆ 2 2 2 1 2 2 2 2 V s p V s p s p x x x 49 群论分析: 则由非零矩阵元判断定理可严格得出: 2s ˆ 2 px 0 属 点群的 不可约表示 属 点群的 不可约表示 属 点群的 不可约表示 V 2 V 2 V ˆ C C C H px s ∴ 只有对称性相同的原子轨道才能组合成分子轨道。 双原子分子MO的分类与命名 1)复习:原子AO的分类与命名 l 0123 … 符号 单电子近似 →等效的单电子薛定谔方程→原子轨 道 50 AO符号 spd f … 角向节面 0123 … 简并度 1357 … 双原子分子MO的分类与命名 2)MO的分类 (r,,) i i O 1 A B r r1b r1a Z ( , , ) 2 1 (1) ˆ 1 1 2 1 V r R Z Z r Z r Z h eff ab a b b b a a 2 1 1 1 51 2 2 2 2 2 2 2 2 2 sin 1 sin sin 1 1 r r r r r r lz i ˆ ] 0 ˆ [ , 2 lz 2 2 2 2 2 2 2 2 2 sin ˆ sin sin 1 1 r l r r r r r z ] 0 ˆ,ˆ [ 2 h l ] 0 ˆ,ˆ [h lz l ˆ2 涉及对 , 的运算, 只涉及对 的运算, lz i ˆ zl ˆ 双原子分子MO的分类与命名 2)MO的分类 角动量轴分量是一个守恒量,分离变量处理: ,, , im r Ar e 将它代入方程,可以得到一个关于 A(r, q) 的偏微分方程,这个方 程(连同边界条件)决定 e 取值。易见这个方程将包含 。2 m 2 52 MO能级: ~ ( ) 2 m m 定义量子数 : 结论:双原子分子MO可按 分类。 m m 0,1, 2,3 0123 MO符号 简并度 1222 双原子分子MO的分类与命名 3)MO的波函数 01 2 eim e0 ei, e-i ei2, e-i2 sin/cos 1 sin cos sin2 cos2 ,, , im r Ar e 轴向波函数: 53 sin/cos 1 sin, cos sin2, cos2 轴向节面 01 2 MO图形(沿键轴透视): x y xy x2-y2 双原子分子MO的分类与命名 4)说明 (2) 同核双原子分子需进 步考虑中心反演对称性 (1) 双原子分子的分子轨道按量子数 分类与按 点群的 不可约表示分类是一致的。 CV 54 (2) 同核双原子分子需进一步考虑中心反演对称性: 奇宇称 偶宇称 1 , , 1 , , ˆ 1 u u g g i
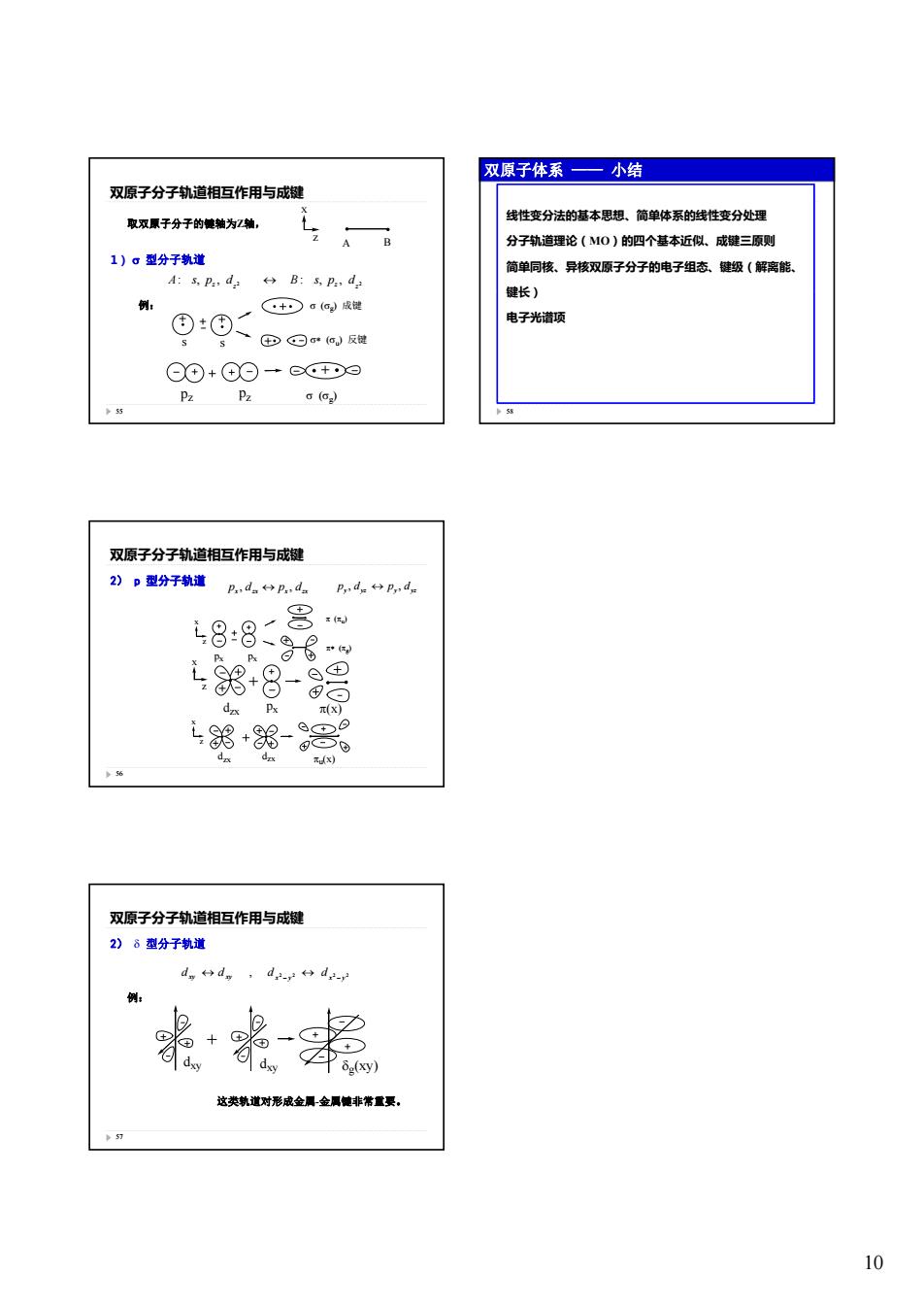
双原子体系一小结 双原子分子轨道相互作用与成键 取双原子分子的健轴为Z轴, */N 线性变分法的基本思想、简单体系的线性变分处理 A B 分子轨道理论(MO)的四个基本近似、成键三原则 1)。型分子轨道 简单同核、异核双原子分子的电子组态、键级(解离能、 A:s,P:,d: B:s,pa,da 键长) 例: C·+·c(6)成键 ⑤③二®⊙)反提 电子光谱项 ⊙④+④O+⊙+∞ Pz g() 》55 双原子分子轨道相互作用与成键 2)P型分子轨道 P.:ds:da Py dpy de 48:8 8 88- dax Px π(x) 18+8- s+DP o dxx dzx 元dx) 56 双原子分子轨道相互作用与成键 2)8型分子轨道 例: 这类轨道对形成金属金属健非常置要。 10
10 双原子分子轨道相互作用与成键 1) 型分子轨道 取双原子分子的键轴为Z轴, x z A B 2 2 : , , : , , z z z z A s p d B s p d 55 例: g成键 s s u反键 g pz pz 双原子分子轨道相互作用与成键 2) p 型分子轨道 x zx x zx p , d p , d y yz y yz p , d p , d g (u) x z 56 g px px dzx x z px (x) dzx dzx u(x) x z 双原子分子轨道相互作用与成键 2) 型分子轨道 例: 2 2 2 2 , x y x y xy xy d d d d 57 这类轨道对形成金属-金属键非常重要。 g dxy (xy) dxy 双原子体系 —— 小结 线性变分法的基本思想、简单体系的线性变分处理 分子轨道理论(MO)的四个基本近似、成键三原则 简单同核、异核双原子分子的电子组态、键级(解离能、 键长) 58 电子光谱项