
KeyyofMoDeparmentof Ch $9.1试验设计 试验方案的设计: 合理安排试验,分析试验结果和影响因素之间的关系, 确定影响因素的主次,从而寻找最佳的试验条件 试验设计必额考虑的问数 研究目的和方法 实验对象的选择及所需要的数量(抽样) 试验的分组设计和合理的选择 观察的指标和标准的方法 误差的来源和控制 要采用的掘取信息的方法 试验设计的目的就是为了试验优化: 振华制 2018/5/28 数理统计在化学中的应用
李 振 华 制 2018/5/28 数理统计在化学中的应用 1 造 $9.1 试验设计 试验方案的设计: 合理安排试验,分析试验结果和影响因素之间的关系, 确定影响因素的主次,从而寻找最佳的试验条件 试验设计必须考虑的问题 研究目的和方法 实验对象的选择及所需要的数量(抽样) 试验的分组设计和合理的选择 观察的指标和标准的方法 误差的来源和控制 要采用的掘取信息的方法 试验设计的目的就是为了试验优化

ihargtaiKgyLaboratoyofMdlecarCassandlhmoraireMteria冰,Depat恤etofCherity 日本: 工程师共同语言的一部分。 据说在日本,一个工程师如果没有试验设计这方面的知 识,就只能算半个工程师。此话乃出自一个华裔学者、 著名的工业工程专家吴玉印教授之口 中国: 试验设计的现代发展—稳健设计以及各种回归设计方 法的实际应用于20世纪70年代末、80年代初在我国才刚 刚开始。 仅正交试验设计的应用成果目前已超过10万项,经济效 益在50亿元以上。 还有较大的差距。 李振华制 2018/5/28 数理统计在化学中的应用
李 振 华 制 2018/5/28 数理统计在化学中的应用 2 造 日本: 工程师共同语言的一部分。 据说在日本,一个工程师如果没有试验设计这方面的知 识,就只能算半个工程师。此话乃出自一个华裔学者、 著名的工业工程专家吴玉印教授之口 中国: 试验设计的现代发展——稳健设计以及各种回归设计方 法的实际应用于20世纪70年代末、80年代初在我国才刚 刚开始。 仅正交试验设计的应用成果目前已超过10万项,经济效 益在50亿元以上。 还有较大的差距
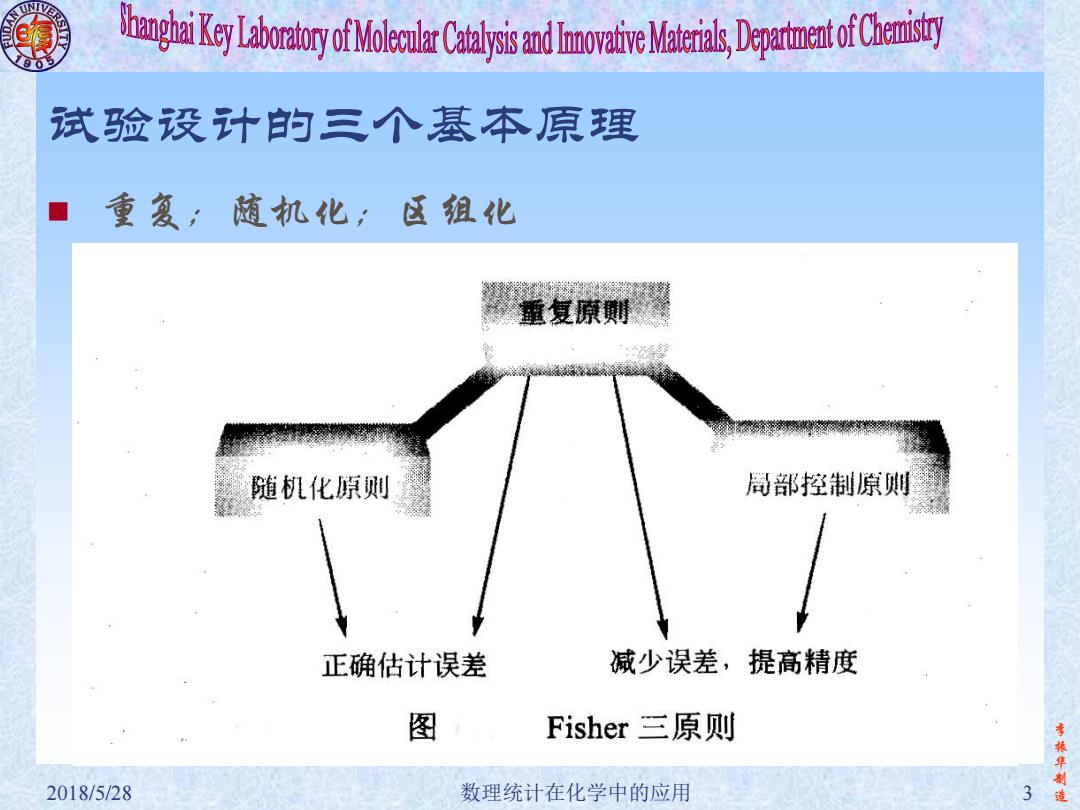
Key ryofMoDeparmentof Ch 试验设计的三个基本原理 重复;随机化:区组化 随机化原则 局部控制原则 正确估计误差 减少误差,提高精度 图 Fisher三原则 李振华制 2018/5/28 数理统计在化学中的应用 3
李 振 华 制 2018/5/28 数理统计在化学中的应用 3 造 试验设计的三个基本原理 重复;随机化;区组化

ihangthiKeyLhortnry0dfMolealarCasandhmowatreMateril,Deoat恤etofChsmity §9.1.1分组试验设计 1.完全随机设计分组 ■将各试验单位随机分配到各试验组 例8-6:动物试验分组之一 2.配对试验设计分组 将各试验对象先配对,再随机分组,如先按性 别,年龄,体重等相近的组成若干对 例8-7:动物试验分组之二 李 华制 2018/5/28 数理统计在化学中的应用
李 振 华 制 2018/5/28 数理统计在化学中的应用 4 造 §9.1.1 分组试验设计 1. 完全随机设计分组 将各试验单位随机分配到各试验组 例8-6:动物试验分组之一 2. 配对试验设计分组 将各试验对象先配对,再随机分组,如先按性 别,年龄,体重等相近的组成若干对 例8-7:动物试验分组之二

KeyofMoDeparmentof Ch 2.配对实验设计分组 有时候我们需要将试验对象先配对后,再随机分组,例如进行药物临床试验, 对病人就应按性别、年龄、体重等相近的的组成若干对,然后才能进行随机分组。 下面看一个例子。 「例8-71 动物试验分组之二 分组号 2 3 4 6 7 8 9 随机数字 23 71 08 0738 93 772741 单双数 单 单 双 单 双 单 单 单 单 病人1号 甲 甲 乙 甲 甲 甲 甲 病人2号 乙 乙 甲 乙 甲 乙 乙 乙 李 华制 2018/5/28 数理统计在化学中的应用
李振华制 2018/5/28 数理统计在化学中的应用 5 造
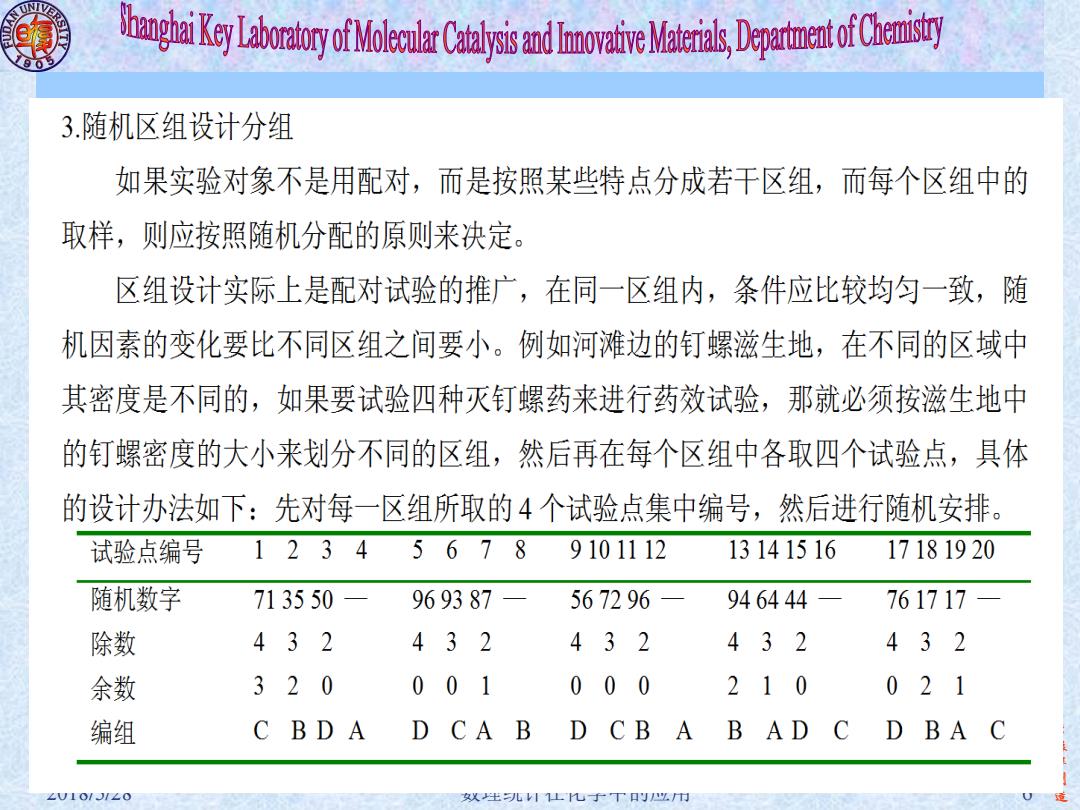
Key Loy of MDprmmtof C 3.随机区组设计分组 如果实验对象不是用配对,而是按照某些特点分成若干区组,而每个区组中的 取样,则应按照随机分配的原则来决定。 区组设计实际上是配对试验的推广,在同一区组内,条件应比较均匀一致,随 机因素的变化要比不同区组之间要小。例如河滩边的钉螺滋生地,在不同的区域中 其密度是不同的,如果要试验四种灭钉螺药来进行药效试验,那就必须按滋生地中 的钉螺密度的大小来划分不同的区组,然后再在每个区组中各取四个试验点,具体 的设计办法如下:先对每一区组所取的4个试验点集中编号,然后进行随机安排。 试验点编号 1234 5678 9101112 13141516 17181920 随机数字 713550 969387 567296 946444 761717 除数 432 432 432 432 432 余数 320 001 000 210 021 编组 C BDA D CA B D CB A B AD C D BA C 2U10/J1L0 双生儿LU子T则以中
李振华制 2018/5/28 数理统计在化学中的应用 6 造

KLao fMoaymovive Deparm of Ch §9.1.2简单比较和正交拉丁方 在分析试验设计中,当影响的因素较多时,就无法 对各个因素的每个水平进行全面的搭配实验,这就 需要寻找试验次数少而又能获得可靠结果的试验方 法。 通常,全面的因素试验只有在因素不多的情况下才 可能进行 6个因素+5个水平→56=15625 2018/5/28 数理统计在化学中的应用 李振华制造
李 振 华 制 2018/5/28 数理统计在化学中的应用 7 造 §9.1.2 简单比较和正交拉丁方 在分析试验设计中,当影响的因素较多时,就无法 对各个因素的每个水平进行全面的搭配实验,这就 需要寻找试验次数少而又能获得可靠结果的试验方 法。 通常,全面的因素试验只有在因素不多的情况下才 可能进行 6个因素+5个水平 5 6 =15625

KLaooy fMoayoiveDeprme of Ch 1.首单比较法 例如某合成反应,需要寻找最适宜的酸度(A)、试 荆浓度(B)、温度(C),每个因素分三个水平,一般 常用的简单做法是单因素条件试验,即首先人为地 园定A和B的量,来变化C。 C AL B2 C2 C2 C3 B: A3 李振华制 2018/5/28 数理统计在化学中的应用 8
李 振 华 制 2018/5/28 数理统计在化学中的应用 8 造 1.简单比较法 例如某合成反应,需要寻找最适宜的酸度(A)、试 剂浓度(B)、温度(C),每个因素分三个水平,一般 常用的简单做法是单因素条件试验,即首先人为地 固定A和B的量,来变化C。 C1 A1 B1 C2 C3 B1 A1 B2 C2 B3 A1 A2 B3 C2 A3

KLao fMoaaymovive Deparm of Ch 缺点: 1)看起来好象是做了9次试验,但实际上只是7次, 因为其中有两个各做了两次。 2)各因素,各水平出现的机会不等 3)C2是在AB1条件下最好,但其他条件下是香好, 志做试验,因此是不是最佳,并不确定。 4)当因素间交互作用影响比较大时,就不一定是各 种条件因素的最好的搭配组合。 5)用这种方法安排试验,如不重复做试验,是给不 出误差估计的,因此,同样的试验次数,提供信息 不多。 李振华制 2018/5/28 数理统计在化学中的应用
李 振 华 制 2018/5/28 数理统计在化学中的应用 9 造 缺点: 1)看起来好象是做了9次试验,但实际上只是7 次, 因为其中有两个各做了两次。 2)各因素,各水平出现的机会不等。 3)C2是在A1B1条件下最好,但其他条件下是否好, 未做试验,因此是不是最佳,并不确定。 4)当因素间交互作用影响比较大时,就不一定是各 种条件因素的最好的搭配组合。 5)用这种方法安排试验,如不重复做试验,是给不 出误差估计的,因此,同样的试验次数,提供信息 不多

ihanghaiKeyLabortryofMolsarCahsandhnowatireMateial,Depat恤eatofChiemity §9.1.3拉丁方狱验设计 怕衡分布思想,虽然远在古代就有,但只是在近代 才与生产科研实际相猪合,产生了拉丁方、正交表 ,显示出它的巨大威力。 18世纪的欧洲,普鲁士弗里德里希·威廉二世 1712一1786)要举行一次与往常不同的6列方队阅 兵式。他要求每个方队的行和列都要由6种部队的6 种军官组成,不得有重复和空缺。这样,在每个6 列方队中,部队军官在行和列全部排列均衡。群臣 们冥思苦想,竟无一人能郁出这种方队。后来,向 当时著名的数学家欧拉(1707一1783)清教,由此 引起了数学家们的极大兴趣,致使各种拉丁方问世 振华制 2018/5/28 数理统计在化学中的应用 10
李 振 华 制 2018/5/28 数理统计在化学中的应用 10 造 §9.1.3 拉丁方试验设计 均衡分布思想,虽然远在古代就有,但只是在近代 才与生产科研实际相结合,产生了拉丁方、正交表 ,显示出它的巨大威力。 18世纪的欧洲,普鲁士弗里德里希·威廉二世( 1712一1786)要举行一次与往常不同的6列方队阅 兵式。他要求每个方队的行和列都要由6种部队的6 种军官组成,不得有重复和空缺。这样.在每个6 列方队中,部队军官在行和列全部排列均衡。群臣 们冥思苦想,竟无一人能排出这种方队。后来,向 当时著名的数学家欧拉(1707—1783)请教,由此 引起了数学家们的极大兴趣,致使各种拉丁方问世