
第六章:HF与Post HF方法 Chapter 6 HF
第六章:HF与Post HF方法 1 Chapter 6 HF

6.1波西数与薛定号方程 1.波函数 德布罗意波→波函数平(化,t) 波函数是粒子状态的全部描述 体系的电子波函数 电子波函数 总电荷密度 差分电荷密度 >2 Chapter 6 HF
1. 波函数 2 Chapter 6 HF 6.1 波函数与薛定谔方程 德布罗意波 波函数 Ψ(x, t) 波函数是粒子状态的全部描述 电子波函数 总电荷密度 差分电荷密度 体系的电子波函数

6.1波函数与裤定污方程 2.Schrodinger Equation The Schrodinger equation second derivative in space a wave equation: first derivative in time p+v小=h 2 H 三 V2+V(可,t)= Hamiltonian 2m 节=-ih☑ +V=T+V 2m >3 Chapter 6 HF
2. Schrodinger Equation 3 Chapter 6 HF 6.1 波函数与薛定谔方程

6.1波函数与裤定污方程 3.N-particles problem 并非那么简单 Remember H妙=E吵 the good old days of the I-electron H-atom?? [- e2 ()=E() They're over! 22R-28 n e2 2M, R 2 R-R 2m i-1 kinetic energy of ions kinetic energy of electrons electron-ion interaction potential energy of ions electron-electron interaction Multi-Atom-Multi-Electron Schrodinger Equation H(R1,,Rw1,rn)Ψ(R1,,RN,,n)=EΨ(R1,,Rw1,n) Chapter 6 HF
3. N-particles problem 4 Chapter 6 HF 6.1 波函数与薛定谔方程 并非那么简单
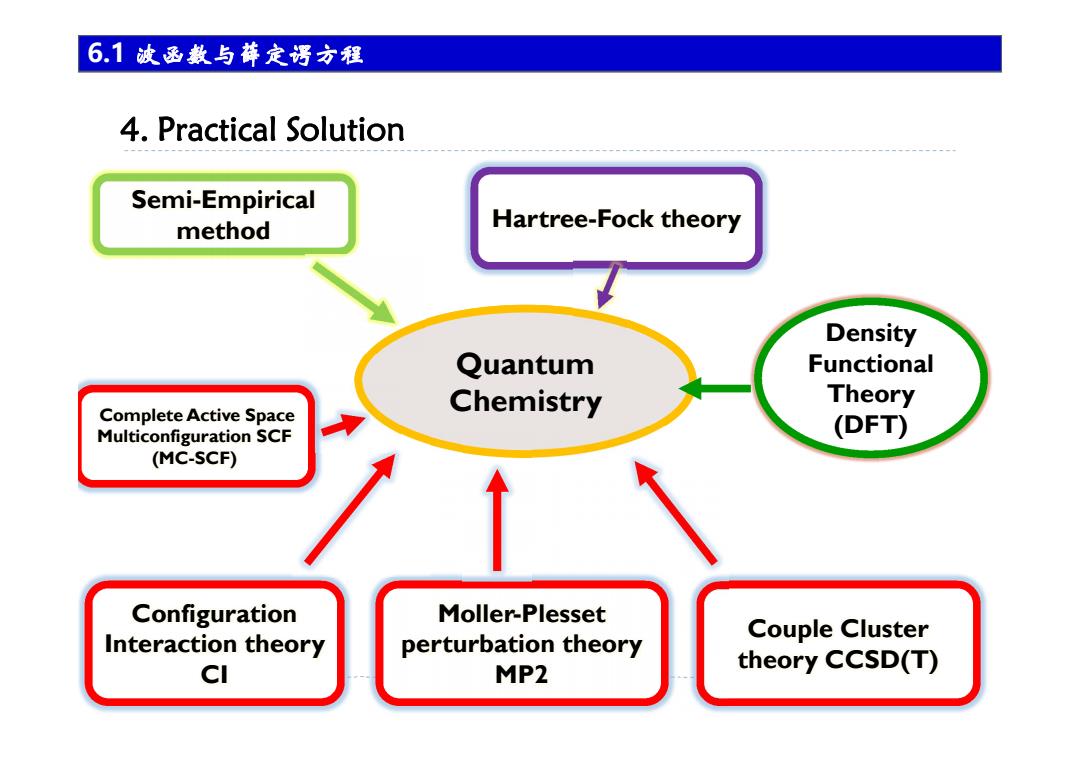
6.1波函数与裤定污方程 4.Practical Solution Semi-Empirical method Hartree-Fock theory Density Quantum Functional Theory Complete Active Space Chemistry Multiconfiguration SCF (DFT) (MC-SCF) Configuration Moller-Plesset Interaction theory Couple Cluster perturbation theory CI MP2 theory CCSD(T)
4. Practical Solution 5 Chapter 6 HF 6.1 波函数与薛定谔方程 Quantum Chemistry Density Functional Theory (DFT) Couple Cluster theory CCSD(T) Moller-Plesset perturbation theory MP2 Configuration Interaction theory CI Hartree-Fock theory Semi-Empirical method Complete Active Space Multiconfiguration SCF (MC-SCF)

6.1波函数与裤定号方程 5.关键近似 近似:非相对论近似 近似II:Bon-Oppenheimer绝热近似 近似川川:单电子近似(轨道近似) Interacting Non-Interacting 体系Hamilton量简化 单电子薛定谔方程 hi=P P,为单电子波函数or分子轨道(MO) 本征值6,为对应的分子能级 Chapter 6 HF
5. 关键近似 6 Chapter 6 HF 6.1 波函数与薛定谔方程 近似II:Born-Oppenheimer 绝热近似 近似I:非相对论近似 近似III:单电子近似(轨道近似) 体系Hamilton量简化 单电子薛定谔方程 or

6.1波函数与薛定号方程 5.总电子波函数 由于体系状态波函数采用不同形式的单电子波函数组 合,就产生不同的计算水平。 Wave-Based Methods) 简单的单电子乘积: Hartree方程 Slater行列式: Hartree-Fock方程 LCAO-MO方法: Hartree-Fock-Roothaan方程 多组态波函数: 组态相互作用 (Configuration Interaction,Cl) Chapter 6 HF
5. 总电子波函数 7 Chapter 6 HF 6.1 波函数与薛定谔方程 由于体系状态波函数采用不同形式的单电子波函数组 合,就产生不同的计算水平。 (Wave-Based Methods) 简单的单电子乘积: Hartree 方程 Slater行列式: Hartree-Fock方程 LCAO-MO方法: Hartree-Fock-Roothaan方程 多组态波函数: 组态相互作用 (Configuration Interaction, CI)

6.2 Hartree六程 无相互作用? Write wavefunction as a simple product of single particle states: Hartree积(HP多体波函数) Ψ(r1,…,rn)=p1(r1)p2(r2).pn(rn) Hard Product of Easy Total energy E=∑6 >8 Chapter 6 HF
无相互作用? 8 Chapter 6 HF 6.2 Hartree方程 Hartree 积 (HP多体波函数) Total energy

6.2 Hartree六程 Hartree方程 ·对HP多体波函数 = 2mi Hartree Approximation:the electrons do not interact explicitly with the others,but each P,=lofe electron interacts with the medium potential given by the other electrons 变分法 +2 where: =小o血0t,间吉:+兰子,鷓子盼 J=小Φ02tdt。 -库仑双电子积分 -代表经典两个电荷密度之间的排斥作用 由中:and中,描述) Chapter 6 HF
Hartree方程 9 Chapter 6 HF 6.2 Hartree方程 • 对HP多体波函数 Hartree Approximation: the electrons do not interact explicitly with the others, but each electron interacts with the medium potential given by the other electrons 变分法 = ≠ = = = + N i 1 N j i j 1 ij N i 1 E Hi J 21 = = − ∇ + − = i i MA 1 iA 2 A i i i i i i i Φ (i)dτ rZ 21 H Φ (i)h Φ (i)dτ Φ (i) where: - 单电子积分项 = 1 2 2j 12 2 ij i Φ (2)dτ dτ r1 J Φ (1) -库仑双电子积分 -代表经典两个电荷密度之间的排斥作用 (由 Φi and Φj 描述)

6.2 Hartree方程 自洽场计算(SCF) Using the Lagrange's multipliers method Hartree equations: -生么+空可血0=e间 2 A=1 e,=H+∑Jj ·分子轨道能量 总能量 E-2,-22 i=1 i=1j=i+1 >10 Chapter 6 HF
自洽场计算 (SCF) 10 Chapter 6 HF 6.2 Hartree方程 dτ Φ (i) ε Φ (i) r 1 Φ (j) r Z 2 1 i i i N i 1 N j i j 1 j ij 2 j M A 1 iA 2 A i = − ∇ +− + = ≠ = = Using the Lagrange’s multipliers method Hartree equations: ≠ = = + N j i j 1 i Hi Jij ε - 分子轨道能量 = = + = = − N-1 i 1 N j 1 ij N i 1 E i J i 总能量 ε