
第六章络合物结构和配位场理论.149 6.1络合物的价键理论..149 6.1.1价键理论 .149 6.1.2价键理论的成功和局限性 150 6.2晶体场理论. 150 6.2.1正八面体配位场的势能函数 .150 62.2在正八面体配位场中d轨道的能级分裂 151 6.2.3正四面体场中d轨道的能级分裂 .154 6.2.4高自旋态和低自旋态 6.2.5晶体场稳定化能(CSE). 156 6.2.6络合物的畸变和姜-泰勒(Jahn-Teller)效应 .157 6.3络合物的分子轨道理论 157 6.3.1配位体群轨道 157 6.3.2络合物的分子轨道 6.3.3络合物中的π键… 15g 习题. .160
1 第六章 络合物结构和配位场理论 ..................................................................................................................... 149 6.1 络合物的价键理论 .................................................................................................................................... 149 6.1.1 价键理论 ............................................................................................................................................. 149 6.1.2 价键理论的成功和局限性 ................................................................................................................. 150 6.2 晶体场理论 ................................................................................................................................................ 150 6.2.1 正八面体配位场的势能函数 ............................................................................................................. 150 6.2.2 在正八面体配位场中 d 轨道的能级分裂 .......................................................................................... 151 6.2.3 正四面体场中 d 轨道的能级分裂 ..................................................................................................... 154 6.2.4 高自旋态和低自旋态 ......................................................................................................................... 155 6.2.5 晶体场稳定化能(CFSE) ..................................................................................................................... 156 6.2.6 络合物的畸变和姜-泰勒(Jahn-Teller)效应 ........................................................................................ 157 6.3 络合物的分子轨道理论 ............................................................................................................................ 157 6.3.1 配位体群轨道 ..................................................................................................................................... 157 6.3.2 络合物的分子轨道 ............................................................................................................................. 159 6.3.3 络合物中的 π 键 ................................................................................................................................. 159 习题 ..................................................................................................................................................................... 160

第六章 络合物结构和配位场理论 由中央原子(或离子)和其周围的若干分子或离子所组成的化台物叫络合物,中央原子或离子称为络 合物的核,与核相结合的分子或离子称为配位体.根据络合物所含核的数量可以分为单核络合物和多核络 合物。带有电荷的结合物你为络离子,络合物的接通常是过渡金属原子或离子,配位体通常是含有孤对电 子或π键的分子或离子, 6.1络合物的价键理论 6.1.1价键理论 本世纪30年代,L.Pauling提出:络合物的中央离子(或原子)和配位体之间的化学键可分为电价配键 和共价配键两种,相应的络合物称为电价络合物和共价络合物.在电价络合物中,带正电的中央离子和带 负电或具有偶极矩的配位体之间是靠静电引力结合成键,这种静电引力不会影响中央离子的电子结构,故 中央离子的电子排布将按Hud规则,即电子尽可能分占不同的轨道而且自旋相互平行,这样电价络合物往 往含有较多的自旋平行电子,而呈高自旋状态,一般来说,当中央原子和配位体原子的电负性相差较大时, 则容易形成电价结合物.故含氟、氧等原子的配位体(如F,H0等)常与金属离子生成电价结合 物.[FeF6J3,Fe(H2O)6J3t,NiNH)6+,[CoNH)6J2+,Mn(NH)62+等都是电价络合物. 在共价络合物中,配位体的孤对电子和中央离子空的杂化价轨道形成共价σ配键.在这些杂化轨道中 以sp2,dsp,p,sp,p2和p杂化为常见,相应络合物的几何构型分别为正八面体、平面正方形、正 十二面体、正四面体、正三角形和直线形.为了腾出空d轨道参与杂化,d电子常被挤到少数d轨道中而成 自旋相互反平行的自旋配对状态,这样,自旋平行的电子则较少,故共价络合物一般为低自旋络合物.有 时少数d电子还要激发到较高能级的空轨道上去,以腾出足够多的空d轨道参与杂化,其升高的激发能量 将被较多的成键面带来的较多的能量下降所补偿.Fe3#的电子结构是3d4s°4p°,即 4s 个个个个个 3d 当它与六个CN配位体形成F(CN63络离子时,Fe3#的5个d电子被挤到三个d轨道中,空出两个d轨道 和4s,4p轨道形成d2sp杂化轨道.这六个指向正八面体顶点的杂化轨道容纳六个CN-配位体上的孤对电 子,形成六个共价配键,这可表示为 ↓个二= 3d dsp 由于这六个共价配键的形成,使分子体系的能量显著降低而稳定, 149
149 第六章 络合物结构和配位场理论 由中央原子(或离子)和其周围的若干分子或离子所组成的化台物叫络合物,中央原子或离子称为络 合物的核,与核相结合的分子或离子称为配位体.根据络合物所含核的数量可以分为单核络合物和多核络 合物.带有电荷的结合物你为络离子,络合物的接通常是过渡金属原子或离子,配位体通常是含有孤对电 子或 π 键的分子或离子. 6.1 络合物的价键理论 6.1.1 价键理论 本世纪 30 年代,L.Pauling 提出:络合物的中央离子(或原子)和配位体之间的化学键可分为电价配键 和共价配键两种,相应的络合物称为电价络合物和共价络合物.在电价络合物中,带正电的中央离子和带 负电或具有偶极矩的配位体之间是靠静电引力结合成键,这种静电引力不会影响中央离子的电子结构,故 中央离子的电子排布将按 Hund 规则,即电子尽可能分占不同的轨道而且自旋相互平行,这样电价络合物往 往含有较多的自旋平行电子,而呈高自旋状态,一般来说,当中央原子和配位体原子的电负性相差较大时, 则容易形成电价结合物.故含氟、氧等原子的配位体(如 F- ,H2O 等)常与金属离子生成电价结合 物.[FeF6] 3-,[Fe(H2O)6] 3+,[Ni(NH3)6] 2+,[Co(NH3)6] 2+,[Mn(NH3)6] 2+等都是电价络合物. 在共价络合物中,配位体的孤对电子和中央离子空的杂化价轨道形成共价 σ 配键.在这些杂化轨道中 以 d2 sp 2 ,dsp 2 ,d4 sp 3 ,sp 3 ,sp 2和 sp 杂化为常见,相应络合物的几何构型分别为正八面体、平面正方形、正 十二面体、正四面体、正三角形和直线形.为了腾出空 d 轨道参与杂化,d 电子常被挤到少数 d 轨道中而成 自旋相互反平行的自旋配对状态,这样,自旋平行的电子则较少,故共价络合物一般为低自旋络合物.有 时少数 d 电子还要激发到较高能级的空轨道上去,以腾出足够多的空 d 轨道参与杂化,其升高的激发能量 将被较多的成键面带来的较多的能量下降所补偿.Fe3+的电子结构是 3d 5 4s 0 4p 0 ,即 4p 4s 3d 当它与六个 配位体形成[Fe(CN)6] 3-络离子时,Fe3+的 5 个 d 电子被挤到三个 d 轨道中,空出两个 d 轨道 和 4s,4p 轨道形成 d 2 sp 3 杂化轨道.这六个指向正八面体顶点的杂化轨道容纳六个 CN-配位体上的孤对电 子,形成六个共价配键,这可表示为 3d d2 sp3 由于这六个共价配键的形成,使分子体系的能量显著降低而稳定. CN-

Co2+含有七个d电子,当六个d电子挤到三个d轨道中之后,为了采用dsp杂化,则需要将一个d电 子激发到能量较高的5s轨道上去,因此[Co(CN)6很容易失去一个电子而变成[Co(CN)6,所以[Co(CN)6 是一个很强的还原剂,它能把水中的H还原成H2,自己则变成三价钴络离子[Co(CN)63 含有P结构的N2+,Pd2+,PP+和Au3+等离子在形成络合物中需要4个d轨道容纳8个d电子,所以只 能以一个空d轨道和s,p轨道杂化形成dsp2杂化轨道,它接受配位体的孤对电子而形成平面正方形络合物, [Ni(CN)4,[Pt(NH3)4,[Pt(CN)4,[PtCI],[Pt(NH3)2C12],[PdClP,[Pd(CN)4P,[Pd(NH)[AuCI] 等都是具有dsp杂化的平面正方形络合物.在这类络合物中,中心离子空的p轨道还可与配位体的π轨道 重迭而形成离域键. 含有d电子结构中心离子的络合物如[CuNH)62+,[CuCl2,[Cu(CN)42等,中央离子将一个d电子 激发到4p轨道上去,采用dsp2杂化,故也是平面正方形构型.在[Cu(CN)6中,未参加杂化的4p轨道还 可以和CN中的π轨道作用形成离域π键Ⅱ,’,这就增加了络合物的稳定性. 含有d0电子结构的[Ag(CN)2J和[ZnCL,2分别果用sp和sp杂化而成直线型和正四面体的络合物. 6.1.2价键理论的成功和局限性 络合物的价键理论说明了高自旋络合物和低自旋络合物产生的原因,对络合物的磁性和几何构型也都 给予了一定的说明.但价键理论截然将络合物划分为电价和共价两类,并把高自旋络合物看成是电价的, 低自旋络合物看成是共价的,这种方法有时和实验事实并不完全符合,例如三价铁的乙酰丙酮络合物 [F©(CHO2],实验测得有五个未配对电子,应属高自旋的电价络合物一类,但它易挥发、易溶于非极性 有机溶剂的性质却是共价化合物的特性,价键理论还无法解释络合物的颜色,络合物的稳定性随中央离子d 电子数变化而变化的现象,以及有些络合物几何构型会发生变形等现象。 6.2晶体场理论 为解释络合物的一系列性质,在络合物的价键理论之后,贝特(H.Bethe)和范夫利克(J.H.Van Vleck) 于1932~1935年提出了晶体场理论(C℉T).晶体场理论把配位体和中央离子的静电作用看成是各配位体叫 点电荷形式同中央离子的作用,使得中央离子能量简并的d轨道发生分裂. 6.2.1正八面体配位场的势能函数 设络合物中心离子位于直角坐标系的原点,六个配位体位于x,y,:轴上和中心离子等距离的六个顶点 上,其几何构型为正八面体,如图6.1所示.每个配位体L与原点的距离为α,它在空间某点Q(x,y,)处产生 的势场为V,计算出各配位体的,再把六个配位体的V,相加便可得到所有配位体在Qx,八,)点的势场. 设点电荷L1且在相距为R的Q处产生的静电势为,则 g (6-1) R L 其中-g为配位体L1的负电荷.由于 R=(a2+r2-2arcos0)R (6-2) 式中r为Qx,y,)点的矢径,a为r和z轴的夹角,如图6.2所示,忽略中 心离子在半径为a的球外部分的影响,即只考虑r<a的区域,并由Legendre L3 多项式的母函数的定义,有 1 1 y 1 1 =2P(10g(6-3) 图6.1正八面体场坐标 R va2[1+(r/a)2-2(r/a)cos0 a (1-2gt+g2)1/2 a 150
150 Co2+含有七个 d 电子,当六个 d 电子挤到三个 d 轨道中之后,为了采用 d 2 sp 5 杂化,则需要将一个 d 电 子激发到能量较高的 5s 轨道上去,因此[Co(CN)6] 4-很容易失去一个电子而变成[Co(CN)6] 3-,所以[Co(CN)6] 4- 是一个很强的还原剂,它能把水中的 H+ 还原成 H2,自己则变成三价钴络离子[Co(CN)6] 3-. 含有 d8 结构的 Ni2+,Pd2+,Pt2+和 Au3+等离子在形成络合物中需要 4 个 d 轨道容纳 8 个 d 电子,所以只 能以一个空 d 轨道和 s,p 轨道杂化形成 dsp2 杂化轨道,它接受配位体的孤对电子而形成平面正方形络合物, 如[Ni(CN)4] 2-,[Pt(NH3)4] 2+,[Pt(CN)4] 2-,[PtCl4] 2-, [Pt(NH3)2Cl2],[PdCl4] 2-,[Pd(CN)4] 2-,[Pd(NH3)6] 2+和[AuCl4] - 等都是具有 dsp2 杂化的平面正方形络合物.在这类络合物中,中心离子空的 p 轨道还可与配位体的 π 轨道 重迭而形成离域键. 含有 d9 电子结构中心离子的络合物如[Cu(NH3)6] 2+,[CuCl4] 2-,[Cu(CN)4] 2-等,中央离子将一个 d 电子 激发到 4p 轨道上去,采用 dsp2 杂化,故也是平面正方形构型.在[Cu(CN)6] 2-中,未参加杂化的 4p 轨道还 可以和 CN- 中的 π 轨道作用形成离域 π 键 Π9 9 ,这就增加了络合物的稳定性. 含有 d10电子结构的[Ag(CN)2] - 和[ZnCl4] 2-分别果用 sp 和 sp 3 杂化而成直线型和正四面体的络合物. 6.1.2 价键理论的成功和局限性 络合物的价键理论说明了高自旋络合物和低自旋络合物产生的原因,对络合物的磁性和几何构型也都 给予了一定的说明.但价键理论截然将络合物划分为电价和共价两类,并把高自旋络合物看成是电价的, 低自旋络合物看成是共价的,这种方法有时和实验事实并不完全符合,例如三价铁的乙酰丙酮络合物 [Fe(C5H7O2)3] 3+,实验测得有五个未配对电子,应属高自旋的电价络合物一类,但它易挥发、易溶于非极性 有机溶剂的性质却是共价化合物的特性,价键理论还无法解释络合物的颜色,络合物的稳定性随中央离子 d 电子数变化而变化的现象,以及有些络合物几何构型会发生变形等现象. 6.2 晶体场理论 为解释络合物的一系列性质,在络合物的价键理论之后,贝特(H.Bethe)和范夫利克(J.H. Van Vleck) 于 1932~1935 年提出了晶体场理论(CFT).晶体场理论把配位体和中央离子的静电作用看成是各配位体叫 点电荷形式同中央离子的作用,使得中央离子能量简并的 d 轨道发生分裂. 6.2.1 正八面体配位场的势能函数 设络合物中心离子位于直角坐标系的原点,六个配位体位于 x,y,z 轴上和中心离子等距离的六个顶点 上,其几何构型为正八面体,如图 6.1 所示.每个配位体 L 与原点的距离为 a,它在空间某点 Q(x, y, z)处产生 的势场为 Vi,计算出各配位体的 Vi,再把六个配位体的 Vi相加便可得到所有配位体在 Q(x, y, z)点的势场. 设点电荷 L1 且在相距为 R 的 Q 处产生的静电势为 V1,则 V1= ି ோ (6-1) 其中െq 为配位体 L1 的负电荷.由于 R=(a 2 +r 2 െ2arcosθ) 1/2 (6-2) 式中 r 为 Q(x,y,z)点的矢径,a 为 r 和 z 轴的夹角,如图 6.2 所示,忽略中 心离子在半径为 a 的球外部分的影响,即只考虑 r<a 的区域,并由 Legendre 多项式的母函数的定义,有 ଵ ோ = ଵ ඥమሾଵାሺ ⁄ ሻమିଶሺ ⁄ ሻୡ୭ୱఏ= ଵ ଵ ሺଵିଶ௧ାమሻభ మ⁄ = ଵ t l Pl(t)g l (6-3) 图 6.1 正八面体场坐标 x y z L1 L2 L3 L4 L6 L5

1 d 其中,g=rla,=cos0 P02项c0-y (6-4) P(t)是I次的Legendre多项式.将(6-3)和(6-4)代入(6-1)得 VPcos0) (6-5) a i=0 a 前几个Pcos)为 1 Po(cos0)=1 P(cose)=cos0 P:(cos0)-(3cos0-1) P(cos0)-(5cos0-3cos0) P.(cos0)(35cos0-30cos@+3)(6-6) 可以证明高于五次的项如Ps(cos0),P6(cos)等对d电子在配位场中能量 图62正八面体络合物的极坐标 计算中的贡献为零,所以可以取 h=-l+Pucos0H日p,(cos0H日Pcos0+FP,(cos0 1(6-7) L2位于z轴上(0,0,-a)处,计算3时只须将1中的cos换成cos(π-0)即可,注意到 cos"(π-0=(-1)”cos0 (6-8) 可得 -l-白Pcos00+日P(cos0-日Ps(cos0+fpa(cos0 (6-9) 故可得 +g-91HPcs0jr日p.cos0叭 (6-10) 注意到(6-6)式和 cos0=z/r (6-11) 有 +治紧-品 8ar42-3 (6-12) 从(6-12)式看出,位于z轴上的两个配证体L1和L2在Qx,y,)点产生的势能只和Q点到原点的距离 上,Q点在z轴上的投影,以及L1和L2到原点的距离a有关.据此可得 11L23x211435x430x2 V-a1+2a2-103 8ar42-3 (6-13) +V=- 1123y2 (6-14) 最后可得六个配位体点电荷在Q(x,y,)点的配位场势能函数为 含g器 (6-15) i=0 5 V中的第一项与Q点坐标无关,相当于配位体的-6g电荷均匀分布在以原点为球心,半径为α的球壳上对球 壳内部产生的电势,它对于中央离子来说是球对称的,它只会使中央离子的5个d轨道都提高到同一能量 水平,V中的第二项与配位体的空间排布有关,正是它,才使得简并的中央离子d轨道产生分裂. 6.2.2在正八面体配位场中d轨道的能级分裂 配位体相同的正八面体络合物属于O点群,因O群的最高不可约表示为三维,如果以中央离子的五 个d轨道为基底,所求得的是此点群的一个五维可约表示,它可以分解为若干不可约表示的和,逸就表明 了中央离子的d轨道在O,配位体场作用下的分裂.Oh的不可约表示分为偶表示(g)和奇表示()两种,它们 在中心反演操作下不改变和改变符号.以偶函数为基底的表示一定是偶表示,以奇函数为基底的表示一定 是奇表示,五个d轨道都是偶函数,所以以五个d轨道为基底的表示也一定为偶表示.于是只需用O群的 子群O群就可以确定d轨道的分裂情况. 151
151 其中,g= r/a,t=cosθ Pl(t)= ଵ ଶ! ୢ ୢ௧ (t 2 െ1)l (6-4) Pl(t)是 l 次的 Legendre 多项式.将(6-3)和(6-4)代入(6-1)得 V1= ି l 0 ( ) l Pl(cosθ) (6-5) 前几个 Pl(cosθ)为 P0(cosθ)=l P1(cosθ)=cosθ P2(cosθ)= ଵ ଶ (3cos2 θെ1) P3(cosθ)= ଵ ଶ (5cos3 θെ3cosθ) P4(cosθ)= ଵ ଼ (35cos4 θെ30cos2 θ+3) (6-6) 可以证明高于五次的项如 P5(cosθ),P6(cosθ)等对 d 电子在配位场中能量 计算中的贡献为零,所以可以取 V1=െ ݍ ܽ[1+( )P0(cosθ)+( ) 2 P2(cosθ)+( ) 3 P3(cosθ)+( ) 4 P4(cosθ)] (6-7) L2 位于 z 轴上(0, 0, െa)处,计算 V2 时只须将 V1 中的 cos 换成 cos(πെθ)即可,注意到 cosn (πെθ)=(െ1)n cosθ (6-8) 可得 V2=െ ݍ ܽ[1െ( )P0(cosθ)+ ( ) 2 P2(cosθ)െ( ) 3 P3(cosθ)+( ) 4 P4(cosθ)] (6-9) 故可得 V1+V2=െଶ [1+( ) 2 P2(cosθ)+( ) 4 P4(cosθ)] (6-10) 注意到(6-6)式和 cosθ=z/r (6-11) 有 V1+V2=െଶ [1+ ଵ ଶ ( ) 2 ( ଷ௭మ మ െ1)+ ଵ ଼ ( ) 4 ( ଷହ௭ర ర + ଷ௭మ మ െ3)] (6-12) 从(6-12)式看出,位于 z 轴上的两个配证体 L1 和 L2 在 Q(x,y,z)点产生的势能只和 Q 点到原点的距离 r, Q 点在 z 轴上的投影 z,以及 L1 和 L2到原点的距离 a 有关.据此可得 V3+V4=െଶ [1+ ଵ ଶ ( ) 2 ( ଷ௫మ మ െ1)+ ଵ ଼ ( ) 4 ( ଷହ௫ర ర + ଷ௫మ మ െ3)] (6-13) V3+V4=െଶ [1+ ଵ ଶ ( ) 2 ( ଷ௬మ మ െ1)+ ଵ ଼ ( ) 4 ( ଷହ௬ర ర + ଷ௬మ మ െ3)] (6-14) 最后可得六个配位体点电荷在 Q(x,y,z)点的配位场势能函数为 V1= 6 0 i Vi=െ െଷହ ସఱ(x 4 +y 4 +z 4 െଷ ହ r 4 ) (6-15) V 中的第一项与 Q 点坐标无关,相当于配位体的-6q 电荷均匀分布在以原点为球心,半径为 a 的球壳上对球 壳内部产生的电势,它对于中央离子来说是球对称的,它只会使中央离子的 5 个 d 轨道都提高到同一能量 水平,V 中的第二项与配位体的空间排布有关,正是它,才使得简并的中央离子 d 轨道产生分裂. 6.2.2 在正八面体配位场中 d 轨道的能级分裂 配位体相同的正八面体络合物属于 Oh 点群,因 Oh 群的最高不可约表示为三维,如果以中央离子的五 个 d 轨道为基底,所求得的是此点群的一个五维可约表示,它可以分解为若干不可约表示的和.逸就表明 了中央离子的 d 轨道在 Oh 配位体场作用下的分裂.Oh 的不可约表示分为偶表示(g)和奇表示(u)两种,它们 在中心反演操作下不改变和改变符号.以偶函数为基底的表示一定是偶表示,以奇函数为基底的表示一定 是奇表示,五个 d 轨道都是偶函数,所以以五个 d 轨道为基底的表示也一定为偶表示.于是只需用 Oh 群的 子群 O 群就可以确定 d 轨道的分裂情况. 图 6.2 正八面体络合物的极坐标 x y z a r L1 θ ϕ

O群的特征标表如表6-1所示 表6-1O群的特征标表 6C4 3C2 8C36C2 A 1 1 1 (6x2+y2+2) A2 -1 E 2 2 0 ) T 0 3 0 1 (xyJz,x) elmo 原子轨道也可以取 中a1m=Rakr)88√2元 (6-16) 同一壳层的五个d轨道其m分别为2,1,0,-1和-2,对应的d轨道记为d,d山,d6,d.1,和d2.它们和五 个实的d轨道间有下面的U,变换关系 r1 0 0 0 07 1 d22 0 2 0 0 do dxz 0 i 元 1 0 0 d, dyz d-1 (6-17) dx2-y2 0 0 0 1 dxy 2 d-2 0 0 1 ] 若将任意的转动轴选为原子轨道的z轴,则对绕此轴的转动而言,只有p角变化,径向函数Rnr)及9m(0 都保持不变.转动C(a)作用于中n1m上有 eim(p+a C(a)m(r,0,p)RAr)Oim(0 =ema中n1mr,0,p) 2π (6-18) 「ei2a 0 0 0 01f do d 0 eia 0 0 0 d 于是 C(a) d-1 0 0 1 0 0 d (6-19) d2 0 0 0 eia 0 ]L 0 000 e-i2alld_2 这个转动操作的特征标Xa)是X(a)=e2m+eia+e0a+eia+e2a=2cos2a+2cost1 (6-20) 当O群的纯转动操作E,C4,C2,C和C2作用于d轨道上时,其变换矩阵的特征标分别为 X(E)=5 x(C2)=X(C2)=1 x(C3)=-1 X(C4)=-1 利用点群的可约表示向不可约表示分解的公式a京RX(R 1 (6-21) 将以五个d轨道为基底的可约表示「分解为不可约表示 a41245×1+6×(-I)×1+3x1x1+8×(-1)x1+6×1×刘]=0 1 a42 245x1+6x(-1)x-IH3×1x1+8×(-1)x1+6x1x-10 aE245×2+6x(-1)x0+3x×2+8x(-1)x(-1)+6x1x0=l 1 an 245x3+6×(-l)x1+3xx(-1+8×(-)x0+6x1x-1片0 1 an245x3x6x(-l)x(-)+3×1×(-)+8x(-1)x0+6x1×1]=l 这可表示为 T=e+2 (6-22) 152
152 O 群的特征标表如表 6-1 所示 表 6-1 O 群的特征标表 O E 6C4 3C2 8C3 6ܥଶ ᇱ A1 A2 E T1 T2 1 1 2 3 3 1 െ1 0 1 െ1 1 1 2 െ1 െ1 1 1 െ1 0 0 1 െ1 0 െ1 1 (x 2 +y 2 +z 2 ) ൬ 2ݖଶ െ ݔଶ െ ݕଶ ݔଶ െ ݕଶ ൰ (xy,yz,xz) 原子轨道也可以取 ϕn l m=Rn l(r)Θlm(θ)( ୣക √ଶగ ) (6-16) 同一壳层的五个 d 轨道其 m 分别为 2,1,0,-1 和-2,对应的 d 轨道记为 d2,d1,d0,d-1,和 d-2.它们和五 个实的 d 轨道间有下面的 U,变换关系 ۏ ێ ێ ێ ێ ௭మ ݀ۍ ݀௫௭ ݀௬௭ ݀௫మି௬మ ے ௫௬݀ ۑ ۑ ۑ ۑ ې = ۏ ێ ێ ێ ێ ێ ێ ێ ۍ 10 0 0 0 0 1 ඥ2 1 ඥ2 0 0 0 െ i ඥ2 1 ඥ2 0 0 00 0 1 ඥ2 1 ඥ2 0 0 0െ 1 ඥ2 1 ےඥ2 ۑ ۑ ۑ ۑ ۑ ۑ ۑ ې ۏ ێ ێ ێ ۍ ݀ ݀ଵ ݀ିଵ ݀ଶ ےଶ݀ି ۑ ۑ ۑ ې (6-17) 若将任意的转动轴选为原子轨道的 z 轴,则对绕此轴的转动而言,只有 φ 角变化,径向函数 Rn l(r)及 Θl m(θ) 都保持不变.转动ܥመ(α)作用于 ϕn l m上有 ܥመ(α)ϕn l m(r, θ,φ)=Rn l(r)Θl m(θ) ୣሺകశഀሻ √ଶగ =e imα ϕn l m(r, θ,φ) (6-18) 于是 ܥመ(α) ۏ ێ ێ ێ ۍ ݀ ݀ଵ ݀ିଵ ݀ଶ ےଶ݀ି ۑ ۑ ۑ ې = ۏ ێ ێ ێ ۍ e୧ଶఈ 00 0 0 0 e୧ఈ 00 0 0 01 0 0 0 0 0eି୧ఈ 0 0 00 0 eି୧ଶఈے ۑ ۑ ۑ ې ۏ ێ ێ ێ ۍ ݀ ݀ଵ ݀ିଵ ݀ଶ ےଶ݀ି ۑ ۑ ۑ ې (6-19) 这个转动操作的特征标 χ(α)是 χ(α)=ei2α +eiα +ei0α +e-iα +e-i2α =2cos2α+2cosα+1 (6-20) 当 O 群的纯转动操作 Ê,Ĉ4,Ĉ2,Ĉ3 和 Ĉ'2 作用于 d 轨道上时,其变换矩阵的特征标分别为 χ(E)=5 χ(C2)=χ(ܥଶ ᇱ )=1 χ(C3)=െ1 χ(C4)=െ1 利用点群的可约表示向不可约表示分解的公式 ai= ଵ ఀ ோ χ(R)χi(R) (6-21) 将以五个 d 轨道为基底的可约表示 Γ 分解为不可约表示 aA1= ଵ ଶସ[5×1+6×(െ1)×1+3×1×1+8×(െ1)×l+6×1×l]=0 aA2= ଵ ଶସ[5×1+6×(െ1)×(-1)+3×1×1+8×(െ1)×1+6×1×(െ1)]=0 aE= ଵ ଶସ[5×2+6×(െ1)×0+3×l×2+8×(െ1)×(െ1) +6×l×0 =1 aT1= ଵ ଶସ[5×3+6×(െ1)×1+3×l×(െ1)+8×(െl)×0+6×1×(െ1)]=0 aT1= ଵ ଶସ[5×3×6×(െ1)×(െ1) +3×1×(െ1) +8×(െ1)×0+6×1×1]=1 这可表示为 Γ=e+t2 (6-22)

在(6-23)式中以小写英文字母e和2表示用不可约表示E和T来划分相应的原子轨道.由于d轨道在正八面 体Oh群中都是偶表示,故在Oh配位场中,中央离子d轨道分裂为: 「=egtl2g (6-23) 这表明,中央离子的d轨道在正八面体配位场作用下分裂成了两组,一组属于e2不可约表示,由表61可 知,d和d属于eg不可约表示.另一组属于2g不可约表示,由表6-1可知,dy,d,和d属于g不可 约表示 在正八面体配位场中,d,轨道的能量(以其自由离子为能量零点)由下列积分给出 △E(d=∫dVd.2dT (6-24) 为计算方便,(615)式可化为球坐标系的相应表达式 h-ggrsnasniprcspjrcosa-外+nr1ksmasmpreospyHeosia-3 (6-25) a 4a5 式中 g (6-26) a 35q 4a5 (6-27) 则 dR(rDr'[sinOsinocsindrE (6-28) 式中 AErn6R品acrt2a63cos0-lfsm6u0ug (6-29) △E=DgR3a(Odr2元6sinasmpcospHeos0-33cos0-lfsndu0up (6-30) 由于 ∫d2d.2dr=l (6-31) G、原3os0-snau0 (6-32) (sinp+cospdg=gr3+cg40io-手2ax 3 4 (6-33) (n-1.n-3. 42 后sin9d0=nsina-2a0 n n-2 51,n为奇数 2 n-1n-3 21. (6-34) nn-2…年乞艺,n为偶数 cos"0sinedo-1 +1 (6-35) 月cos00sin2m+n0a0 246…2m (6-36) (m+1)(n+3)…(m+2m+1) 可得 AEo-n=-5q (6-37 AEr=DgR2acrrdU径naHeosi0(ecosa-ifsinau0-3 (6-38) 对于0部分的积分有gC径im0-cos0(3cos20-1sin8u0-2Gsin0+cos0(3cos20-1'sn0u0 2子os低n0-3os6nm0rni0r9sincos0-6ecorn0+sin6cos0a0 153
153 在(6 -23)式中以小写英文字母 e 和 t2表示用不可约表示 E 和 T 来划分相应的原子轨道.由于 d 轨道在正八面 体 Oh 群中都是偶表示,故在 Oh 配位场中,中央离子 d 轨道分裂为: Γ=eg+t2g (6-23) 这表明,中央离子的 d 轨道在正八面体配位场作用下分裂成了两组,一组属于 eg不可约表示,由表 6-1 可 知,dz2和 dx2-y2属于 eg 不可约表示.另一组属于 t2g 不可约表示,由表 6-l 可知,dxy,dxz,和 dyz 属于 t2g 不可 约表示. 在正八面体配位场中,dz2轨道的能量(以其自由离子为能量零点)由下列积分给出 ΔE(dz2)=∫dz2Vdz2dτ (6-24) 为计算方便,(6-15)式可化为球坐标系的相应表达式 V=െ െଷହ ସఱ[r 4 sin4 θ(sin4 φ+cos4 φ)+r 4 cos 4 θെଷ ହ r 4 ]=r0+Dr4 [sin4 θ(sin4 φ+cos4 φ)+cos4 θെଷ ହ ] (6-25) 式中 r0=െ (6-26) D=െଷହ ସఱ (6-27) 则 ΔE(dz2)= ܴ ଶ ଶ ሺݎሻ ଶగ గ ஶ 5 8(3cos2 θെ1)2 ( ଵ √ଶగ) 2 {r0+Dr4 [sin4 θ(sin4 φ+cos4 φ)+cos4 θെଷ ହ ]}r 2 sinθdrdθdφ=ΔE0+ΔE1 (6-28) 式中 ΔE0=r0ܴ ଶ ଶ ሺݎሻ ஶ r 2 dr⋅ ଵ 5 ଶగ 8 ଶగ గ (3cos2 θെ1)2 sinθdθdφ (6-29) ΔE1=Dܴ ଶ ଶ ሺݎሻ ஶ r 4 ⋅r 2 dr⋅ ଵ ଶగ ሾ ଶగ గ sin4 θ(sin4 φ+cos4 φ)+cos4 θെଷ ହ ]× ହ ଼ (3cos2 θെ1)2 sinθdθdφ (6-30) 由于 ∫dz2dz2dτ=1 (6-31) ට5 8 గ (3cos2 θെ1)2 sinθdθ (6-32) ሺ ଶగ sin4 φ+cos4 φሻdφ= 3cos4߮ 4 ଶగ dφ= ଷ ସ ×2π (6-33) ߠ sin ഏ మ dθ= ିଵ ߠ ଶିsin ഏ మ dθ=ቐ ݊െ1 ݊ ⋅ ݊െ3 ݊െ2 ⋅⋯⋅ 4 5 ⋅ 2 3 ⋅ 1, ݊为奇数 ݊െ1 ݊ ⋅ ݊െ3 ݊െ2 ⋅⋯⋅ 2 4 ⋅ 1 2 ⋅ ߨ 2 , ݊为偶数 (6-34) ߠ cos ഏ మ sinθdθ= ଵ ାଵ (6-35) ߠ cos ഏ మ sin2m+1θdθ= ଶ⋅ସ⋅⋯ଶ ሺାଵሻሺାଷሻ⋯ሺାଶାଵሻ (6-36) 可得 ΔE0=r0=െ (6-37) ΔE1=Dܴ ଶ ଶ ሺݎሻ ஶ r 4 ⋅r 2 dr ହ ଼ ሼ ሺ గ ଷ ସ sin4 θ+cos4 θሻ(3cos2 θെ1)2 sinθdθെଷ ହ ሽ (6-38) 对于 θ 部分的积分有 ሺ గ ଷ ସ sin4 θ+cos4 θሻ(3cos2 θെ1)2 sinθdθ=2 ሺ ഏ మ ଷ ସ sin4 θ+cos4 θሻ(3cos2 θെ1)2 sinθdθ =2 ሺ ഏ మ ଶ ସ cos 4 θsin5 θെଽ ଶ cos 2 θsin5 θ+ ଷ ସ sin5 θ+9sinθcos 8 θെ6cos6 θsinθ+sinθcos 4 θሻdθ
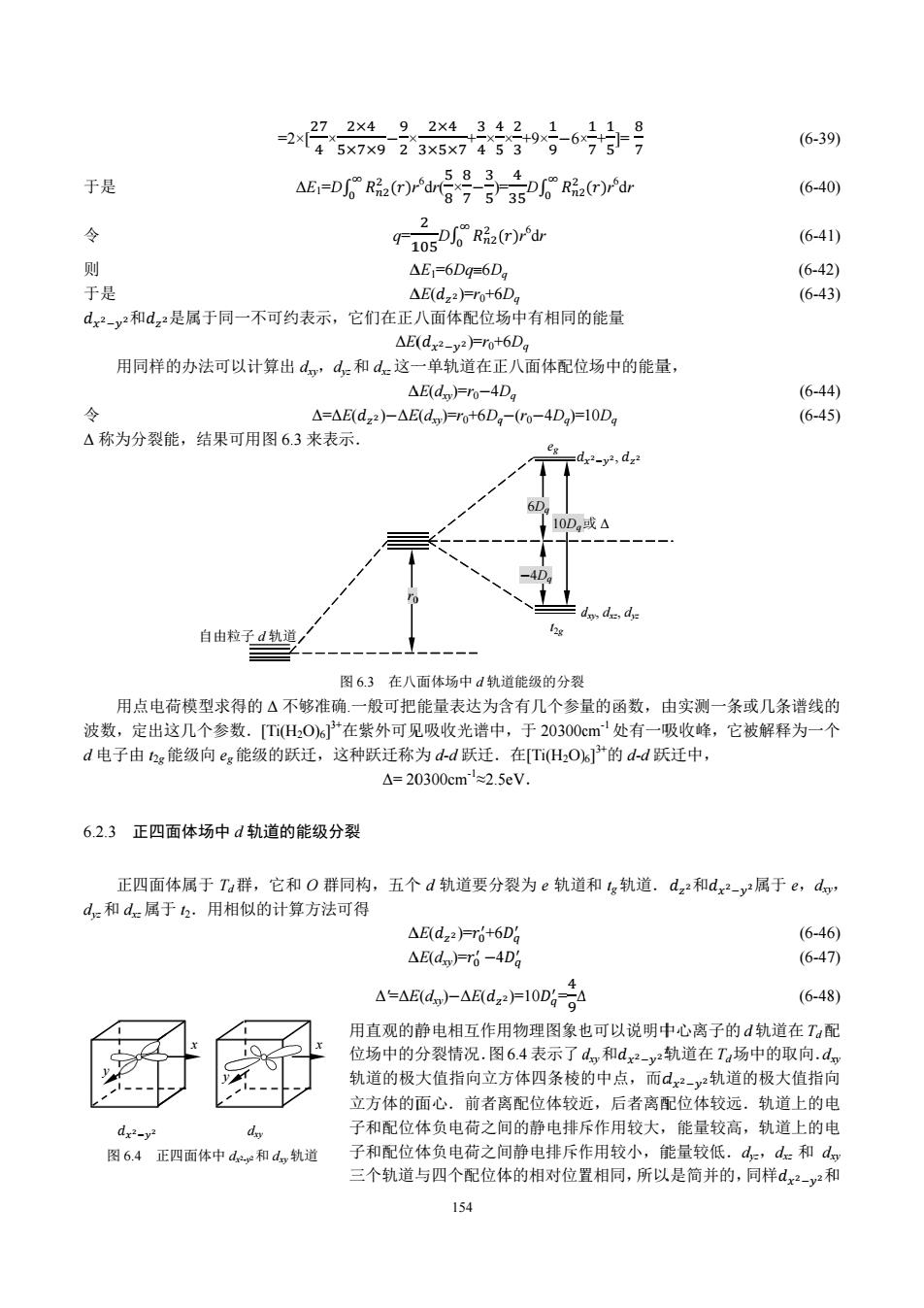
X2×492×4342.111-8 =2×45x7x923x5x7453 (6-39) 583.4 于是 △E1=DgR品2r)rd后 写于35D6R品2r)rdr (6-40) 87535 Ti05D%R品rdr 2 令 (6-41) 则 △E1=6Dq=6Dg (6-42) 于是 △E(dz2Fro+6Dg (6-43) dx2-y2和d22是属于同一不可约表示,它们在正八面体配位场中有相同的能量 △E(dx2-y2Fro+6Dg 用同样的办法可以计算出d,d,和d这一单轨道在正八面体配位场中的能量, △E(d=ro-4Dg (6-44) 令 △=AE(dz2)-△E(dFo+6Dg-(ro-4DgFl0Dg (6-45) △称为分裂能,结果可用图6.3来表示 esdxy,d 6D 10D,或A -4D do de,dy 自由粒子d轨道 12g 图6.3。在八面体场中d轨道能级的分裂 用点电荷模型求得的△不够准确.一般可把能量表达为含有几个参量的函数,由实测一条或几条谱线的 波数,定出这几个参数.TiH2O)6在紫外可见吸收光谱中,于20300cm处有一吸收峰,它被解释为一个 d电子由2g能级向eg能级的跃迁,这种跃迁称为d-d跃迁.在Ti(H2O6+的d-d跃迁中, △=20300cm'≈2.5eV. 6.2.3正四面体场中d轨道的能级分裂 正四面体属于Ta群,它和O群同构,五个d轨道要分裂为e轨道和1g轨道.dz2和dx2-y2属于e,d, d和d属于2.用相似的计算方法可得 △E(d22))=6+6Dg (6-46) △EdFT6-4Dg (6-47) A=AEd,△BdF10g-4 (6-48) 用直观的静电相互作用物理图象也可以说明中心离子的d轨道在T配 位场中的分裂情况.图6.4表示了d和dx2-y2轨道在Ta场中的取向.do 轨道的极大值指向立方体四条棱的中点,而dx2-y2轨道的极大值指向 立方体的面心.前者离配位体较近,后者离配位体较远.轨道上的电 dx2-y2 子和配位体负电荷之间的静电排斥作用较大,能量较高,轨道上的电 图6.4正四面体中dae和d轨道 子和配位体负电荷之间静电排斥作用较小,能量较低.d4,,d和d, 三个轨道与四个配位体的相对位置相同,所以是简并的,同样dx2-y2和 154
于是 令 则 于是 ݀௫మି௬మ和݀௭మ 用同样 令 Δ 称为分裂能 用点电荷 波数,定出这 d 电子由 t2g 6.2.3 正四面 正四面体 dyz 和 dxz 属于 ݀௫మି௬మ 图 6.4 正 y మ是属于同一 的办法可以计 能,结果可用 荷模型求得的 这几个参数. 能级向 eg 能 面体场中 d 轨 体属于 Td 群 于 t2.用相似 自由粒子 d 正四面体中 dx2-y y x =2×[ ଶ ସ × ΔE1=D 不可约表示 计算出 dxy, Δ=Δ 用图 6.3 来表 的 Δ 不够准确 [Ti(H2O)6] 3 能级的跃迁, 轨道的能级分 群,它和 O 群 似的计算方法 子 d 轨道 dxy y2和 dxy 轨道 x × ଶൈସ ହൈൈଽെଽ ଶ × Dܴ ଶ ଶ ሺݎሻ ஶ r q= ଵ Δ Δ ,它们在正八 ΔE( dyz和 dxz 这一 Δ ΔE(݀௭మ)െΔE 表示. 图 6.3 在八面 确.一般可把 3+ 在紫外可见 这种跃迁称为 Δ= 20 分裂 群同构,五个 法可得 Δ Δ Δ'=ΔE 用直观的静 位场中的分 轨道的极大 立方体的面 子和配位体 子和配位体 三个轨道与 r0 154 ଶൈସ ଷൈହൈ + ଷ ସ × ସ ହ r 6 dr( ହ ଼ × ଼ െଷ ହ )= ଶ ଵହ Dܴ ଶ ଶ ሺ ஶ ΔE1=6Dq6D ΔE(݀௭మ)=r0+6 八面体配位场 (݀௫మି௬మ)=r0+ 一单轨道在正 ΔE(dxy)=r0െ4D E(dxy)=r0+6Dq 面体场中 d 轨 能量表达为含 见吸收光谱中 为 d-d 跃迁. 0300cm -1≈2.5 个 d 轨道要分 ΔE(݀௭మ)=ݎ ᇱ +6 ΔE(dxy)=ݎ ᇱ െ4 E(dxy)െΔE(݀௭ 静电相互作用 分裂情况.图 大值指向立方 面心.前者离 体负电荷之间 体负电荷之间 与四个配位体 0 ସ ହ × ଶ ଷ +9× ଵ ଽ െ6× = ସ ଷହ Dܴ ଶ ஶ ଶ ሺݎሻr 6 dr Dq 6Dq 场中有相同的 +6Dq 正八面体配位 Dq qെ(r0െ4Dq)= 道能级的分裂 含有几个参量 中,于 20300c 在[Ti(H2O) 5eV. 分裂为 e 轨道 ܦ6 ᇱ ܦ4 ᇱ ௭మ)=10ܦ ᇱ = ସ ଽ Δ 用物理图象也 图 6.4 表示了 d 方体四条棱的 离配位体较近 间的静电排斥 间静电排斥作 体的相对位置 eg ݀ d t2g 10Dq 6Dq െ4Dq × ଵ + ଵ ହ ]= ଼ ሺݎሻr 6 dr 的能量 位场中的能量 10Dq 量的函数,由 cm -1 处有一吸 )6] 3+的 d-d 跃 道和 tg轨道. Δ 也可以说明中 dxy和݀௫మି௬మ轨 的中点,而݀ 近,后者离配 斥作用较大, 作用较小,能 置相同,所以 ௫మି௬మ, ݀௭మ dxy, dxz, dyz 或 Δ 量, 由实测一条或 吸收峰,它被 跃迁中, ݀௭మ和݀௫మି௬మ 中心离子的 d 轨道在 Td场 ݀௫మି௬మ轨道的 配位体较远. 能量较高, 能量较低.dy 以是简并的,同 (6-39 (6-40 (6-41 (6-42 (6-43 (6-44 (6-45 或几条谱线的 被解释为一个 మ属于 e,dxy, (6-46 (6-47 (6-48 d 轨道在 Td配 中的取向.dx 的极大值指向 轨道上的电 轨道上的电 yz,dxz 和 dx 同样݀௫మି௬మ和 ) 0) ) ) ) 4) ) 的 个 , ) ) ) 配 xy 向 电 电 xy 和

d,2也是简并的,量子力学可以证明,若选择与配位体电荷总量相等但呈均匀分布的球形对称的配位场中d 轨道能级为零点,则分裂后d轨道的能量和等于零,由此可得 Et,-E=A' (6-49) 3Et2+2Ee=0 (6-50) △=10Dg (6-51) 解由(6-49)、(6-50)、(6-51)所组成的方程组可得 E,5A=4D% (6-52) E=-A=-6D6 (6-53) 在正四面体场中,无论2轨道还是轨道都没有处于象正八面体场中那样的与配位体迎头相碰的位置,所 以在配位体和中央离子的距离相同时,应有△<△,由(6-48)式计算可得 44 40 SA-S10D,9D (6-54) 将(6-54)代入(6-52)和(6-53)式可得 E2=1.78Dg (6-55) E=-2.67Dg (6-56) 正四面体场中d轨道的能级分裂如图6.5所示.使甩同样的方法,可以得到其它点群配位场中d轨道的能级 分裂大小,其主要结果列于表6-2中.从中可知,场的对称性越低,d轨道分裂的组数越多. /5△ 自由粒子d轨道」 图6.5正T场中d轨能级的分裂 表6-2各种对称性场中d轨道的能量(Dg) 配位数场的对称性dx2-y2 dz2 dxy d dx 2 直线型 -6.28 10.28-6.28 1.14 1.14 3 三角形 5.46 -3.215.46 -3.86-3.86 4 正四面体 -2.67 -2.671.78 1.78 1.78 4 正方形 12.28 -4.282.28 -5.14-5.14 6 正八面体 6.00 6.00-4.00 -4.00-4.00 6.2.4高自旋态和低自旋态 对于同一能级上不同d轨道上的电子的排布,根据洪特规则,这时d电子将尽可能分占不同的d轨道 而保持自旋相互平行,量力学计算表明,满足洪特规则的体系能量最低.这表明当一个轨道已被一个电子 占据之后,若将第二个电子填入此轨道并与之配成对时,要克服电子之间的排斥而使体系钱量增加(保持 电子总数不变).这种克服电子间相互排斥作用所需要的能量称为电子成对能,以符号表示.络合物中心 离子d电子的排布将要考虑到两种因素的影响,即能级分裂和电子成对能的影响,分离能△的影响使电子 优先占据能量较低的轨道,电子成对能p的影响使电子尽可能分占不同的d轨道并保持自旋平行,当这两 种因素不发生矛盾时,只能得到一种电子排布.在正八面体场中,d',d2,d3,d8,d°和d10的电子排布分 155
155 ݀௭మ也是简并的,量子力学可以证明,若选择与配位体电荷总量相等但呈均匀分布的球形对称的配位场中 d 轨道能级为零点,则分裂后 d 轨道的能量和等于零,由此可得 ܧ௧మെEe=Δ' (6-49) 3ܧ௧మ+2Ee=0 (6-50) Δ'=10ܦ ᇱ (6-51) 解由(6-49)、(6-50)、(6-51)所组成的方程组可得 =௧మܧ ଶ ହ Δ'=4ܦ ᇱ (6-52) Ee=െ 3 5Δ'=െ6ܦ ᇱ (6-53) 在正四面体场中,无论 t2 轨道还是 e 轨道都没有处于象正八面体场中那样的与配位体迎头相碰的位置,所 以在配位体和中央离子的距离相同时,应有 Δ'<Δ,由(6-48)式计算可得 Δ'= ସ ଽ Δ= ସ ଽ ×10Dq= ସ ଽ Dq (6-54) 将(6-54)代入(6-52)和(6-53)式可得 ܧ௧మ=1.78Dq (6-55) Ee=െ2.67Dq (6-56) 正四面体场中 d 轨道的能级分裂如图 6.5 所示.使甩同样的方法,可以得到其它点群配位场中 d 轨道的能级 分裂大小,其主要结果列于表 6-2 中.从中可知,场的对称性越低,d 轨道分裂的组数越多. 图 6.5 正 Td 场中 d 轨能级的分裂 表 6-2 各种对称性场中 d 轨道的能量(Dq) 配位数 场的对称性 ݀௫మି௬మ ݀௭మ dxy dyz dxz 2 3 4 4 6 直线型 三角形 正四面体 正方形 正八面体 െ6.28 5.46 െ2.67 12.28 6.00 10.28 െ3.21 െ2.67 െ4.28 6.00 െ6.28 5.46 1.78 2.28 െ4.00 1.14 െ3.86 1.78 െ5.14 െ4.00 1.14 െ3.86 1.78 െ5.14 െ4.00 6.2.4 高自旋态和低自旋态 对于同一能级上不同 d 轨道上的电子的排布,根据洪特规则,这时 d 电子将尽可能分占不同的 d 轨道 而保持自旋相互平行,量力学计算表明,满足洪特规则的体系能量最低.这表明当一个轨道已被一个电子 占据之后,若将第二个电子填入此轨道并与之配成对时,要克服电子之间的排斥而使体系钱量增加(保持 电子总数不变).这种克服电子间相互排斥作用所需要的能量称为电子成对能,以符号 p 表示.络合物中心 离子 d 电子的排布将要考虑到两种因素的影响,即能级分裂和电子成对能的影响,分离能 Δ 的影响使电子 优先占据能量较低的轨道,电子成对能 p 的影响使电子尽可能分占不同的 d 轨道并保持自旋平行,当这两 种因素不发生矛盾时,只能得到一种电子排布.在正八面体场中,d 1,d 2,d 3,d 8,d 9 和 d 10 的电子排布分 t2 Δ'= ସ ଽ Δ 2/5Δ' r0 自由粒子 d 轨道 e 3/5Δ

别为:(g)'(eg°,(2g)(eg°,(2g(eg)°,(2g)(eg)2,(2g)(eg)3和(2g)(eg).当这两种因素矛盾时,根据△>p还 是△印可得到两种电子排布,正八面体场中d4,d,d和d'便属于这种情形.当△>p时,电子应尽可能填 入能量较低的轨道,这时来配对电子数较少,属于低自旋态.当△p(15000cm), 是强场络合物,中心离子d电子采取(2g)()°排布,属于低自旋态,一些正八面体络合物的自旋态如表6-3 所示. 表6-3 某些正八面体络合物的自旋状态 自旋状态 d" 中央离子 p(cm) 配位体 △(cm) 理论实验 3d+ Cr2+ 23500 6H20 13900 高 高 Mn2+ 28000 6H20 21000 高 高 3d3 Mn2+ 25500 6H20 7800 高 高 Fe3升 30000 6H20 13700 高 高 3d6 Fe2+ 15000 6H20 10400 高 高 Fe2+ 15000 6CN 33000 低 低 Co3+ 21000 6F 13000 高 高 C04 21000 6NH; 23000 低 低 3d7 Co2+ 22500 6H30 9300 高 高 在配位体场的作用下,中央离子d轨道能级发生分裂.这就可能发生电子在不同能量d轨道之间的跃 迁,这种跃迁称为d-d跃迁.dd跃迁的频率一在紫外及可见波段,所以过渡金属的络合物一般都具有颜色, 颜色的不同和分裂能的大小有直接关系,例如水溶液巾络离子[TiH0)63*在4927A(20400cm)处有一最大 吸收峰,因而分裂能△为20400cm,这就是电子从2轨道跃迁到e.轨道所吸收的能量.因为]吸收了蓝绿 光,所以它呈紫红色。 对于同一金属离子,分裂能△随配位体不同而变化,其大致顺序为: I「<Br<CI<SCN<F<OH~NO~HCOO<C2O4<HO<EDTA<吡啶~NH <乙二胺~二乙三胺<SO,2<联吡啶<NO2<CN 这个顺序称为光谱化学顺序. 对相同的配位体和同一金属离子,高价离子的分裂能比低价离子的大,例如[F©(HO)6]+和[Fe(HO)6+, △值分别为13700cm和10400cm故前者的颜色比后者的深. 6.2.5晶体场稳定化能(CFSE) 中央离子d电子处于未分裂的d轨道的总能量和它们进入分裂的d轨道后的总能量之差,即d电子从 未分裂的d轨道进入分裂的d轨道所产生的总能量下降值称为晶体场稳定化能(CFSE), 它表征了络合物的稳定性,例如Fe2,在弱正八面体配位场中,采取(12g)(e)2的高自旋态排布,故其晶 体场稳定化能为 CFSE=0-(4E12g+2Ee)=-4×(-4D)-2×6D,=4D, (6-57) Fe2+在强正八面体配缸场中,采取(2g)()°的低自旋排布态其晶体场稳定化能为 CFSE=0-6Eh2g-2p-0-6×(-4Dg)-2p-24Dg-2p (6-58) 络合物的热力学稳定性可用晶体场稳定化能来解释,第三周期过渡元素二价离子六水合物MH,O% 的水化热(一△H)可表示为 M2(气)+6HO(液)→MHO)6(溶液)+(-△H0 156
156 别为:(t2g) 1 (eg) 0 ,(t2g) 2 (eg) 0 ,(t2g) 3 (eg) 0 ,(t2g) 6 (eg) 2 ,(t2g) 6 (eg) 3 和(t2g) 6 (eg) 4 .当这两种因素矛盾时,根据 Δ>p 还 是 Δp 时,电子应尽可能填 入能量较低的轨道,这时来配对电子数较少,属于低自旋态.当 Δp(15000cm-1), 是强场络合物,中心离子 d 电子采取(t2g) 6 (eg) 0排布,属于低自旋态,一些正八面体络合物的自旋态如表 6-3 所示. 表 6-3 某些正八面体络合物的自旋状态 d n 中央离子 p(cm-1) 配位体 Δ(cm-1) 自旋状态 理论 实验 3d 4 3d 5 3d 6 3d 7 Cr2+ Mn2+ Mn2+ Fe3+ Fe2+ Fe2+ Co3+ Co3+ Co2+ 23500 28000 25500 30000 15000 15000 21000 21000 22500 6H2O 6H2O 6H2O 6H2O 6H2O 6CN- 6F- 6NH3 6H2O 13900 21000 7800 13700 10400 33000 13000 23000 9300 高 高 高 高 高 低 高 低 高 高 高 高 高 高 低 高 低 高 在配位体场的作用下,中央离子 d 轨道能级发生分裂.这就可能发生电子在不同能量 d 轨道之间的跃 迁,这种跃迁称为 d-d 跃迁.d-d 跃迁的频率一在紫外及可见波段,所以过渡金属的络合物一般都具有颜色, 颜色的不同和分裂能的大小有直接关系,例如水溶液巾络离子[Ti(H2O)6] 3+在 4927Ǻ(20400cm-1)处有一最大 吸收峰,因而分裂能 Δ 为 20400cm-1,这就是电子从 t2 轨道跃迁到 eg 轨道所吸收的能量.因为]吸收了蓝绿 光,所以它呈紫红色。 对于同一金属离子,分裂能 Δ 随配位体不同而变化,其大致顺序为: I - <Br- <C1- <SCN- <F- < OH- ~NO- ~HCOO- <C2O4 - <H2O<EDTA<吡啶~NH3 <乙二胺~二乙三胺<SO3 2-<联吡啶<NO2 - <CN- 这个顺序称为光谱化学顺序. 对相同的配位体和同一金属离子,高价离子的分裂能比低价离子的大,例如[Fe(H2O)6] 3+和[Fe(H2O)6] 2+, Δ 值分别为 13700cm-1 和 10400cm-1 故前者的颜色比后者的深. 6.2.5 晶体场稳定化能(CFSE) 中央离子 d 电子处于未分裂的 d 轨道的总能量和它们进入分裂的 d 轨道后的总能量之差,即 d 电子从 未分裂的 d 轨道进入分裂的 d 轨道所产生的总能量下降值称为晶体场稳定化能(CFSE). 它表征了络合物的稳定性,例如 Fe2+,在弱正八面体配位场中,采取(t2g) 4 (eg) 2 的高自旋态排布,故其晶 体场稳定化能为 CFSE=0െ(4Et2g+2Ee)=െ4×(െ4Dq)െ2×6Dq=4Dq (6-57) Fe2+在强正八面体配缸场中,采取(t2g) 6 (eg) 0 的低自旋排布态其晶体场稳定化能为 CFSE=0െ6Et2gെ2p=0െ6×(െ4Dq)െ2p=24Dqെ2p (6-58) 络合物的热力学稳定性可用晶体场稳定化能来解释,第三周期过渡元素二价离子六水合物[M(H2O)6] 2+ 的水化热(െΔH)可表示为 M2+(气)+6H2O(液)→[M(H2O)6] 2+(溶液)+(െΔH)

实验测定结果如图6.6所示(实线)。 由于中央离子核电荷从Ca到Zn逐步增加,3d电 子壳层逐步缩小,因而极性水分子和中央离子的距离就 逐渐缩短,故水化作用也应逐渐加强.从静电作用来看, 其水化热应随d电子数的增加而逐渐上升,呈一平滑曲 线(图6.6中的虚线).但实际的曲线却是一条双蜂曲 线,将图6.6中的平滑虚线对应的-△H值,加上各dP 组态在弱正八面体场中的各CFSE值,结果正好就是实 图6.6离子水化热与d电子数的关系 验测得的双峰曲线 6.2.6络合物的畸变和姜-泰勒Jahn-Teller)效应 1937年H.A.Jahn和E.Teller指出:在对称的非线型分子中,如果体系的基态有几个简并能级,则体系 是不稳定的,它一定要发生畸变,使体系简并解除,而稳定于较低能级的构型.这就是Jahn-Teller效应, 具有d9结构的中央离子,在正八面体配位场中,具有(g)(dx2-y2)'(dz2)》2和(2g)(dx2-y2)(dz2)'两种可能的 排布,它们县有相同的能量,即体系处于二度简并状态,按Jahn-Teller效应,体系几何构型要发生畸变而 稳定于一种构型.d°比d10少1个电子,d具有理想的正八面体构型. 如d°是去掉d0中c2上的一个电子,即(dx2-y2)'(dz2)》2排布,这就减小了对x轴和y轴上配位体的排斥 力,使x和±y方向上四个配位体能够内移,形成四个较短的键:而在:轴上的两个配位体则相对要到了较 大的排斥力而形成两个较长的键,这.样的畸变使得dz2轨道的能量升高,dx2-y2轨道能量下降,消除了简 并.对于采取(2g)(dx2-y2)(dz2)'排布的d°结构,类似的讨论得出应形成四个较长的键和两个较短的键,正 八面体络合物中央离子2g轨道出现简并时,也会发生畸变,但其畸变程度较小.[C(HO)6的几何构型为 拉长了的八面体,其稳定化能比正八面体的稳定化能高,因而C+的水化热也大.这就解释了图6.6中双蜂 曲线在d4处有一最大值这一现象. 晶体场理论在解释络合物的颜色,磁性和立体构型方面取得了很大成功,但在解释光谱化学顺序、有 机烯络合物的形成、羰基络合物的稳定性方面还显得无能为力.为了说明这些现象,络台物的分子轨道理 论产生了. 6.3络合物的分子轨道理论 6.3.1配位体群轨道 按照分子轨道理论,络合物的单电子波函数(分子轨道)是中央原子的原子轨道和配位体的原子轨道 (或分子轨道)的线性组合,它属于络合物所属点群的不可约表示.于是络合物的分子轨道必须由属于同 一不可约表示的中心原子(或离子)的轨道和配位体的轨道线性组合而成,正八面体络合物是属于O2点群, 由O%群的特征标表可知,中央原子的s轨道属于a1g不可约表示,px,p,p-属于t1u不可约表示,(n-1)d2 和(n-1)dx2-y2属于eg可约表示,d,d,=,d属于2g不可约表示,将配位体轨道线性组合成属于O群不可 约表示的群轨道,最后将属于同一不可约表示的中心原子的原子轨道和配位体群轨道线性组合成络合物的 分子轨道,下面讨论正八面体络合物的σ轨道. 坐标系如图67所示,现说明如下: (1)中心原子M的坐标系x,少,采用右手定则. (2)六个配位体位于中心离子坐标系的坐标轴上,并将x,y,:轴正方向上的配位体编号为L1,L2和L 157
157 实验测定结果如图 6.6 所示(实线)。 由于中央离子核电荷从 Ca 到 Zn 逐步增加,3d 电 子壳层逐步缩小,因而极性水分子和中央离子的距离就 逐渐缩短,故水化作用也应逐渐加强.从静电作用来看, 其水化热应随 d 电子数的增加而逐渐上升,呈一平滑曲 线(图 6.6 中的虚线).但实际的曲线却是一条双蜂曲 线,将图 6.6 中的平滑虚线对应的െΔH 值,加上各 dn 组态在弱正八面体场中的各 CFSE 值,结果正好就是实 验测得的双峰曲线. 6.2.6 络合物的畸变和姜-泰勒(Jahn-Teller)效应 1937 年 H.A.Jahn 和 E.Teller 指出:在对称的非线型分子中,如果体系的基态有几个简并能级,则体系 是不稳定的,它一定要发生畸变,使体系简并解除,而稳定于较低能级的构型.这就是 Jahn-Teller 效应, 具有 d 9 结构的中央离子,在正八面体配位场中,具有(t2g) 6 (݀௫మି௬మ) 1 (݀௭మ) 2 和(t2g) 6 (݀௫మି௬మ) 2 (݀௭మ) 1 两种可能的 排布,它们县有相同的能量,即体系处于二度简并状态,按 Jahn-Teller 效应,体系几何构型要发生畸变而 稳定于一种构型.d 9 比 d 10 少 1 个电子,d 10 具有理想的正八面体构型. 如 d 9 是去掉 d 10 中 c2 上的一个电子,即(݀௫మି௬మ) 1 (݀௭మ) 2 排布,这就减小了对 x 轴和 y 轴上配位体的排斥 力,使±x 和±y 方向上四个配位体能够内移,形成四个较短的键;而在 z 轴上的两个配位体则相对要到了较 大的排斥力而形成两个较长的键,这.样的畸变使得݀௭మ轨道的能量升高,݀௫మି௬మ轨道能量下降,消除了简 并.对于采取(t2g) 6 (݀௫మି௬మ) 2 (݀௭మ) 1 排布的 d 9 结构,类似的讨论得出应形成四个较长的键和两个较短的键,正 八面体络合物中央离子 t2g 轨道出现简并时,也会发生畸变,但其畸变程度较小.[Cr(H2O)6] 2+的几何构型为 拉长了的八面体,其稳定化能比正八面体的稳定化能高,因而 Cr2+的水化热也大.这就解释了图 6.6 中双蜂 曲线在 d 4 处有一最大值这一现象. 晶体场理论在解释络合物的颜色,磁性和立体构型方面取得了很大成功,但在解释光谱化学顺序、有 机烯络合物的形成、羰基络合物的稳定性方面还显得无能为力.为了说明这些现象,络台物的分子轨道理 论产生了. 6.3 络合物的分子轨道理论 6.3.1 配位体群轨道 按照分子轨道理论,络合物的单电子波函数(分子轨道)是中央原子的原子轨道和配位体的原子轨道 (或分子轨道)的线性组合,它属于络合物所属点群的不可约表示.于是络合物的分子轨道必须由属于同 一不可约表示的中心原子(或离子)的轨道和配位体的轨道线性组合而成,正八面体络合物是属于 O2 点群, 由 Oh 群的特征标表可知,中央原子的 ns 轨道属于 a1g 不可约表示,npx,npy,npz属于 t1u 不可约表示,(nെ1)݀௭మ 和(nെ1)݀௫మି௬మ属于 eg 可约表示,dxy,dyz,dxz属于 t2g 不可约表示,将配位体轨道线性组合成属于 Oh 群不可 约表示的群轨道,最后将属于同一不可约表示的中心原子的原子轨道和配位体群轨道线性组合成络合物的 分子轨道,下面讨论正八面体络合物的 σ 轨道. 坐标系如图 6.7 所示,现说明如下: (1)中心原子 M 的坐标系 x,y,z 采用右手定则. (2)六个配位体位于中心离子坐标系的坐标轴上,并将 x,y,z 轴正方向上的配位体编号为 L1,L2和 L3 图 6.6 离子水化热与 d 电子数的关系 350 400 450 500 550 d10 d5 d0 Ca Mn Zn