
第五章多原子分子 .125 5.1从头计算法(ab initio).125 5.l.1哈特利-福克-罗汤(Hartree-.Fock-Roothaan)方程(HFR方程) 125 5.1.2从头计算法 .126 5.1.3基函数的选择 .127 5.2分子轨道的近似计算方法 .128 52.1CND0法. .128 5.2.2EHM0法. .128 5.3 Huckel分子轨道法. 129 5.3.1 Huckel近似. 129 53.2丁二烯HMO久期方程的解 130 5.3.3离域能 131 5.4HMO方法的应用 132 5.4.1链共轭多烯和单环平面共轭多烯 132 5.4.2无机共轭分子 …133 5.4.3离域π键形成的条件 .133 5.4.4电荷密度… 134 5.4.5键级. .134 5.4.6自由价 .135 5.4.7分子图. 135 5.5杂化轨道理论 136 5.5.1杂化轨道 136 5.5.2杂化轨道中的系数 137 5.53p,p和sp3等性杂化轨道 138 5.5.4不等性杂化轨道. .139 5.5.5d.-S-p杂化 140 5.6离域分子轨道和定域分子轨道 .140 5.6.1两种分子轨道的特点.. 140 5.6.2两种分子轨道间的变换 141 5.7缺电子分子和多中心键 143 5.7.1硼烷的电子结构 143 5.7.2其它缺电子分子 144 5.8分子的几何构型… 145 5.8.1三原子分子的几何构型一沃尔斯(Walsh)规则. .145 5.8.2多原子分子的几何构型一一价电子对互斥理论. .146 .…, .147
1 第五章 多原子分子 ............................................................................................................................................. 125 5.1 从头计算法(ab initio) ................................................................................................................................ 125 5.1.1 哈特利-福克-罗汤(Hartree-Fock-Roothaan)方程 方程) ........................................................... 125 5.1.2 从头计算法 ......................................................................................................................................... 126 5.1.3 基函数的选择 ..................................................................................................................................... 127 5.2 分子轨道的近似计算方法 ........................................................................................................................ 128 5.2.1 CNDO 法 ............................................................................................................................................. 128 5.2.2 EHMO 法 ............................................................................................................................................ 128 5.3 Huckel 分子轨道法 .................................................................................................................................... 129 5.3.1 Huckel 近似 ......................................................................................................................................... 129 5.3.2 丁二烯 HMO 久期方程的解 .............................................................................................................. 130 5.3.3 离域能 ................................................................................................................................................. 131 5.4 HMO 方法的应用 ...................................................................................................................................... 132 5.4.1 链共轭多烯和单环平面共轭多烯 ..................................................................................................... 132 5.4.2 无机共轭分子 ..................................................................................................................................... 133 5.4.3 离域 π 键形成的条件 ......................................................................................................................... 133 5.4.4 电荷密度 ............................................................................................................................................. 134 5.4.5 键级 ..................................................................................................................................................... 134 5.4.6 自由价 ................................................................................................................................................. 135 5.4.7 分子图 ................................................................................................................................................. 135 5.5 杂化轨道理论 ............................................................................................................................................ 136 5.5.1 杂化轨道 ............................................................................................................................................. 136 5.5.2 杂化轨道中的系数 ............................................................................................................................. 137 5.5.3 sp,sp 2和 sp 3 等性杂化轨道 ................................................................................................................. 138 5.5.4 不等性杂化轨道 ................................................................................................................................. 139 5.5.5 d-s-p 杂化 ............................................................................................................................................ 140 5.6 离域分子轨道和定域分子轨道 ................................................................................................................ 140 5.6.1 两种分子轨道的特点 ......................................................................................................................... 140 5.6.2 两种分子轨道间的变换 ..................................................................................................................... 141 5.7 缺电子分子和多中心键 ............................................................................................................................ 143 5.7.1 硼烷的电子结构 ................................................................................................................................. 143 5.7.2 其它缺电子分子 ................................................................................................................................. 144 5.8 分子的几何构型 ........................................................................................................................................ 145 5.8.1 三原子分子的几何构型—沃尔斯(Walsh)规则 ................................................................................. 145 5.8.2 多原子分子的几何构型——价电子对互斥理论 .............................................................................. 146 习题 ..................................................................................................................................................................... 147 (HFR

第五章 多原子分子 适用于研究多原子分子电子结构的理论分为分子轨道理论和价键理论.本章先讨论分子轨道理论的各 种计算方法,然后简单介绍价键理论 5.1从头计算法(ab initio) 用分子轨道理论处理分子电子结构问题的精确方法当推为从头计算法(ab initio)。从头计算法一般采用 下面四个基本近似:(I)Bom-Oppenheimer近似,(2)非相对论近似,(3)单电子近似,(4)LCAO-MO近似.在 这些近似的基础上,用自治场方法精确求解哈特利-福克-罗汤(Hartree-Fock-Roothaan)方程,即为从头计算法. 5.l.1哈特利-福克-罗汤Hartree-Fock-Roothaan)方程(HFR方程) 从头计算法采用LCAO-MO近似,即把分子轨道表示为原子轨道的线性组合: =∑cn中u (5-1) 其中{中}常选为实的基函数组,一般中是归一化的,但不正交,对于多电子原子体系中的单电子波函数, 我们在2.3节曾推导出,它们各满足一个单电子方程一Hartree-Fock方程(2-69).按照完全相同的方法,同 样能推导出分子体系的单电子波函数中,也满足Hartree-.Fock方程 F(1)p.1=e(1) (5-2) 其中Fock算符 (1)片=A+∑1)-(1明 (5-3) 只是在分子体系中有多个原子核,且单电子波函数是分子轨道中,所以.A,了(1)和R(1)的定义应该是: e-好-器 (5-4) 01o*2,220四 (5-5) 1 R0042a2dM0) (5-6) 式中m为原子核的标号, 为了确定分子的电子结构,需要计算分子轨道中,和轨道能量E1,在LCAO-MO近似下,分子轨道 是由原子轨道的组合系数c,决定的,需要解含有c,的HFR方程.HFR方程的精确推导,需要把=∑c中如 代入到分子总能量E的表达式,将E对c变分,利用分子轨道的正变归一化条件,由E取极小值即可得到 HFR方程.这种推导方法比较繁锁,可以采用简单的但不太严格的方法得到HFR方程, 把(5-1)式代入(5-2)式,得 E()∑cu中u=e,∑c中u (5-7) 用中,*左乘上式两边,并对电子坐标变量积分,得 ∑cΦ,*(1)E(I)φ1)dv1-el中,(I)中1)d]=0 (5-8) 125
125 第五章 多原子分子 适用于研究多原子分子电子结构的理论分为分子轨道理论和价键理论.本章先讨论分子轨道理论的各 种计算方法,然后简单介绍价键理论. 5.1 从头计算法(ab initio) 用分子轨道理论处理分子电子结构问题的精确方法当推为从头计算法(ab initio)。从头计算法一般采用 下面四个基本近似:(1)Born-Oppenheimer 近似,(2)非相对论近似,(3)单电子近似,(4) LCAO-MO 近似.在 这些近似的基础上,用自治场方法精确求解哈特利-福克-罗汤(Hartree-Fock-Roothaan)方程,即为从头计算法. 5.1.1 哈特利-福克-罗汤(Hartree-Fock-Roothaan)方程(HFR 方程) 从头计算法采用 LCAO-MO 近似,即把分子轨道表示为原子轨道的线性组合: ψi= cμiϕμ (5-1) 其中{ϕμ}常选为实的基函数组,一般 ϕμ 是归一化的,但不正交,对于多电子原子体系中的单电子波函数, 我们在 2.3 节曾推导出,它们各满足一个单电子方程——Hartree-Fock 方程(2-69).按照完全相同的方法,同 样能推导出分子体系的单电子波函数 ψi 也满足 Hartree-Fock 方程 ܨ (1)ψi(1)=∈iψi(1) (5-2) 其中 Fock 算符 ܨ (1)=ܪଵ+ j ܬ] መ (1)െܭ)1)] (5-3) 只是在分子体系中有多个原子核,且单电子波函数是分子轨道 ψ,所以.ܪଵ,ܬ መ (1)和ܭ)1)的定义应该是: ܪଵ=െ 1 2 ଵ ଶ െ ܼ݉ 1݉ݎ (5-4) ܬ መ (1)ψi(1)=[∫ψi*(2) ଵ భమ ψj(2)dv2]ψi(1) (5-5) ܭ)1)ψi(1)=[∫ψj*(2) ଵ భమ ψi(2)dv2]ψi(1) (5-6) 式中 m 为原子核的标号. 为了确定分子的电子结构,需要计算分子轨道 ψi 和轨道能量∈1,在 LCAO-MO 近似下,分子轨道 ψi 是由原子轨道的组合系数 cμi 决定的,需要解含有 cμi 的 HFR 方程.HFR 方程的精确推导,需要把 ψi= cμiϕμ 代入到分子总能量 E 的表达式,将 E 对 cμi 变分,利用分子轨道的正变归一化条件,由 E 取极小值即可得到 HFR 方程.这种推导方法比较繁锁,可以采用简单的但不太严格的方法得到 HFR 方程, 把(5-1)式代入(5-2)式,得 ܨ (1) cμiϕμ=∈i cμiϕμ (5-7) 用 ϕv*左乘上式两边,并对电子坐标变量积分,得 cμi[∫ϕv*(1)ܨ (1)ϕμ(1)dv1െ∈i∫ϕv*(1)ϕμ(1)dv1]=0 (5-8)

令 Fw=∫φ*(1)F(I)冲(1)dv1 (5-9) Su=∫中,*(I)冲(I)dv1 (5-10) 利用这两个定义式可简化(5-8)式,即 cuFr-ESm=0(U=1.2....N:v=1.2....N) (5-11) 这就是Hartre-Fock-Roothaan方程(HFR方程),或简称为Roothaan方程.其中N为(5-l)式中基函数中u的个 数.HFR方程是由N个方程所构成的方程组,这种推导HFR方程的方法之所以不严格,是因为我们没有证 明由该方程所确定的cw能保证总能量取极小值. 利用F(1),了(1)和R(1)的定义式,可用原子轨道或基函数来表示F,u。 令 F=∫中,*(1)[a1+Uj(1)-E(1)川φ(1)dv1 =可o,*l)A1p1d+∑fb,cy中*22∑c中.(2d]p1 T126 -l(c.r.1c(n 令 h=∫中,*(1)A1中(I)dv1 (5-12) (vuPa)-时b,1冲k12*2帅2dnd (5-13) 则 F=hm+∑∑[∑c*colI(VplAa)-(oi (5-14) 占据 令 Pa=∑c4*cgi (5-15) 所有这些下标v,u,o,入的取值都是从1到N,所以F4,hu,Pa都可构成矩阵。由矩阵元Fu所构成的 矩阵为Fock矩阵,hw一构成的为Hamilton矩阵,Paa构成的为密度矩阵 由(5-l4)式可知,Fu中含有待定的系数ca,c,*,故Roothaan方程也须用自治场方法求解.入 5.1.2从头计算法 在Borm-Oppenheimer近似、非相对论近似和单电子近似的基础上,把分子轨道表示成原予轨道或基函 数的线性组合,则分子体系的Schrodinger方程演变为Roothaan方程,如果不再引入新的简化或近以,精确 求解Roothaan方程,这种计算方法则称为从头计算法.从头计算法在理论和方法上都比较严格,是目前最 精确的量子化学计算方法. 对于分子的计算,由于从头计算法采用了单电子近似(轨道近似),所以从头计算法是一种分子轨道法, 用从头计算法可以解出分子轨道能量∈,分子轨道,由中:可以得到分子的总波函数平,由平可以计算分 子的各种力学量的平均值,即得到分子的各种性质,例如,从分子的占据轨道可以直接利用下式计算分子 各点的电子密度p(r): pr=∑n,r)*r) (5-15) 式中,为轨道,的电子占据数.电子密度对于了解分子的成键情况和化学性质都是重要的,再例如,假定 在电子电离和激发跃迁的过程中,其它电子状态保持不变(这称为冻结近似),则电子的电离能山,和跃迁能 △E分别为 I=-E (5-16) △E=e-Ei (5-17) 即电离能近似为轨道能量的负值,跃迁能近似为轨道能量之差.这就是Koopmans定理. 在分子各种力学量平均值的计算中,分子总能量的计算具有基本的意义,由总能量最小值可以确定分 126
126 令 Fvμ=∫ϕv*(1)ܨ (1)ϕμ(1)dv1 (5-9) Sμv=∫ϕv*(1)ϕμ(1)dv1 (5-10) 利用这两个定义式可简化(5-8)式,即 cμiFvμെ∈iSμv=0 (μ=1,2,…,N;v=1,2,…,N) (5-11) 这就是 Hartre-Fock-Roothaan 方程(HFR 方程),或简称为 Roothaan 方程.其中 N 为(5-1)式中基函数 ϕμ的个 数.HFR 方程是由 N 个方程所构成的方程组,这种推导 HFR 方程的方法之所以不严格,是因为我们没有证 明由该方程所确定的 cμi能保证总能量取极小值. ܨ利用 ܬ,(1( መ (1)和ܭ)1)的定义式,可用原子轨道或基函数来表示 Fvμ。 令 Fvμ=∫ϕv*(1)[ܪଵ+ j ܬ) መ (1)െܭ)1))]ϕμ(1)dv1 =∫ϕv*(1)ܪଵ1ϕμ(1)dv1+ j ∫ϕv*(1)[∫ cλj*ϕλ*(2) ଵ భమ cσjϕσ(2)dv2]ϕμ(1)dv1 െ j ∫ϕv*(1)[∫ cλj*ϕλ*(2) ଵ భమ ϕμ(2)dv2] cσjϕσ(1)dv1 令 hvμ=∫ϕv*(1)ܪଵϕμ(1)dv1 (5-12) (vμ|λσ)=∫ϕv*(1)ϕμ(1) ଵ భమ ϕλ*(2)ϕσ(2)dv1dv2 (5-13) 则 Fvμ=hvμ+ [ j cλj*cσj][(vμ|λσ)െ(vσ|λμ)] (5-14) 令 Pσλ= 占据 j cλj*cσj (5-15) 所有这些下标 v,μ,σ,λ 的取值都是从 1 到 N,所以 Fvμ,hvμ,Pσλ都可构成矩阵。由矩阵元 Fvμ所构成的 矩阵为 Fock 矩阵,hvμ一构成的为 Hamilton 矩阵,Pσλ构成的为密度矩阵. 由(5-14)式可知,Fvμ中含有待定的系数 cσj,cλj*,故 Roothaan 方程也须用自冶场方法求解.λ 5.1.2 从头计算法 在 Born-Oppenheimer 近似、非相对论近似和单电子近似的基础上,把分子轨道表示成原予轨道或基函 数的线性组合,则分子体系的 Schrödinger 方程演变为 Roothaan 方程,如果不再引入新的简化或近以,精确 求解 Roothaan 方程,这种计算方法则称为从头计算法.从头计算法在理论和方法上都比较严格,是目前最 精确的量子化学计算方法. 对于分子的计算,由于从头计算法采用了单电子近似(轨道近似),所以从头计算法是一种分子轨道法, 用从头计算法可以解出分子轨道能量∈i,分子轨道 ψi,由 ψi可以得到分子的总波函数 Ψ,由 Ψ 可以计算分 子的各种力学量的平均值,即得到分子的各种性质,例如,从分子的占据轨道可以直接利用下式计算分子 各点的电子密度 ρ(r): ρ(r)= i niψi(r)*ψi(r) (5-15) 式中 ni 为轨道 ψi 的电子占据数.电子密度对于了解分子的成键情况和化学性质都是重要的,再例如,假定 在电子电离和激发跃迁的过程中,其它电子状态保持不变(这称为冻结近似),则电子的电离能 Ii 和跃迁能 Δ∈分别为 Ii =െ∈i (5-16) Δ∈=∈jെ∈i (5-17) 即电离能近似为轨道能量的负值,跃迁能近似为轨道能量之差.这就是 Koopmans 定理. 在分子各种力学量平均值的计算中,分子总能量的计算具有基本的意义.由总能量最小值可以确定分

子的键长和键角,即确定分子的几何构型;对于化学反应的研究,可以计算由反应物向产物转变过程中各 原子坐标不同位置的总能量,并得到总能量曲面(习惯上称为势能面),由这张曲面可以了解反应路径,活 化能、过渡态等信息, 5.1.3基函数的选择 基函数组(简称基组)是分子轨道展开的基础,基组选择的好坏对于$C℉计算结果至关重要,为了得 到精确的计算结果,一般需要选择较大的基组.若基函数的数目为N,则计算量与W4成正比.在实际计算 中,常根据需要来确定基组,不能一味追求精确度而招致过大的计算量.现在,最常用的是Slater函数基组 和Gauss函数基组. 1)Slater函数基组 Slater函数基组即Slater型轨道(STO)[见(2-79)式]。 中nlm=N,'eY1nm(0,p) (5-18) 式中N为归一化常数 N,=(202+12W2m元 (5-19) C为轨道指数,可用Slater函数作原子的SCF计算,根据使总能量最低的原则确定各原子轨道的C.n,l,m对 应于原子轨道的三个量子数.Slater基组可分为下列几种: (1)极小基组:分子中原子的每个价轨道和每个内层轨道各用一个$TO代表的基组,例如碳原子的极小 基组是中1.(5.6727)、中2(1.6083)八、中2(1.2107)、中2(1.2107)、中2(1.2107).其中括号内数字为值.极小基 组的计算结果可给出分子的正确几何构型,定性地研究分子的性质,用极小基组一般不能得出有定量意义 的结果 (2)双(基组:每个原子轨道用两卟不同的STO代表的基组,它比极小基组大了一倍,可大为改善极 小基组的SCF计算结果. (3)扩展基组:任何大于双(基组的基组,扩展基组中一最重要的是加“极化函数”的基组.极化函数是 指角量子数比价轨道角量子数大1或2的STO.例如,第二周期原子的极化函数是5个3dSTO.极化函数 的作用是能描述在形成分子过程中原子轨道的变型,可给出相当精确的SC℉计算结果. 对于非线性多原子分子的计算,若采用STO基组,则(5-14)式中的双电子积分(vWo)和(vo)中含有大 量的三中心和四中心积分,对这些多中心积分的计算比较困难,一般STO基组只用来计算双原子分子或线 型分子. 2)Gauss函数基组 对于多原子分子的计算,为了避免计算多中心积分的困难,常用Guss函数基组(GTO).在直角坐标系 中,以A为中心的广义Gauss函数定义为 GA-NxAymzre-arA (5-20) 式中N为归一化常数,a为参数,而且 N=29 (4a)l+m+n 72 π (2l+1)(2m+1)(2n-1) (5-21) rA2=x42+y42+2 (5-22) Gauss函数有一个重要性质:两个不同中心的Gauss函数的乘积,可用另一个中心的Gauss函数的线性组合 来表示.因此,以Guss函数作为基组,可把计算多中心积分简化为计算单中心积分,从而解决了计算多 中心积分的函数.但Gauss函数不如Slater函数符合实际的原子轨道,为克服Gauss函数的这一缺点,常用 多个GTO的线性组合来拟合STO.这种用GTO线性组合而形成的基组称为简缩Gauss基组(contracted gaussian type orbitals,CGTO). 一组常用的方法是用k个GTO的线性组合逼近一个STO,这种基组称为STO-kG基组,例如STO-3G, STO-4G等.对于一般的应用,STO-4G的精确度就可以了. 比STO-kG更好一些的基组是所谓“分裂价基”,其中每个内层轨道用一个STO-kG逼近,而每个价轨道 127
127 子的键长和键角,即确定分子的几何构型;对于化学反应的研究,可以计算由反应物向产物转变过程中各 原子坐标不同位置的总能量,并得到总能量曲面(习惯上称为势能面),由这张曲面可以了解反应路径,活 化能、过渡态等信息. 5.1.3 基函数的选择 基函数组(简称基组)是分子轨道展开的基础,基组选择的好坏对于 SCF 计算结果至关重要,为了得 到精确的计算结果,一般需要选择较大的基组.若基函数的数目为 N,则计算量与 N 4 成正比.在实际计算 中,常根据需要来确定基组,不能一味追求精确度而招致过大的计算量.现在,最常用的是 Slater 函数基组 和 Gauss 函数基组. 1)Slater 函数基组 Slater 函数基组即 Slater 型轨道(STO)[见(2-79)式]。 ϕn l m=Nsr n-1 e -ζr Yl m(θ,φ) (5-18) 式中 Ns 为归一化常数 Ns=(2ζ) (2n+1)/2/√2݊! (5-19) ζ 为轨道指数,可用 Slater 函数作原子的 SCF 计算,根据使总能量最低的原则确定各原子轨道的 ζ.n,l,m 对 应于原子轨道的三个量子数.Slater 基组可分为下列几种: (1)极小基组:分子中原子的每个价轨道和每个内层轨道各用一个 STO 代表的基组,例如碳原子的极小 基组是 ϕ1s(5.6727)、ϕ2s(1.6083)、ϕ2px(1.2107)、ϕ2py (1. 2107)、ϕ2pz(1.2107).其中括号内数字为 ζ 值.极小基 组的计算结果可给出分子的正确几何构型,定性地研究分子的性质,用极小基组一般不能得出有定量意义 的结果. (2)双 ζ 基组:每个原子轨道用两卟不同 ζ 的 STO 代表的基组,它比极小基组大了一倍,可大为改善极 小基组的 SCF 计算结果. (3)扩展基组:任何大于双 ζ 基组的基组,扩展基组中一最重要的是加“极化函数”的基组.极化函数是 指角量子数比价轨道角量子数大 1 或 2 的 STO.例如,第二周期原子的极化函数是 5 个 3d STO.极化函数 的作用是能描述在形成分子过程中原子轨道的变型,可给出相当精确的 SCF 计算结果. 对于非线性多原子分子的计算,若采用 STO 基组,则(5-14)式中的双电子积分(vμ|λσ)和(vσ|λμ)中含有大 量的三中心和四中心积分,对这些多中心积分的计算比较困难,一般 STO 基组只用来计算双原子分子或线 型分子. 2) Gauss 函数基组 对于多原子分子的计算,为了避免计算多中心积分的困难,常用 Gauss 函数基组(GTO).在直角坐标系 中,以 A 为中心的广义 Gauss 函数定义为 GA=Nݔ ݕ ݖ eିమ (5-20) 式中 N 为归一化常数,a 为参数,而且 N=( ଶ గ ) 3/4[ ሺସሻశశ ሺଶାଵሻ‼ሺଶାଵሻ‼ሺଶିଵሻ‼ ] 1/2 (5-21) rA 2 =xA 2 +yA 2 +zA 2 (5-22) Gauss 函数有一个重要性质:两个不同中心的 Gauss 函数的乘积,可用另一个中心的 Gauss 函数的线性组合 来表示.因此,以 Gauss 函数作为基组,可把计算多中心积分简化为计算单中心积分,从而解决了计算多 中心积分的函数.但 Gauss 函数不如 Slater 函数符合实际的原子轨道,为克服 Gauss 函数的这一缺点,常用 多个 GTO 的线性组合来拟合 STO.这种用 GTO 线性组合而形成的基组称为简缩 Gauss 基组(contracted gaussian type orbitals,CGTO). 一组常用的方法是用 k 个 GTO 的线性组合逼近一个 STO,这种基组称为 STO-kG 基组,例如 STO-3G, STO-4G 等.对于一般的应用,STO-4G 的精确度就可以了. 比 STO-kG 更好一些的基组是所谓“分裂价基”,其中每个内层轨道用一个 STO-kG 逼近,而每个价轨道

用两个STO-kG逼近.这是考虑到形成分子时,原子的内层轨道变化较小,而价轨道变化较大,常用的这 类基组是4-31G基组,它是用一个STO-4G逼近内层轨道,用一个STO-3G和一个STO-1G逼近价轨道. 更精确的基组是双C型的简缩Guss基组,即每个轨道用两个STO-kG逼近,其中内层轨道取较大的K 值,以逼近歧点的性质,外层轨道取较小的k值,这种双C型简缩Guss基组,可在总的GTO数目增加不 多的情况下,使计算结果有较大的改进】 5.2分子轨道的近似计算方法 从头计算法是一种精确的计算方法,其缺点是计算量大,以致在计算机条件不完备的情况下,其应用 范围受到了限制,人们不得不寻找一些分子轨道的近似计算方法,或称为半经验的分子轨道方法,借助经 验参数来简化从头计算,分子轨道的近似计算方法有很多种,对这些方法的详细讨论远远超出了本书的范 围,在这里只介绍其中常用的两种:CNDO法和EHMO法. 5.2.1CND0法 在LCAO自治场分子轨道的计算中,计算量最大的是对大量的双电子排斥积分(5-13)式的计算,其实许 多这类双电子积分的数值接近于零,特别是那些包含v的微分重迭中*(I)冲(I)1,忽略这些数值非常小 的微分重迭,保留电子间排斥的主要特征的基本理论是Pople,,Santry和Segal引进的CNDO法(complete neglect of diffcrential overlap method,.即全略微分重迭法). CDO法只处理价电子.把内层电子和原子核合在一起作为原子实.于是,原子轨道基集合是一个价 基集合,例如,对于碳原子为2s,2px,2p,2p 和从头计算法一样,CNDO法也须解Roothaan方程(5-11),只是在解方程的过程中采用了大量的近似. 在分子轨道的归一化中,忽略相应的重迭积分 Sm=中u*(1)冲,(1)dy1=6un (5-23) 对双电子排斥积分采用较强的近似,令(5-13)式 (HavelApOd)-YabOacObaourOxa (5-24) 式中下标a,c,c,d表示该原子轨道所属于的原子,在这个近似下,忽略了全部的三中心和四中心双电子 积分,只保留了双中心积分和单中心积分 (HaLlalAbAb)-Yab (5-25) (uadl入a入a)-Yaa (5-26) 而且Yab和yaa只与原子的本质有关,并不依赖于轨道u和入的实际类型,其中yab和yaa或用小的基组计算 或用经验参数代替. 在CNDO法中,对矩阵元 h=∫p,*(I)A1中(I)dv 也采用了近似,在价电子近似下,包括了核与内层电子的贡献 huv-BabSu (5-27) 式中S为重迭积分;Bb为成键参量,用经验参数代替. CNDO法可用于计算分子的几何构型,电荷分布、能级等,是一种常用的半经验计算方法. 5.2.2EHMO法 EHMO(extended Huckel molecular orbital)法,或称推广的Huckel法,是另一种应用较为广泛的半经验 128
128 用两个 STO-kG 逼近.这是考虑到形成分子时,原子的内层轨道变化较小,而价轨道变化较大,常用的这 类基组是 4-31G 基组,它是用一个 STO-4G 逼近内层轨道,用一个 STO-3G 和一个 STO-1G 逼近价轨道. 更精确的基组是双 ζ 型的简缩 Gauss 基组,即每个轨道用两个 STO-kG 逼近,其中内层轨道取较大的 k 值,以逼近歧点的性质,外层轨道取较小的 k 值,这种双 ζ 型简缩 Gauss 基组,可在总的 GTO 数目增加不 多的情况下,使计算结果有较大的改进. 5.2 分子轨道的近似计算方法 从头计算法是一种精确的计算方法,其缺点是计算量大,以致在计算机条件不完备的情况下,其应用 范围受到了限制,人们不得不寻找一些分子轨道的近似计算方法,或称为半经验的分子轨道方法,借助经 验参数来简化从头计算,分子轨道的近似计算方法有很多种,对这些方法的详细讨论远远超出了本书的范 围,在这里只介绍其中常用的两种:CNDO 法和 EHMO 法. 5.2.1 CNDO 法 在 LCAO 自治场分子轨道的计算中,计算量最大的是对大量的双电子排斥积分(5-13)式的计算,其实许 多这类双电子积分的数值接近于零,特别是那些包含 μ≠v 的微分重迭 ϕμ*(1)ϕv(1)dv1,忽略这些数值非常小 的微分重迭,保留电子间排斥的主要特征的基本理论是 Pople,Santry 和 Segal 引进的 CNDO 法(complete neglect of diffcrential overlap method,即全略微分重迭法). CNDO 法只处理价电子.把内层电子和原子核合在一起作为原子实.于是,原子轨道基集合是一个价 基集合,例如,对于碳原子为 2s,2px,2py,2pz. 和从头计算法一样,CNDO 法也须解 Roothaan 方程(5-11),只是在解方程的过程中采用了大量的近似. 在分子轨道的归一化中,忽略相应的重迭积分 Sμv=∫ϕμ*(1)ϕv(1)dv1=δμv (5-23) 对双电子排斥积分采用较强的近似,令(5-13)式 (μavc|λbσd)=γabδacδbdδμvδλσ (5-24) 式中下标 a,c,c,d 表示该原子轨道所属于的原子,在这个近似下,忽略了全部的三中心和四中心双电子 积分,只保留了双中心积分和单中心积分 (μaμa|λbλb)=γab (5-25) (μaμa|λaλa)=γaa (5-26) 而且 γab 和 γaa 只与原子的本质有关,并不依赖于轨道 μ 和 λ 的实际类型,其中 γab和 γaa或用小的基组计算 或用经验参数代替. 在 CNDO 法中,对矩阵元 hvμ=∫ϕv*(1)ܪଵϕμ(1)dv1 也采用了近似,在价电子近似下,ܪଵ包括了核与内层电子的贡献. ߚ=hμv Svμ (5-27) 式中 Svμ为重迭积分;ߚ 为成键参量,用经验参数代替. CNDO 法可用于计算分子的几何构型,电荷分布、能级等,是一种常用的半经验计算方法. 5.2.2 EHMO 法 EHMO (extended Huckel molecular orbital)法,或称推广的 Huckel 法,是另一种应用较为广泛的半经验

分子轨道法.EHMO法与CNDO法一样,只处理价电子,即也采用价电子近似,与CNDO法不同的是, EHMO法不明确定义单电子的Hamilton算符(I),所以(5-9)式的Fu就没有明确的表达式,而由经验参数 确定。 虽然在形式上EHMO法也是解Roothaan方程(5-l1),但由于Fu没有明确的表达式,所以并不处理双 电子积分(5-13)式,在这个意义上,EHMO法是一种单电子理论,而CNDO法则是双电子理论 在EHMO法中,矩阵元F用原子轨道中,上电子电离势的负值来近似,即 Fm=中,*(I)F(1)Φ(1)dv-l (5-28) 例如,对于氢原子轨道中1s,则F1ls可取为-13.6eV;对于碳原子轨道2p,则F2p2p可取为-11.4eV,而 Fvu-0.5k(F+Fuu)Syu (5-29) 其中k为经验参数,取值范围是1一3:重迭积分Su可由选定能原子轨道和核间距直接计算出来 用这种经验的方法所确定的,显然并不含有待计算的原子轨道组合系数c,所以用EHMO法解Roothaan 方程(5-11)可以不用SCF方法计算.一般直接求解方程(5-11)所对应的久期方程 detFu-E Syu=0 (5-30) 式中左边的符号表示行列式.由上式可解出∈,将E,代回到方程(5-11)可确定c 由于EHMO法的F(I)没有明确定义,且Fu直接取自电于的电离势,所以体系价电于的总能量E,a1可 表示为各个价电子能量之和: Ea=∑e (5-31) 在一般的分子轨道法中,须明确考虑双电子积分,在这种情况下,总能量不等于各个电子能量之和:因电 子间排斥能被计算两次,所以总能量为各单电子能量之和再减掉电子间总排斥能. EHMO法看起来很粗糙,但由于其矩阵元的数值直接取自实验数据,因而增加了计算结果的可靠 性.EHMO法的优点是计算量小,可用来计算较为复杂的体系,特别是含有重原子的体系.EHMO法可用 来计算分子轨道的能级顺序,分于的电荷分布,分子的几何构型等参数,对于低极性分子,EHMO法的计 算结果尚比较可靠, 5.3 Huckel分子轨道法 Huckel分子轨道法简称为HMO法.这一方法是用来定性地处理含有大π键的简单共轭分子,把共轭 分子的诸原子核、内层电子以及σ键上的电子看成是分子实,而只处理π电子,下面以丁二烯分子为例来 讨论HMO方法. 5.3.1 Huckel近似 有机共轭分子,如丁二烯,是平面分子.其中每个碳原子的 2s,2px,2p,轨道采用sp2杂化,形成C-H和C-Co键,余下的 四个C原子的2p轨道互相平行,且每个2P.轨道上有一个电子, 这些2p:轨道可以互相重选而形成π型分子轨道.图5.1是丁二烯 分子σ键和2p轨道的示意图,容易看出,丁二烯的0型原子轨道 2s,2p,2p,对于分子平面(xy平面)的反映是对称的,而π型原子 轨道2:对该平面的反映则是反对称的,这两种类型的轨道由于对 图5.1丁二烯分子的σ键和2p.轨道 称性不匹配,所以不能有效地形成分子轨道,这样就可以把这两类 原子轨道分开处理:碳的2s,2px,2p,和氢的1s轨道相互组合成ō型分子轨道,可由前两节讨论的各种分 子轨道方法计算其组合系数和轨道能量,这里不再讨论,碳的2:轨道也可相互组合而形成π型分子轨道(也 可以用较精确的分子轨道法计算π型分子轨道及其轨道能量),下面我们介绍用HMO法对丁二烯π型分子 129
129 分子轨道法.EHMO 法与 CNDO 法一样,只处理价电子,即也采用价电子近似,与 CNDO 法不同的是, EHMO 法不明确定义单电子的 Hamilton 算符ܨ (1),所以(5-9)式的 Fvμ就没有明确的表达式,而由经验参数 确定。 虽然在形式上 EHMO 法也是解 Roothaan 方程(5-11),但由于 Fvμ 没有明确的表达式,所以并不处理双 电子积分(5-13)式,在这个意义上,EHMO 法是一种单电子理论,而 CNDO 法则是双电子理论. 在 EHMO 法中,矩阵元 Fvv用原子轨道 ϕv上电子电离势的负值来近似,即 Fvv=∫ϕv*(1)ܨ (1)ϕv(1)dv1≈െIv (5-28) 例如,对于氢原子轨道 ϕ1s,则 F1s1s可取为െ13.6eV;对于碳原子轨道 ϕ2p,则 F2p2p 可取为െ11.4 eV.而 Fvμ=0.5k(Fvv+Fμμ)Svμ (5-29) 其中 k 为经验参数,取值范围是 1—3;重迭积分 Svμ可由选定能原子轨道和核间距直接计算出来. 用这种经验的方法所确定的,显然并不含有待计算的原子轨道组合系数cμi,所以用EHMO法解Roothaan 方程(5-11)可以不用 SCF 方法计算.一般直接求解方程(5-11)所对应的久期方程 det|Fvμെ∈iSvμ|=0 (5-30) 式中左边的符号表示行列式.由上式可解出∈i,将∈i 代回到方程(5-11)可确定 cμi. 由于 EHMO 法的ܨ (1)没有明确定义,且 Fvμ直接取自电于的电离势,所以体系价电于的总能量 Ev a l 可 表示为各个价电子能量之和: Eval= i ∈i (5-31) 在一般的分子轨道法中,须明确考虑双电子积分,在这种情况下,总能量不等于各个电子能量之和:因电 子间排斥能被计算两次,所以总能量为各单电子能量之和再减掉电子间总排斥能. EHMO 法看起来很粗糙,但由于其矩阵元的数值直接取自实验数据,因而增加了计算结果的可靠 性.EHMO 法的优点是计算量小,可用来计算较为复杂的体系,特别是含有重原子的体系.EHMO 法可用 来计算分子轨道的能级顺序,分于的电荷分布,分子的几何构型等参数,对于低极性分子,EHMO 法的计 算结果尚比较可靠. 5.3 Huckel 分子轨道法 Huckel 分子轨道法简称为 HMO 法.这一方法是用来定性地处理含有大 π 键的简单共轭分子,把共轭 分子的诸原子核、内层电子以及 σ 键上的电子看成是分子实,而只处理 π 电子,下面以丁二烯分子为例来 讨论 HMO 方法. 5.3.1 Huckel 近似 有机共轭分子,如丁二烯,是平面分子.其中每个碳原子的 2s,2px,2py轨道采用 sp 2杂化,形成 CെH 和 CെC σ 键,余下的 四个 C 原子的 2pz 轨道互相平行,且每个 2pz轨道上有一个电子, 这些 2pz 轨道可以互相重选而形成 π 型分子轨道.图 5.1 是丁二烯 分子 σ 键和 2pz 轨道的示意图,容易看出,丁二烯的 σ 型原子轨道 2s,2px,2py对于分子平面(xy 平面)的反映是对称的,而 π 型原子 轨道 2pz 对该平面的反映则是反对称的,这两种类型的轨道由于对 称性不匹配,所以不能有效地形成分子轨道,这样就可以把这两类 原子轨道分开处理:碳的 2s,2px,2py和氢的 1s 轨道相互组合成 σ 型分子轨道,可由前两节讨论的各种分 子轨道方法计算其组合系数和轨道能量,这里不再讨论,碳的 2pz 轨道也可相互组合而形成 π 型分子轨道(也 可以用较精确的分子轨道法计算 π 型分子轨道及其轨道能量),下面我们介绍用 HMO 法对丁二烯 π 型分子 图 5.1 丁二烯分子的 σ 键和 2pz 轨道 C C C C 2pz 2pz 2pz 2pz

轨道的处理. 丁二烯中四个碳原子的每一个2印:电子(称为π电子)在诸原子核和其它电子的势场中运动,其单电子 的Hamilton算符记为h,π电子的分子轨道记为,则π电子的单电子Schrodinger方程为 hψ,=eψ: (5-32) 在HMO方法中,没有明确定义。∈和中,可由线性变分法确定,即,用四个2p-原子轨道的线性组合表示 ,Fc1中+c2中2+c3中p3+c4中4 (5-33) 其中1,2,中3,4分别为四个2p轨道,按变分法,应先写出E,的表达式: 44 ∑∑cmcnomhondi地 ∫ph:dvmn台 E= (5-34) ∫dv 44 ∑∑cmcnsΦnDndv m=l n=l 在Huckel方法中采用Huckel近似: (1)令 Hnmm=∫中nh中nmdh=a (5-35) 式中为碳原子2p:电子的平均能量,与碳原子的位置无关,可由实验确定.a称为Coulomb积分 (2)令 Hnm=∫中ni中ndh= 0m,n不相邻 (5-36) B m,n相邻 式中B为交换积分,所有相邻原子的2间的交换积分都为B,B也可由实验确定.B的值决定了相邻原子π 键的强度 (3)令 0 S∫中中d=nBm=n m≠n (5-37) 即略去所有原子间的重迭,且每个2轨道都是归一化的. 5.3.2丁二烯HMO久期方程的解 在Huckel近似下,可得到e,的表达式 (c子+c吃+c学+c)a+2(c1c2+c2c3+c3c4)B (5-38) (c+c陉+c子+c) 为了求出E,的极小值,须计算 dEi dEi dei dei (5-39) 0C1 0C2 0C3 0C4 把(5-38)式的∈,表达式代入上式,得c1,c2,3,c4所应满足的方程: (a-e)c1+Bc2=0Bc1+(ar-E)c2+Bc3=0Bc2+(a-E)c3+Bc4=0Bc3+(a-e)c4=0(5-40) 由该方程组所解出的c1,c2,c3,c4即为E,取极小值的组合系数.这是一个线性齐次方程组,该方程组有非 零解的条件是其系数行列式等于零 a-Ei B 0 0 a-Ei 0 0 B a-Ei B =0 (5-41) 0 0 a-Ei 这就是丁二烯的HMO久期方程.为方便计,令 Q-Ei x= (5-42) B |x1001 则久期方程为 1 x 1 0 =0 0 1 x 1 (5-43) 10 01 x 130
130 轨道的处理. 丁二烯中四个碳原子的每一个 2pz 电子(称为 π 电子)在诸原子核和其它电子的势场中运动,其单电子 的 Hamilton 算符记为݄,π 电子的分子轨道记为 ψi,则 π 电子的单电子 Schrödinger 方程为 ݄ψi=∈iψi (5-32) 在 HMO 方法中.݄没有明确定义。∈i 和 ψi 可由线性变分法确定,即 ψi 用四个 2pz 原子轨道的线性组合表示 ψi=c1ϕ1+c2ϕ2+c3ϕ3+c4ϕ4 (5-33) 其 ϕ1,ϕ2,ϕ3,ϕ4 分别为四个 2pz 轨道,按变分法,应先写出∈i 的表达式: ∈i= టటୢ௩ ట మୢ௩ = 4 1 4 1 m n థథௗ௩ 4 1 4 1 m n థథௗ௩ (5-34) 在 Huckel 方法中采用 Huckel 近似: (1)令 Hmm=∫ϕm݄ϕmdv=α (5-35) 式中 α 为碳原子 2pz 电子的平均能量,与碳原子的位置无关,可由实验确定.α 称为 Coulomb 积分. (2)令 Hmn=∫ϕm݄ϕndv= ቊ0 ݉,݊不相邻 ߚ݊,݉ 相邻 (5-36) 式中 β 为交换积分,所有相邻原子的 2pz 间的交换积分都为 β,β 也可由实验确定.β 的值决定了相邻原子 π 键的强度. (3)令 S=∫ϕmϕndv=n ൜0 ݉ ് ݊ ߚ݉ ൌ݊ (5-37) 即略去所有原子间的重迭,且每个 2pz 轨道都是归一化的. 5.3.2 丁二烯 HMO 久期方程的解 在 Huckel 近似下,可得到∈i 的表达式 ∈i= ൫భ మାమ మାయ మାర మ൯ఈାଶሺభమାమయାయరሻఉ ൫భ మାమ మାయ మାర మ൯ (5-38) 为了求出∈i 的极小值,须计算 డ∈ డభ = డ∈ డమ = డ∈ డయ = డ∈ డర (5-39) 把(5-38)式的∈i 表达式代入上式,得 c1,c2,c3,c4所应满足的方程: (αെ∈i)c1+βc2=0 βc1+(αെ∈i)c2+βc3=0 βc2+(αെ∈i)c3+βc4=0 βc3+(αെ∈i)c4=0 (5-40) 由该方程组所解出的 c1,c2,c3,c4即为∈i 取极小值的组合系数.这是一个线性齐次方程组,该方程组有非 零解的条件是其系数行列式等于零 ተ 00ߚ ∋െ ߙ 0 ߚ ∋െ ߙ ߚ ߚ ∋െ ߙ ߚ 0 0 0 ߚ ߙ െ∈ ተ=0 (5-41) 这就是丁二烯的 HMO 久期方程.为方便计,令 x= ఈି∈ ఉ (5-42) 则久期方程为 ተ 100ݔ 1ݔ10 01ݔ1 001ݔተ=0 (5-43)

可把久期方程的这种形式推广到一般的链共轭多烯,含有n个碳原子的链共轭多烯,其久期方程为n 阶行列式等于零,其中行列式中主对角线上的元素为x,与主对角线上的元素相邻的元素为1,其余元素为 零,记住这个规则对用HMO法解链共轭多烯问题是方便的。 方程(5-43)可化为双二次方程: x4+3x2+1=0 解之得 x=1.618,2=0.618,x3=-0.618,x4=-1.618 由(5-42)式得 ∈1=+1.618β∈2=+0.618β∈3=-0.618B∈4=a-1.618B (5-44) 把∈1,∈2,∈3,∈4分别代回到方程组(5-40),并利用归一化条件 Jlpd=c12+c22+c2+c42=1 (5-45) 对应于每个能量E,,可得到一组系数C1,c2,c3,c4,由这组系数可得到中,对应于∈1,∈2,E3,∈4的四个 π型分子轨道分别为 =0.3717中1+0.60152+0.60153+0.3717φ4ψ2=0.6015中1+0.3717φ2-0.3717φ3-0.6015φ4 3=0.60151-0.3717中2-0.3717中3+0.60154ψ4=0.3717中1-0.60152+0.6015中3-0.3717中4 (5-46) 交换积分B值总是负的,四个π轨道的能级图如图5.2所示,图中箭头表示电子的自旋方向. -E, ↑年牛牛 2p: e 图5.2丁二烯π轨道的能级图和电子排布 图5.3是丁二烯的四个2.轨道图形及其所形成的四个π分子轨道图形.图中的虚线表示节面, 8888 888888888888 1 2 名 图5.3丁二烯的2p轨道和π分子轨道 从分子轨道的观点看来,化学反应必然涉及到电子运动状态的变化.在分子中,每个电子的状态都是 用分子轨道来描述的,电子状态的变化意味着电子从一个轨道转移到另一个轨道,对于分子的各个占据轨 道的电子,其中最高占据轨道HOMO)上的电子能量最高,最活跃,因而最容易转移到其它分子的最低空轨 道(LUMO)上,这就是说,化学反应所涉及到的分子轨道往往是最高占据轨道和最低空轨道,这两种轨道统 称为前线轨道(FMO). 5.3.3离域能 图5.3表明,丁二烯的四个π电子不是只定域在两个特定的碳原子之间,而是非定域地运动在整个分子 的碳骨架上,这样的化学键为离域π键或大π键.由(5-44)式和图5.2可以算出这四个π电子的总能量EDm: EDm=4a+4.472B (5-47) 如果假定丁二烯中的两对π电子分别定域在1和2碳原子之间以及3和4碳原子之间,即假定形成两个小π 键:C=C-C=C.这时2和3碳原子间不形成丌键,所以B23=B2=0,久期方程(5-43)变为 131
131 可把久期方程的这种形式推广到一般的链共轭多烯,含有 n 个碳原子的链共轭多烯,其久期方程为 n 阶行列式等于零,其中行列式中主对角线上的元素为 x,与主对角线上的元素相邻的元素为 1,其余元素为 零,记住这个规则对用 HMO 法解链共轭多烯问题是方便的。 方程(5-43)可化为双二次方程: x 4 +3x 2 +1=0 解之得 xl=1.618,x2=0.618,x3=െ0.618,x4=െ1.618 由(5-42)式得 ∈1=α+1.618β ∈2=α+0.618β ∈3=αെ0.618β ∈4=αെ1.618β (5-44) 把∈1,∈2,∈3,∈4 分别代回到方程组(5-40),并利用归一化条件 ∫|ψi| 2 dv=c1 2 +c2 2 +c3 2 +c4 2 =1 (5-45) 对应于每个能量∈i,,可得到一组系数 c1,c2,c3,c4,由这组系数可得到 ψi,对应于∈1,∈2,∈3,∈4 的四个 π 型分子轨道分别为 ψ1=0.3717ϕ1+0.6015ϕ2+0.6015ϕ3+0.3717ϕ4 ψ2=0.6015ϕ1+0.3717ϕ2െ0.3717ϕ3െ0.6015ϕ4 ψ3=0.6015ϕ1െ0.3717ϕ2െ0.3717ϕ3+0.6015ϕ4 ψ4=0.3717ϕ1െ0.6015ϕ2+0.6015ϕ3െ0.3717ϕ4 (5-46) 交换积分 β 值总是负的,四个 π 轨道的能级图如图 5.2 所示,图中箭头表示电子的自旋方向. ∈1 ∈2 ↑ ↑ ↑ ↑ 2pz ↑↓ ∈3 ↑↓ ∈4 图 5.2 丁二烯 π 轨道的能级图和电子排布 图 5.3 是丁二烯的四个 2pz轨道图形及其所形成的四个 π 分子轨道图形.图中的虚线表示节面. ψ1 ψ2 ψ3 ψ4 图 5.3 丁二烯的 2pz 轨道和 π 分子轨道 从分子轨道的观点看来,化学反应必然涉及到电子运动状态的变化.在分子中,每个电子的状态都是 用分子轨道来描述的,电子状态的变化意味着电子从一个轨道转移到另一个轨道,对于分子的各个占据轨 道的电子,其中最高占据轨道(HOMO)上的电子能量最高,最活跃,因而最容易转移到其它分子的最低空轨 道(LUMO)上.这就是说,化学反应所涉及到的分子轨道往往是最高占据轨道和最低空轨道,这两种轨道统 称为前线轨道(FMO). 5.3.3 离域能 图 5.3 表明,丁二烯的四个 π 电子不是只定域在两个特定的碳原子之间,而是非定域地运动在整个分子 的碳骨架上,这样的化学键为离域 π 键或大 π 键.由(5-44)式和图 5.2 可以算出这四个 π 电子的总能量 EDπ: EDπ=4α+4.472β (5-47) 如果假定丁二烯中的两对 π 电子分别定域在 1 和 2 碳原子之间以及 3 和 4 碳原子之间,即假定形成两个小 π 键:C=CെC=C.这时 2 和 3 碳原子间不形成丌键,所以 β23=β32=0,久期方程(5-43)变为

10 01 1 x 0 0 =0 0 (5-48) 100 1 x 解之得,由一得 E=E2=a+B E3=E4=-B (5-49) B 其能级如图5.4所示,这时四个定域π电子的总能量为Em: ELn-4a+4 (5-50) a+B 2p: ””“”女1””“下个 2pa a-β 图5.4丁二烯定域π轨道的能级 共轭分子的离域能(或称为共轭能,记为DEπ)定义为 DEx-ELn-EDn (5-51) 对于丁二烯分子,其离域能为 DE=-0.472β (5-52) 其中πO,即丁二烯形成大π键比形成两个小π键具有更低的能量,形成大π键就更稳定. 由于丁二烯中存在这种共轭效应,所以欲使丁二烯离解就比较困难,从而可以解释丁二烯具有较高的 热稳定性.另一方面,丁二烯的HOMO比乙烯的高,放容易失去电子:丁二烯的LUMO比乙烯的低,故 容易接受外来电子,由此可以解释丁二烯的加成活性和π络合活性均比乙烯高. 虽然可以用HMO方法的计算结果定性解释一些共轭分子的化学性质,但HMO方法毕竞是很粗糙的近 似方法,不能指望用HMO的计算结果解释各种化学现象.当HMO方法不能胜任的时候,应该应用其它更 精确的计算方法. 5.4 HMO方法的应用 5.4.1链共轭多烯和单环平面共轭多烯 这类分子的π电子成键问题,也可用HMO方法作定性讨论.设π型分子轨道中由π型原子轨道中, 线性组合而成: ∑c中, (5-53) 对于含有n个碳原子的链共轭多烯 CH2=[CH-CH=1/2-1CH2 可以仿照丁二烯的HMO处理方法,解由n阶行列式构成的久期 jπ 方程,可得到轨道能量为 ∈F+2fcos +1l,2,,n (5-54) 组合系数为 sn+1方l,2,,n (5-55) 含有n个碳原子的单环平面共轭多烯CmH,例如苯分子C6H6,可用上节介绍的方法直接写出其久期方程 1x10001 1 x1000 0 1x100 0 1x1 =0 0 (5-56) 0 01x1 1000 132
132 ተ 100ݔ 1ݔ00 00ݔ1 001ݔተ=0 (5-48) 解之得 x=±l,由 x= ఈି∈ ఉ 得 ∈l=∈2=α+β ∈3=∈4=αെβ (5-49) 其能级如图 5.4 所示,这时四个定域 π 电子的总能量为 ELπ: ELπ=4α+4 (5-50) α+β ↑ ↑ ↑ ↑ 2pz ↑↓ ↑↓ 2pz α-β 图 5.4 丁二烯定域 π 轨道的能级 共轭分子的离域能(或称为共轭能,记为 DEπ)定义为 DEπ=ELπെEDπ (5-51) 对于丁二烯分子,其离域能为 DEπ=െ0.472β (5-52) 其中 π0,即丁二烯形成大 π 键比形成两个小 π 键具有更低的能量,形成大 π 键就更稳定. 由于丁二烯中存在这种共轭效应,所以欲使丁二烯离解就比较困难,从而可以解释丁二烯具有较高的 热稳定性.另一方面,丁二烯的 HOMO 比乙烯的高,放容易失去电子;丁二烯的 LUMO 比乙烯的低,故 容易接受外来电子,由此可以解释丁二烯的加成活性和 π 络合活性均比乙烯高. 虽然可以用 HMO 方法的计算结果定性解释一些共轭分子的化学性质,但 HMO 方法毕竟是很粗糙的近 似方法,不能指望用 HMO 的计算结果解释各种化学现象.当 HMO 方法不能胜任的时候,应该应用其它更 精确的计算方法. 5.4 HMO 方法的应用 5.4.1 链共轭多烯和单环平面共轭多烯 这类分子的 π 电子成键问题,也可用 HMO 方法作定性讨论.设 π 型分子轨道 ψj 由 π 型原子轨道 ϕr 线性组合而成: ψj= r cjrϕr (5-53) 对于含有 n 个碳原子的链共轭多烯 CH2=[CHെCH=]n/2-1CH2 可以仿照丁二烯的 HMO 处理方法,解由 n 阶行列式构成的久期 方程,可得到轨道能量为 ∈j=α+2βcos గ ାଵ,j=1, 2, …, n (5-54) 组合系数为 cjr=( ଶ ାଵ) 1/2sin గ ାଵ,j, r=1, 2, …, n (5-55) 含有 n 个碳原子的单环平面共轭多烯 CnHn,例如苯分子 C6H6,可用上节介绍的方法直接写出其久期方程 ተ ተ 10001ݔ 1ݔ1000 01ݔ100 001ݔ10 0001ݔ1 ݔ10001 ተ ተ =0 (5-56)
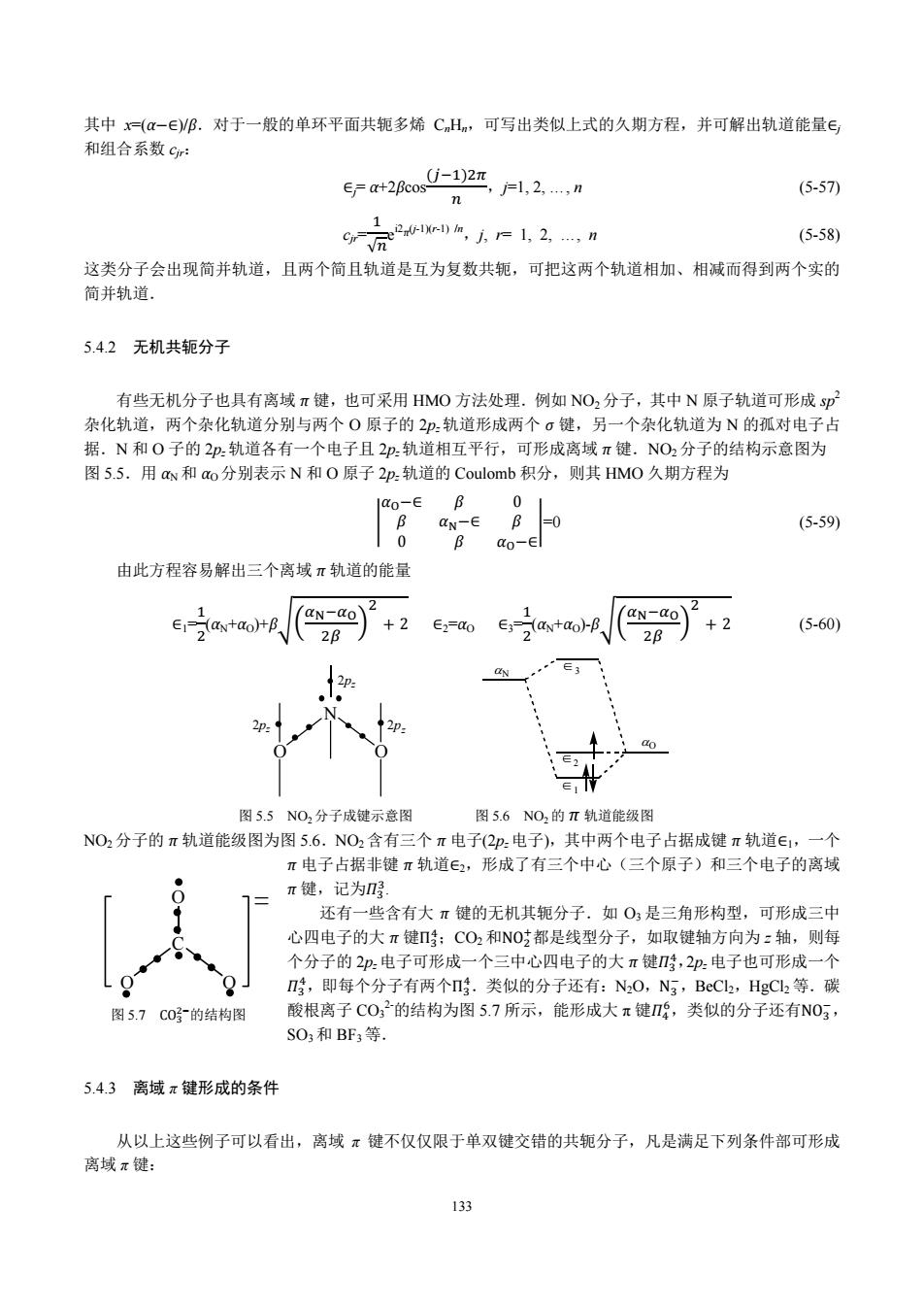
其中x=(a-∈)B.对于一般的单环平面共轭多烯CmH,可写出类似上式的久期方程,并可解出轨道能量∈ 和组合系数cr: ∈=a+2fcos j-1)2π =1,2,…,n (5-57) =2m,方,=1,2,,n c in (5-58) 这类分子会出现简并轨道,且两个简且轨道是互为复数共轭,可把这两个轨道相加、相减而得到两个实的 简并轨道. 5.4.2无机共轭分子 有些无机分子也具有离域π键,也可采用HMO方法处理.例如NO2分子,其中N原子轨道可形成sp 杂化轨道,两个杂化轨道分别与两个O原子的2.轨道形成两个σ键,另一个杂化轨道为N的孤对电子占 据.N和O子的2p轨道各有一个电子且2轨道相互平行,可形成离域π键.NO2分子的结构示意图为 图5.5.用aw和ao分别表示N和O原子2p.轨道的Coulomb积分,则其HMO久期方程为 Qo-E B 0 B aN-E (5-59) 0 B o-∈l 由此方程容易解出三个离域π轨道的能量 2 aN-dO +2 E3->(ax+ao)-B aN-QO ∈12 +B、 +2 2B 2B (5-60) N 图5.5NO,分子成键示意图 图5.6NO,的π轨道能级图 NO2分子的π轨道能级图为图5.6.NO2含有三个π电子(2p:电子),其中两个电子占据成键π轨道∈1,一个 π电子占据非键π轨道E2,形成了有三个中心(三个原子)和三个电子的离域 π键,记为 还有一些含有大π键的无机其轭分子.如O,是三角形构型,可形成三中 心四电子的大π键n;CO2和NO都是线型分子,如取键轴方向为:轴,则每 个分子的2p.电子可形成一个三中心四电子的大π键,2p.电子也可形成一个 ,即每个分子有两个.类似的分子还有:N2O,N3,BeCl2,HgC2等.碳 图5.7C0号的结构图 酸根离子CO32的结构为图5.7所示,能形成大π键Π,类似的分子还有N03, SO3和BF3等. 5.4.3离域π键形成的条件 从以上这些例子可以看出,离域π键不仅仅限于单双键交错的共轭分子,凡是满足下列条件部可形成 离域π键: 133
133 其中 x=(αെ∈)/β.对于一般的单环平面共轭多烯 CnHn,可写出类似上式的久期方程,并可解出轨道能量∈j 和组合系数 cjr: ∈j= α+2βcos ሺିଵሻଶగ ,j=1, 2, …, n (5-57) cjr= ଵ √ e i2π(j-1)(r-1) /n ,j, r= 1, 2, …, n (5-58) 这类分子会出现简并轨道,且两个简且轨道是互为复数共轭,可把这两个轨道相加、相减而得到两个实的 简并轨道. 5.4.2 无机共轭分子 有些无机分子也具有离域 π 键,也可采用 HMO 方法处理.例如 NO2 分子,其中 N 原子轨道可形成 sp 2 杂化轨道,两个杂化轨道分别与两个 O 原子的 2pz 轨道形成两个 σ 键,另一个杂化轨道为 N 的孤对电子占 据.N 和 O 子的 2pz 轨道各有一个电子且 2pz 轨道相互平行,可形成离域 π 键.NO2 分子的结构示意图为 图 5.5.用 αN和 αO分别表示 N 和 O 原子 2pz 轨道的 Coulomb 积分,则其 HMO 久期方程为 อ 0 ߚ ∋െߙ ߚ ∋െߙ ߚ 0 ߙߚെ∈อ=0 (5-59) 由此方程容易解出三个离域 π 轨道的能量 ∈1= ଵ ଶ (αN+αO)+βටቀ ఈొିఈో ଶఉ ቁ ଶ 2 ∈2=αO ∈3= ଵ ଶ (αN+αO)-βටቀ ఈొିఈో ଶఉ ቁ ଶ 2 (5-60) N O O 2pz 2pz 2pz O N ∈1 ∈2 ∈3 图 5.5 NO2 分子成键示意图 图 5.6 NO2 的 π 轨道能级图 NO2 分子的 π 轨道能级图为图 5.6.NO2 含有三个 π 电子(2pz 电子),其中两个电子占据成键 π 轨道∈1,一个 π 电子占据非键 π 轨道∈2,形成了有三个中心(三个原子)和三个电子的离域 π 键,记为ߎଷ ଷ. 还有一些含有大 π 键的无机其轭分子.如 O3 是三角形构型,可形成三中 心四电子的大 π 键Πଷ ସ ;CO2 和NOଶ ା都是线型分子,如取键轴方向为 z 轴,则每 个分子的 2pz电子可形成一个三中心四电子的大 π 键ߎଷ ସ,2pz 电子也可形成一个 ଷߎ ସ,即每个分子有两个Πଷ ସ.类似的分子还有:N2O,Nଷ ି,BeCl2,HgCl2 等.碳 酸根离子 CO3 2-的结构为图 5.7 所示,能形成大 π 键ߎସ ,类似的分子还有NOଷ ି, SO3 和 BF3 等. 5.4.3 离域 π 键形成的条件 从以上这些例子可以看出,离域 π 键不仅仅限于单双键交错的共轭分子,凡是满足下列条件部可形成 离域 π 键: 图 5.7 COଷ ଶି的结构图 C O O O