
分子动力学简介
分子动力学简介
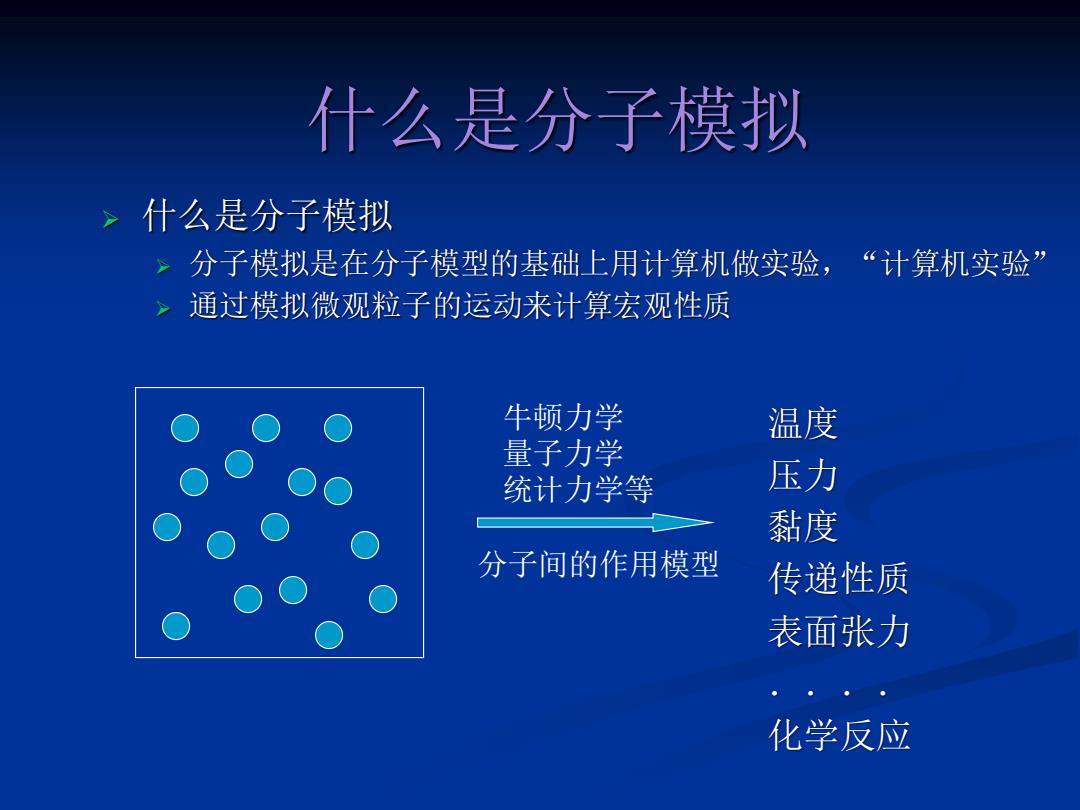
什么是分子模拟 什么是分子模拟 >分子模拟是在分子模型的基础上用计算机做实验,“计算机实验” >通过模拟微观粒子的运动来计算宏观性质 牛顿力学 温度 量子力学 统计力学等 压力 黏度 分子间的作用模型 传递性质 表面张力 化学反应
什么是分子模拟 ➢ 什么是分子模拟 ➢ 分子模拟是在分子模型的基础上用计算机做实验,“计算机实验” ➢ 通过模拟微观粒子的运动来计算宏观性质 温度 压力 黏度 传递性质 表面张力 .... 化学反应 分子间的作用模型 牛顿力学 量子力学 统计力学等
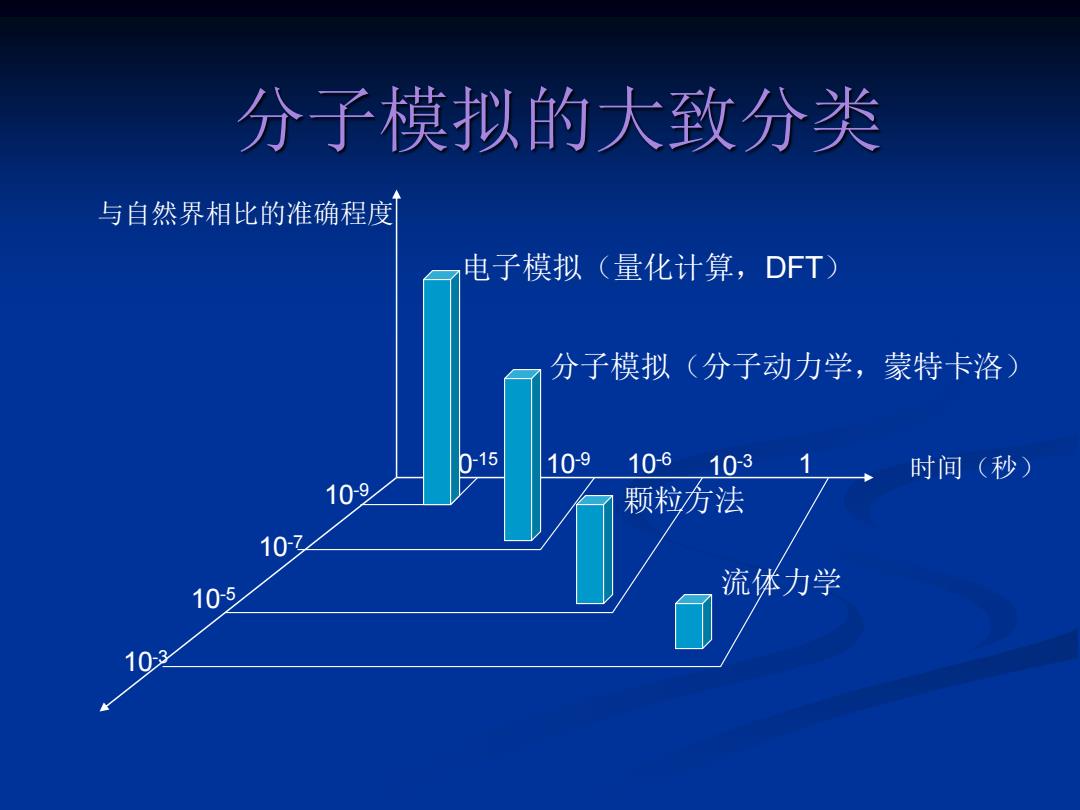
分子模拟的大致分类 与自然界相比的准确程度 电子模拟(量化计算,DFT) 分子模拟(分子动力学,蒙特卡洛) 0-15 109 10-6103 时间(秒) 109 颗粒方法 102 105 流体力学 103
分子模拟的大致分类 与自然界相比的准确程度 时间(秒) 10-9 10-7 10-5 10-3 10-15 10-9 10-6 10-3 1 电子模拟(量化计算,DFT) 分子模拟(分子动力学,蒙特卡洛) 颗粒方法 流体力学

量子力学模拟:ab nitio 原子结构 模拟电子 能量性质,化学键等信息 薛定谔方程 >量子化学计算 >一般处理几个到几十个原子 >常见软件:GAUSSIAN,NWCHEM等 密度泛函(DFT) >可以算到上百个原子 >常见软件:VASP
量子力学模拟:ab initio 原子结构 薛定谔方程 模拟电子云 能量性质,化学键等信息 ➢ 量子化学计算 ➢ 一般处理几个到几十个原子 ➢ 常见软件:GAUSSIAN,NWCHEM等 ➢ 密度泛函(DFT) ➢ 可以算到上百个原子 ➢ 常见软件:VASP

分子级别的模拟 分子水平的模拟 >以分子的运动为主要模拟对象 >采用经验性的分子间作用函数模拟微粒之间的作用 >一般情况下不考虑电子转移效应,因而不能准确模拟化学成键作用 >发展最早 >1950s,Alder.,劳伦斯利物默实验室,分子动力学模拟32个原子 >1950s,Metropolis,洛斯阿洛莫斯实验室,蒙特卡洛模拟32个原子 分子级别的模拟应用的领域很广 >广泛应用于化学,物理,生物,化工,材料,机械,治药等领域 >简单易学
分子级别的模拟 ➢ 分子水平的模拟 ➢ 以分子的运动为主要模拟对象 ➢ 采用经验性的分子间作用函数模拟微粒之间的作用 ➢ 一般情况下不考虑电子转移效应,因而不能准确模拟化学成键作用 ➢ 发展最早 ➢ 1950s,Alder,劳伦斯利物默实验室,分子动力学模拟32个原子 ➢ 1950s,Metropolis,洛斯阿洛莫斯实验室,蒙特卡洛模拟32个原子 ➢ 分子级别的模拟应用的领域很广 ➢ 广泛应用于化学,物理,生物,化工,材料,机械,治药等领域 ➢ 简单易学

蒙特卡洛方法 蒙特卡洛是一种优化方法 >通过蒙特卡洛算法来寻求能量最优点 >随机方法 >通过系综平均来求取宏观性质 模拟的是平衡状态,不涉及时间效应(KMC除外) 优点是可以跨越时间因素,缺点是得不到有关时间信息的 性质
蒙特卡洛方法 ➢ 蒙特卡洛是一种优化方法 ➢ 通过蒙特卡洛算法来寻求能量最优点 ➢ 随机方法 ➢ 通过系综平均来求取宏观性质 ➢ 模拟的是平衡状态,不涉及时间效应(KMC除外) ➢ 优点是可以跨越时间因素,缺点是得不到有关时间信息的 性质

分子动力学 分子体系 宏观性质 (几百~几亿)求解牛顿运动方程 F=- 6E Ot F=ma AX-Vul+a 可以模拟平衡状态,也可以模拟中间状态 ~可以获得有关时间的信息 >受时间的限制,无法模拟缓慢过程
分子动力学 ➢ 可以模拟平衡状态,也可以模拟中间状态 ➢ 可以获得有关时间的信息 ➢ 受时间的限制,无法模拟缓慢过程 分子体系 (几百~几亿)求解牛顿运动方程 宏观性质 2 0 2 1 V t at F ma E F = + = = −

CPMD:考虑量子效应的分子动力学 同时考虑原子核的运动(牛顿力学)和电子的运动(量 子力学) 能同时准确模拟物理作用和化学键作用 目前来说CPMD可以处理的体系还很小(几十个原子)
CPMD:考虑量子效应的分子动力学 ➢ 同时考虑原子核的运动(牛顿力学)和电子的运动(量 子力学) ➢ 能同时准确模拟物理作用和化学键作用 ➢ 目前来说CPMD可以处理的体系还很小(几十个原子)

颗粒方法(Coarse Grain) 将分子基团(几个或者几十上百个原子)当成单个的微 粒来处理 微粒之间的作用也是通过类似于分子动力学的未能函数 来描述 可以模拟更长的时间跨度 量子级别模拟 分子级别模拟 CG级别模拟 电子 原子核 原子
颗粒方法(Coarse Grain) ➢ 将分子基团(几个或者几十上百个原子)当成单个的微 粒来处理 ➢ 微粒之间的作用也是通过类似于分子动力学的未能函数 来描述 ➢ 可以模拟更长的时间跨度 电子 原子核 原子 量子级别模拟 分子级别模拟 CG级别模拟

势能模型 分子动力学的核心:牛顿运动方程 F=- OE Ot F=ma 势能(位能)模型:U(r)=fr) Ax-Wa >分子动力学对势能函数的依赖性:所有从分子动 力学计算出来得到的宏观性质最终都取决于势能 模型
势能模型 ➢ 分子动力学对势能函数的依赖性:所有从分子动 力学计算出来得到的宏观性质最终都取决于势能 模型 分子动力学的核心:牛顿运动方程 势能(位能)模型: U r f r ( ) ( ) = 2 0 2 1 V t at F ma E F = + = = −