
目 录 序言… e+tt0tt04t04▣0。单。。◆ 第一章薛定诨方程……1 1.1量子力学的历史背景……1 1,4 不含时间的薛定谔方程…11 1.2测不准原理…………4 1.5几率…………14 1.3含时间的薛定谔方程………6 1.6复数………16 第二章箱中的粒子………20 2.1微分方程………20 2.3一维自由粒子…28 2.2一维箱中的粒子…21 第三章算符… 0*……30 3.1算符………30 3.5三维箱中的粒子…43 3.2本征函数与本征值…33 3.6简并性……47 3.3算符与量子力学…35 3.7 平均值………………48 3.4三维多粒子的薛定谔 3.8合理波函数的要求…52 方程…………40 第四章谐振子…… …………57 4.1微分方程的幂级数解…574.2一维谐振子……60 第五章角动量…72 5.1几种物理性质的同时测 5.3 一粒子体系的角动量…81 定………72 5.4 角动量的阶梯算符法……97 5.2矢量………76 第六章氢原子… …………………105 6.1中心力问题……105 6.4 氢原子………116 6.2两粒子问题约化为一 6.5氢原子束缚态波函数……126 粒子问题……108 6.6类氢轨道…………135 6.3两粒子刚性转子……113 6.7塞曼效应………………141 第七章量子力学的定理…………147 7.1引言………147 7.4可对易算符的本征函 7.2厄米算符……148 数…………门 7.3按本征函数的展开……154 7.5字称……… 。2

7.6测量与态的叠加……169 7.8 量子力学公设……177 7.7位置的本征函数………174 √第八章变分法… 190 8.】变分原理…………………190 8.4 联立线性方程组………204 8.2变分法的推广………195 8.5线性变分函数………208 8.3行列式……197 第九章微扰理论 9.1引言…… …………216 9.6 八期方程的简化………243 9.2非简并微扰理论 …………217 9.7 氨第一激发态的微扰 9.3氦原子基态的微扰处理…224 处理………………246 9.4氨原子基态的变分处 9.8变分法与微扰法的比 理………………230 较…………255 9.5简并能级的微扰理论…235 9.9 微扰理论的技巧……256 √第十章电子自旋和泡利原理… *………………261 10.1电子自旋 ……261 10.6 锂原子……………275 10.2阶梯算符用于电子自 10.7 斯雷特行列式…281 旋…265 10.8锂基态的微扰处理…283 10.3自旋与氢原子…267 10.9锂基态的变分处理…285 10.4泡利原理…268 10.10自旋磁矩…………286 10.5氮原子………271 第十一章多电子原子… *290 ★11.1哈特利-福克自洽场 11.5多电子原子中的角 法……290 动量………308 11.2轨道与周期表………298 11.6 自旋-轨道相互作用…321 11.3电子相关…301 11.7 原子的哈密颜算符…325 11.4角动量的相加………303 第十二章分子的对称性… …4……331 12.1对称元素与对称操作…331 12.4对称性与光学活性…341 12.2对称操作的乘积…338 12.5对称点群…343 12.3对称性与偶极矩…340 第十三章双原子分子的电子结构……355 3

13.1玻恩-奥本海默近似…355 13.11电子几率密度……415 13.2原子单位…360 13.12偶极矩……418 13.3氢分子离子…361 13.13同核双原子分子的M0 13.4H安电子基态的近似处 和VB波函数……421 理……4…4…368 13.14H2的激发态…………425 13.5H激发态的分子轨道…382 13.15价电子近似……426 13.6同核双原子分子的分 13.16双原子分子的SCF 子轨道组态……389 波函数……427 13.7分子的电子谱项……395 13.17异核双原子分子的 13.8氢分子…402 M0处理…………436 13.9H2的价键法处理……406 13.18异核双原子分子的 13.10MO与VB理论的初 VB处理…………440 步比较…………411 第十四章维里定理和精尔曼-费恩曼定理……445 14.1维里定理………445 14.3赫尔曼-费恩曼定理……459 14.2维里定理与化学成键…454 14.4静电定理……463 第十五章 多原子分子的电子结构……472 15.1引言……472 15.8平面共轭分子的半经 15.2多原子分子电子谱项 验M0处理……522 的分类……472 15.9非平面分子的半经验 15.3多原子分子的SCF M0处理…559 M0处理………477 15.10 多原子分子的价健法 15.4水的SCFM0处理……482 处理……567 15.5定域M0……………491 15.11 化学反应………580 15,6甲烷,乙烷和乙矫的 15.12计算机与量子化学……587 SCF MO处理……501 15.13量子化学的未来………590 15.7分子的几何图形…517 附录…… 参考书目选… 习题答案选 …………612 索引… …………616 宁世光译

第一章 薛定谔方程 1.1量子力学的历史背景 十九世纪末,放电管和天然放射性的研究表明了原子和分子 是由带电荷的粒子组成的。电子带有负电荷。质子带有与电子电 荷大小相等符号相反的电荷,质子比电子重1836倍。原子的第三 种组分中子(1932年发现)是中性的,比质子略重。 1909年开始,卢瑟福(Rutherford),Geiger*和Marsden进 行了一系列实验,他们令一束α粒子通过一个薄的金属箔,让粒子 落在荧光屏上以观察它们的偏转。α粒子是从天然放射性蜕变得 到的带正电的氨核。卢瑟福观察到大多数“粒子基本上不偏转地 通过了箔,但是,出乎意外地,少数&粒子发生了很大的偏转,有的 反向折回。要得到大的偏转,电荷之间必须非常靠近,这样库仑斥 力才大。假如正电荷散布在整个原子中(如J.J.Thomson1904年 所建议的),一旦高能的:粒子穿过原子,按照经典静电学,斥力将 减小,并在原子中心变为零。于是卢瑟福断定,如此大的偏转只能 是在正电荷集中于一个很小而重的核时才能发生。 一个原子含有一个微小(半径10-18到10-12厘米)而重的核, 核由中子和Z个质子组成,Z是原子序数。核外有Z个电子。带电 粒子按库仑定律相互作用。(核子是靠强的短程核力结合在一起, 这对我们无关。)如气体动力学的结果所示,原子半径约1埃(1A ≡10-8厘米)。分子有多于-一个的核。 *译者注:本书中常见人名译成中文,并在首次出现时以括号写出原文;不常 见人名只写原文。 1

原子和分子的化学性质取决于它们的电子结构,所以提出电 子运动的本性和能量的问题。由于核比电子重得多,我们预期核 的运动与电子的运动相比较是微小的。 1911年卢瑟福提出了他的原子“行是”模型,其中电子在不 同的轨道上绕核运转,正如行星绕太阳一样。然而,这一模型有一 根本性的困难。按照经典电磁理论,一个加速的带电粒子以电磁 波(光)的形式辐射能量。一个电子以恒定速率绕核运转,由于其 速度矢量的方向连续变化而受到加速。于是卢瑟福模型中的电子 将不断地由于辐射而失去能量,因而将向核的方向盘旋。按照经典 (19世纪)物理学,卢瑟福型原子是不稳定的并且将要崩遗。 排除这个困难的-一个可能出路是1913年玻尔(Bohr)提出的 把能量量子化的概念用于氢原子。能量量子化由普朗克(Planck) 于1900年首次引入物理学,他以固体辐射的能量是v的整倍数 的假设开始,导出了观察到的热体(黑体辐射)发光的强度分布。在 hy中,y是辐射频率,h是一个比例常数(叫做普朗克常数),等于 6.6×10-27尔格·秒。1905年,爱因斯坦(Einstein)指出,光电效 应中释出的电子的动能与照到金属上的光的频率的依赖关系,可 由光是粒子样的实体(光子)所组成的观点来解释,每个光子的能 量 E先子=hv (1.1) 所以光除了表现为被衍射所证明的波动性外还能表现为粒子性。 玻尔假设氢原子中电子的能量是量子化的,电子只限制于在 一些允许的圆周之一上运动。当电子从一轨道(定态)跃迁到另一 轨道上,则吸收或放出一个频率为的光量子 v=△E/h (1.2) 式中△B是两个定态的能量差(能量守恒)。用一个假设,当一个 电子从自由(电离)态跃迁到某一束缚轨道时放出一个光子,其频 ·2·

率为在束缚轨道上电子旋转的经典频率之半的整数倍,玻尔用牛 顿力学推导了氢原子的能级公式。用(1.2),他得到了与观察到的 氢光谱一致的结果。但是,把玻尔理论适用于氦光谱的尝试是失 败了。而且,此理论不能用于说明分子中的化学键。 玻尔模型的根本困难在于用经典牛顿力学去说明原子中电子 的运动。显示不连续频率的原子光谱数据表明只有某些能量的运 动是允许的,即,电子的能量是“量子化”的。而牛顿力学允许能量 有连续变化范围。波动运动中的确出现量子化;例如,提琴弦的基 音和泛音频率。因此,德布罗意(de Broglie)于1923年提出电子 的运动可能有波的样子;即一个质量m和速率v的电子有一波长 入与之相联系,为 2=b三b (1.3) mo p 式中p是线动量。德布罗意用与光子类比的推理得出(1.3)式*。根 据爱因斯坦狭义相对论,任何粒子(包括光子)的能量可以表示为 E=mc2,其中c是光速。对于一个以速率c运动的光子,用(1.1) 得mc2=v=hc/,所以=h/mc=b/p。因而(1.3)式是电子的 相应的关系式。 1927年,Davison和Germer由观察从金属上反射的电子的 衍射效应,从实验上证实了德布罗意假说。1932年,Stern用氨原 子和氢分子观察到了同样的效应,这证明了波的效应不是电子独 有的,而是作为微观粒子运动的普遍规律的结果。(电子显微镜是 电子波动性的一个实际应用。) 电子在某些方面表现象粒子,在另些方面表现象波。我们面对 着物质(和光)的好似矛盾的“波-粒二象性”。怎能既是一个粒 子一一定域的实体,又是一个离域的被呢?回答是:电子既不是一 *译者注:原书中Eq.(X.X)一律译为(X.X)式
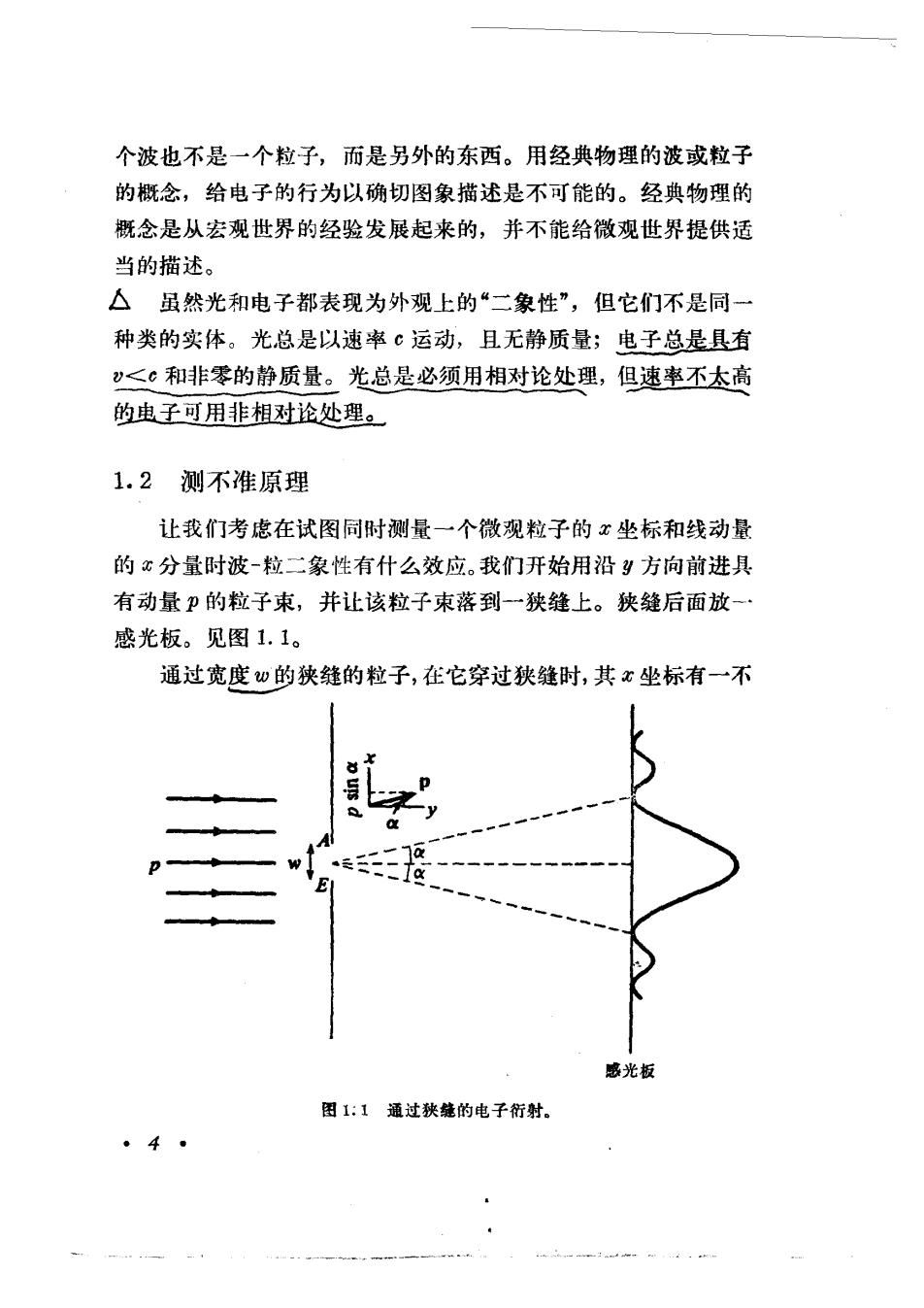
个波也不是一个粒子,而是另外的东西。用经典物理的波或粒子 的概念,给电子的行为以确切图象描述是不可能的。经典物理的 概念是从宏观世界的经验发展起来的,并不能给微观世界提供适 当的描述。 △虽然光和电子都表现为外观上的“二象性”,但它们不是同一 种类的实体。光总是以速率c运动,且无静质量;电子总是具有 <¢和非零的静质量。光总是必须用相对论处理,但速率不太高 的电子可用非相对论处理。 1.2 测不谁原理 让我们考虑在试图同时测量一个微观粒子的x坐标和线动量 的c分量时波-粒二象性有什么效应。我们开始用沿!方向前进具 有动量p的粒子束,并让该粒子束落到一狭缝上。狭缝后面放-· 感光板。见图1.1。 通过宽度w的狭缝的粒子,在它穿过狭缝时,其心坐标有一不 P 感光板 图1:1通过狭缝的电子衍射。 4

确定值0。称此x的展宽值为△,有△x=”。了二山) 由于微观“粒子”有波被动性,它们被狭缝衍射,在板上产生(象 光束那样)衍射图样。图1.1中,图线的高是到达指定点的粒子数 目的量度。衍射图样指出,当粒子被狭缝衍射时,它们的运动方向 改变了,从而一部分动量转移到x方向。动量的x分量是由动量 矢量在x方向的投影给出。一个向上偏转α角的粒子具有动量的 x分量为psina。一个向下偏转&角的粒子具有动量的x分量 一psina。由于多数粒子在一c到a范围内发生偏转,其中&是到 衍射图第一个最小处之角,因此我们取在中央行射峰展宽的动量 值之半作为动量的x分量的不确定值△Pz的量度:△pz=psinc。 于是 △xAPx=pwsina (1.4) 发生衍射第一最小的角度是容易计算的。第一最小的条件是: 在缝的上边缘通过缝的粒子与通过缝中央的粒子所经过的距离差 等于受,入是与粒子相联系的波的波长。从狭缝顶端发出的波和 从狭缝中心发出的波正好位相相反而彼此相消。从狭缝中点之下 距离d处发出的波与狭缝顶端之下距离d处发出的波相消。在图 1.2中作AC,使AD=CD,则路程长度之差为BC。狭缝到屏的距 图1.2第一最小衍射的计算

离比缝宽要大。因而AD与BD几乎平行。这使得角ACB基本上 是一直角,所以角BAC=&。于是路程差BC是wsin&。o令BC= 号1,得0sina=2,(1.4)式变为△Ap:=p。波长入由德布罗意 关系给出,1=h/p,于是△x△pz=h。由于不确定度尚未精确定义, 等号不真正确切,代之而写为 △x△p≈h (1.5) 这指出x和Px的不确定度的乘积是普朗克常数的数量级。在5.1 节中,我们将给出不确定度的精确的统计定义和精确的不等式以 代替(1.5)。 虽然我们只用了一个实验装置来说明(1.5),但它的正确性是 普遍的。不管做怎样的尝试,微观“粒子”的波-粒二象性对于我们 同时测定这样的粒子的位置和动量的能力是加有限制。位置测定 得愈精确,则动量测定得愈不精确。(在图1.1中,sina=/w,所 以狭缝变窄则增大衍射图样的宽展。)这个限制叫做测不准原理, 在1927年由海森堡(Heisenberg)发现。 由于波-粒二象性,测量动作在被测系统中引入一不可控制的 扰动。我们开始时用具有一精确P值(譬如为零)的粒子,由于加 一个狭缝,我们测量粒子的x坐标到准确度w,但此测量引入一不 确定度于粒子的Px值中,这个测量改变了体系的态。 1.3含时间的薛定谔方程 经典力学只适用于宏观粒子。对于微观“粒子”,需要一个新 形式的力学,叫做量子力学(或波动力学)。现在考虑经典力学与 量子力学之间的一些对比。为简单起见,我们处理一维的一粒子 体系。 经典力学中粒子的运动服从牛顿第二定律: 6●

d2x F=m dt? (1.6) 式中F是作用于粒子的力,m是粒子的质量,t是时间。(1.6)式 含有坐标x对t的二阶导数。要解它必须进行两次积分。这样在 解中引入二个任意常数c1和c2,于是 =g(t,c1,C2) (1.7) 9是飞的某个函数。现在问,在给定时刻t。必须具有什么情况才 能预知粒子的未来运动?如果知道在t0时粒子在x0点,则有 x0=9(t0,C1,c2) (1.8) 由于有两个常数要确定,还需要知道更多的情况。微分(1.7),可 得 =0=品9,c,) dx 式中)是粒子的速度。如果也知道在t。时粒子具有速度0,于 是有另外一个关系式 d gi9(t,c1,c2) (1.9) 则我们可用(1.8)和(1.9)去解c1和c2,以和t0表示。知道了 c1和c2,可用(1.7)式去预期粒子确切的未来运动。 “态”字在经典力学中意味着体系的每个粒子在某一瞬间有确 定的位置和速度,以及有确定的力作用于粒子上。按牛顿第二定 律,给出在任何时刻体系的态,它的未来的态和未来的运动是完 全确定的。牛顿力学在解释天体运动时的深刻成功,使得许多哲 学家用牛顿定律作为哲学决定论的论据。数学家与天文学家 Laplace(1749一1827)认为字宙只不过是由服从牛顿定律的粒子 所组成。所以,给定某时刻字宙的状态,字宙中一切事物的未来运 动是完全决定了的。若有超然能力知道在任一时刻字宙的状态, 就可在原则上计算所有的未来运动