
目录 第一章系综理论… …………………(1) 1基本假设… (1) $2正则系综· (3) 3巨正则系综 (18) 4自由粒子系统 (25) 5经典统计 (57) 6非理想气体 (72) 第二章趋向平衡的过程 ………(83) 7维(Liouville)定和彭加(Poin- caré)周期 ……………… …………(83) 8H定理 (88) $9 Ehrenfest模… (91) 第三章凝聚理论与合作现象 (105) 10体积有限系统的性质 (105) 11容积为无限时的极限 (109) 12相变…… (119) $13有序-无序转变、伊辛模型和格气………… …(124) 14平均场近似………… (133) 15临界指数的标度假设… (142) 16矩阵方法 (144) 第四章量子统计法 (182) $17量子统计中的维里展开式 (182) 18超流现象 (193) 附录证明梅耶第二定理 (196) 习题… (207)

第一章 系综理论 统计力学的研究目的,是对各种宏观系统的所有与时问无关 的性质进行统计分析.我们主要讨论宏观系统平衡现象的理论, 而非平衡态现象不是我们主要的研究对象.目前对非平衡态所取 得的进展是发现过去的趋向平衡的理论不正确,纠正了一些错 误,但问题并没有很好地得到解决」 平衡态系综理论是研究宏观系统已经达到平衡之后的各种热 力学性质。 我认为统计力学是理论物理中最完美的科目之一,因为它的 基本假设是简单的,但它的应用却十分广泛 物理学的研究目的是探求自然界的基本原理,这种基本原理 是简单的,其数学表达形式也不一定复杂,但其应用的领域一定 很广泛.统计力学就具备这一特点.现在我们就从统计力学的基 本假设开始 §1基本假设 设有一定体积的宏观系统,其哈密顿量是登,它的本征态 (本征矢量)为的,本征值为8(即能量),标准的壁子力学本征值 方程为: 中=6的. (1.1) 假如,考虑由W个相同粒子组成的宏观系统,每个粒子的质 量为m,而第:个粒子的动量用卫:表示。如动能用非相对论性的表 达式,势能仅考虑粒子间的对相互作用,即势能仅与r有关, 则哈密颜量就是 =p」 (1.2)

在公式(1.2)中,求和号)表示对所有的粒子对数相加.其 t>i 中N是一个非常大的数目,它表示宏观系统. 第j粒子· 假设我们只知道系统的总能量在E和E一 △E之间,动量在卫和p+△p之间,除此之外, 我们并不知道到底系统处在哪个本征态上,设 用2表示所有符合特定条件下的本征态的总 数.显然?应是E,△E,p和Ap的函数,即 第粒 2=2(E,△E,p,△p,…). (1.3) 现在:我们要问:发现该系统处在这2个可 能本征态中某特定术征态的几爷是多少? 答案是很简单的,果我们不知道它在:娜个状态1上,我 以假设它在:每个态上的儿*是相等的,即 1 p(几举)· (1.4) 公式(1.4)就是流计力学平衡态的唯…基本假设 我们以后将詹到,就是这个毕本假设,师上不同的哈密顿量 就可使我们研究各种复杂系统的祖变现象,从固态到液态或从 液态到气态的转化,以及超导等等. 应该指出:,以上这个假设是任何统计问题所通用的.因此, 它也是一个相当普遍、自然的假设. 例如,掷骰子、打桥牌等游戏.骰了有六个面,我们问某-一 特定面向:的几率是什么?或问打桥牌时,人们随衬地取出任何 一张特定的牌的几率是什么?很自然地回答,它们的儿率分别为 合和品 那么到底掷骰子出现某一特定面的儿率是否就是。呢?这要 取决于是不有人在骰子内捣鬼,如果有人将骰子内充以水银,那结 2

果就不会是】.如果经过实际的投滨发现现的儿率与计算的结 6 果不符,那一定有某些周定的条件未计入·经过研究弄清这些条 件后,再把它圳进去,果就相符合了. 到此为止,我们并未要求粒子的数日N>1,只求状态数 牛0.以后我们将说明为计么要用到粒子数要足够多这个条件 S21 正则系综 设H表示V个料问粒构成的非相对论性系纺的哈密顿 量 (2.1) 它的本征值方程是 H中y=E1. (2.2) 其中中是系统的第个术征态,E,是相应的木征值.其实,N不 一定是固定的,如对光子米说,其数日是不固定的,哈密顿量也 不是非相对论的,在始阶段可先来时论固定粒子数和非相对论 性的情形.然后到推广到相对论情形 我们的目标是求出系统的热力学函数,如亥姆霍兹白山能、 吉布斯热力势、熵等等. 这个问题的求解方法是:先想像山M个相同的系统组成一系 综,每个系统均由N个相同的粒了组成,其哈密顿量为H,H2, H,…,系统与系统问的热接触用线表示,表示可以交换热量. 由于各个系统是处在不同位置,封此是可以区分的.如1.1所 示. 系综的总哈密顿量为,它应该等于各个系统的哈密顿址之 和再加上线的热交换对哈密顿量的贡献.我们用“热交换项”表 示这部分的贡献,每个系统的哈密顿量H。都是相同的,所以总 3

的哈密顿量是: 一四闪可 系统标号a“】 图1.1 (系综)-∑H。+“热交换项”. 系综的哈密顿量写成以上形式是所有进行统计问题者所具备 的 通常掷骰子游戏是把时间延长,进行无数多次投掷求得其几 率的.但是也可以把无数多同样的骰子分散给众人,让众人在相 同条件下同时掷骰子(系综)来实现.这两种办法是一致的,因 此,以上把许多同样的系统放在一起构成系综是进行统计的一个 基本的方法」 正则系综是我们用来研究通常热力学系统与外界有热交换, 但源度一定的情况.如图1.1中有热接触线的系统,只要每个系 统足够大,在物理上就可使得热交换足够的小,以致于认为是完 金可以被忽略的.但是,如果系统中只有几个粒了,就不可能有 比系统本身小得可以被忽略的热交换项了.所以说只要是一个宏 观系统,其热交换项就是完全可被忽略的.在这种条件下,系综 的总哈密顿量就可写成各个系统的哈密顿量之和,系综的本征态 就是各个系统本征态之积: 2(系综)=∑H, (2.3) (系综)= (2.4) 凡是符合以上条件的系综就是正则系综.正则系综是用来研 究固定温度的系统的.要使系统的温度不变,就要和一个大热库 相接触。在系综中这个热库就相当于除该系统外的其他全部系统 4

之和. 正则系综给定后,假设只知道系综总能量为8,但并不]道 某系统处在哪个态,我们要问,某系统处在中;态上的儿率是 多少? 设M裘示在中态上的系统数,E,表示第j个态的能量.显 然,总的系统数 M=2M, (2.5) 系综的总能量 8=M,E,. (2.6) 尽管我们知道了总能耻和总的系统数M,并且给定了一分 布{M},但是各系统的状态仍然没有完全确定.例如,已知有3 个系统在j:态,5个系统在j2态,但是到底哪3个系统在j态,哪 5个系统在2态,还是不确定的.很容易证明,对某一给定分布 {M},系综的态数2为 IM小 (2.7) 证明如下: M个系统所有不同排列的总数是M!,但是在同一状态的系统 之间的交换并不产生新的态,因此,应该把它们除去,于是(2.7) 式得证 现列举一简单的由三个系统构成的小系综为例加以说明,即 M=3. ()如一个系统在j,态,两个系统在j:态,所以系综的态 31 数0-1121 3. (i)如有三个系统在j:态,有0个系统在i:态,所以系综 31_ 的态数2=0131 =1 5

这些简例的果是明显可见的.同理,当M很大时也是正确 的。 由此可知,尽管给定了8,M和分布{M;},系统的状态并不 确定.另一方间,如采仅仅给定了后和M,{M,》分布并不确定, 我们要问,哪种分布《M}的儿率最大?根据(1.4)式的基本假 设,每种分布几率应与所对应的态数2成正比,因为态越多,几 率越大,对分布几率求极大值,就是求2的极大值.利用求微商 的方法并光虑到(2,5)和(2.6)式对M利8给定的约束条件,要引 入两个拉格朗日乘子α和B.所以极值的条件是 a a(∑M)3Me,) aMij Ing-a -=0.(2.8) aMi OM 要淮确计算几落就要要求系综中的系统数很大,但系统本 身不一定很大,任何统计分析问题必须要重复非常多次同样的过 程才能得到较正确的几率.以掷骰子为例,掷骰子的次数越多, 几率就越接近某-一固定数,这见做-·切统计问题的方法,它并不 是一个假设.当M趋向无穷大时,相应地,各M;也趋向无穷大 对于M》1,可以用斯特灵公式(Stirling formula)来近似地代替 阶乘: M1-(0'2a1++a88M+… (2.9) 这一公式收敛得很快,郑使M不很大也是一个很好的近似公式」 读者可以自行证明这一公式.利用斯特灵公式得到 lnQ=MnM-M-∑M,lnM;+∑M. (2.10) 在对?求偏微商时,有两种不同的方法.一种方法是视I 为固定.另一种方法是视M为M:的函数,因此也要对M求偏微 商.不过,所得的结架是一致的,只是α的值相差一个常数.为 简便计,我们采用M面定的方法,得出 6

OIn OM; =一lnM, (2.11) aM 2Mi =1, (2.12) 88=E: a (2.13) 将以上(2.11)、(2.12)和(2.13)式代入(2.8)式得 --In M;-a-BE=0, (2.14) 即 In Mj=-a-BEi, (2.15) 所以 Mj=e-a-BEi. (2.16) (2.16)式表示在正则系综中,在系统数M给定和总能量8周 定的条件下,系统处在第j态上的儿率最大的分布.式中出现了 两个常数a和B,以后对B的物理意义还要讨论, 定义P,表示最大几率分布时,系统处在第j态的几率: e-BE Pi=M (2,17) 2 e-BEj 定义 配分函数Q=∑eE1. (2.18) 它表示各个状态的相对儿率之和.在(2.17)式,配分函数是 作为归一化因子出现的 在求P时就消去了α因子,B因子可以出系统的平均能量 E=哥 (2.19) 来确定, E=古Be. (2.20) 这个等式给出一重要结果:在正则系综中,给定至,而M趋向无 7

限大时,P;和B与M无关. 下面再来证明,在给定系统的和E,当M趋向无穷大时, 以上的几率最大分布就是真实的分布,换言之,涨落趋向于袋 证明如下: 试考虑一函数 f=f(M)=ln2-a∑M-B∑ME1,(2.21) 手达到极值的条件为 af OM; =0. (2.22) 达到极值时,M,=MP;三亚;,P;与M无关. 而 a'f 8'InQ 1 aMaM “i,<0. (2.23)》 由于f的第二项和第三项均为M;的一次式,故对M:二阶以上的 微商均为零。只剩下第一项取不为零的负值.这表明极值是稳定 的. f对M;每求一次微商,其分母就增加一个M:因子.由于 →c∞,M→c∞,所以高次微商很快地趋向零. 用泰勒级数把f(M)在及附近展开: )-)+子 af (M;-)+ +2号影M,-r+ (2.24) =-f(及)-22MP(M1-,)× x{1+o(x)以 (2.25) 8
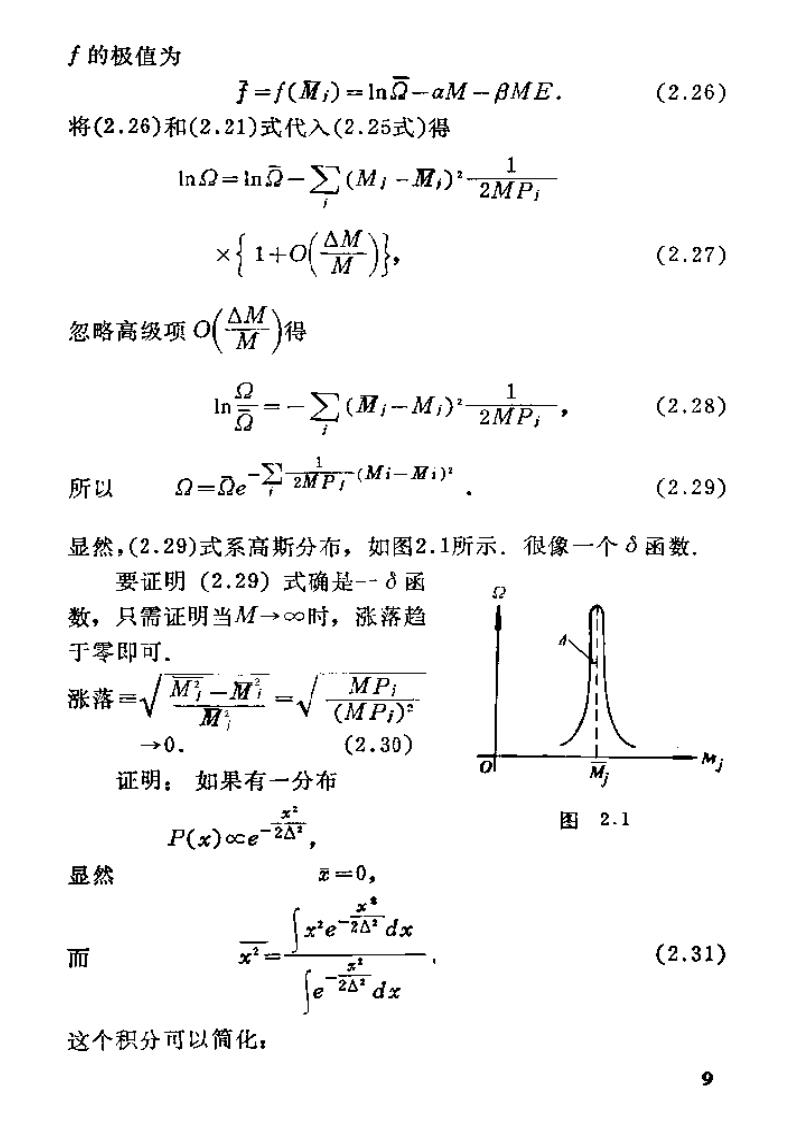
手的极值为 子=f()=ln-aM-BME. (2.26) 将(2.26)和(2.21)式代入(2.25式)得 ln2=n2-∑(M1-,)22MP, ×{1+o(以, (2.27) 忽略高级项0(器)舟 ∑(及1-M)22MP,, (2,28) 所以 Q=DeP (Mi-i) (2.29) 显然,(2.29)式系高斯分布,如图2.1所示.很像一个8函数. 要证明(2.29)式确是--6函 2 数,只需证明当M→∞时,涨落趋 于零即可. 涨落三√ 福--√ MPi (MP)? →0. (2.30) 0 M 证明:如果有一分布 M P(x)ce-2」 图2.1 显然 2=0, xt x'e 26dx 而 x- (2.31) e 2A dx 这个积分可以筒化: 9