
A 目 录 第一编 统计力学基础 (环少讲 第一章相空间及Hamilton方程 S1.1体系状态的描述… (3) (一)坐标-坐标空间 (二)坐标-速度空间 (三)坐标-动量空间 1.2运动方程… ·(32) 第二章统计系综和Liouville定理 (22) S2.上统计系综和相密度… …(23) S2.2Li0 aville定理… (27) §2.3统计平衡和Gibbs分布… (34) (一)统计平衡和微正则系棕 (二)正则系粽和 配分函数(Partition function) (三)巨正 则系综(Grand Canonica1 Ensemble) 习题… (47) 第三章经典分布定律 (49) $3.1近独立子系的最可几分布…… (49) S3.2 Maxwell1速度分布律… (65) S3.3能量均分原理… ……(68) (一)统计力学中的苹均值 (二)能量均分原理

甘录 §3.4理想气体状态方程式…(73) 习题…… (74) 第四章量子统计及其应用 (75) §4.1由经典统计向量子统计过渡 (75) (一)微观运动状态的描速 (二) 统计系棕 (三)统计假设 (四)几率计算 §4.2量子态和量子态数… (79) S.3粒子全同性和量子统计法… (96) (一)徽观粒子的不可区别 (二)Bosa- instim统计(1924年) (三)Fermi--Dirac 统计(1926年) (四)三种统计的比较 S4.4Bose-Einstein统计和Fermi--Dirac统计 的应用……… (110) (一),光子气的统计性质 (二)电子气的统计性质 §4.5固体热容理论… (116) (一)固体热容的经典理论 (二)Einstein理论 (1907年) (三)Debye理论(1912年) 习 暫… (124) 第二编 独立系统计热力学 第五章 嫡 (129) §5,1熵S与最可几率形mx… (129) $5,2熵S与微观状态总数2… (133) 85.3摘S与信息… (138) (一)信息论概2 (二)信息论的热力学意义 习题+ (145) 第六章热力学与统计力堂 (147)

第二编 独立系统计热力学 3 6.1从熵的统计力学定义出发导出热力学量 O4.044.14.... (147) (一)Gbhs自由熊G (二)Helmholtz自由 能F (三)熵S(四)内能U (五)热焰 H (六)热容C,和C 6.2从Maxwell-Boltzman.n分布出发导出热 力学量… (150) ()内能U (二)功8形 (三)热8g (四)熵dS (五)其它各热力学函数 (六)培H §6.3热力学量围绕平均值的涨落… (157) (一)正则系综、徽正则系棕中能量、压强的涨落 (二)巨正则系综中压强、密度的涨落 (三)系 综的热力学等价性 习题… (162) 第七章 配分函数的性质与计算 (164) §7,1配分函数的一般性质… (165) (一)配分函数按能量的分高 (二) 零能级效应 7,2平动配分函数…… (168) (一)平动配分函教Q: (二) 平动热力学函数 7.3转动配分函数… (174) (一)直线型喇性分子 (二)线型刚性分子 §7.4原子,单原子分子配分函数… (13) (一)电子配分函数Q。 (二)核自旋配分函数Q。 S7.5·双原子分子配分函数…… (196) (一)Q,与核自旋效应 (二)H分子的ortho- H亡Para-Hz平衡和钱动热容 (三)双原 子分子的振动配分函数Q

目 录 $7.6多原子分子配分函数… (208) ()简正坐标和简正振动 (二) 多原子分子振 动配分函数 习 题…… (216) 第八章 配分函数的应用 (218) 8.1平衡常数的计算… (218) (一)化学平衡的条件 (二)化学位的统计力学 表达式 (三)平衡常数的统计力学表达式 (四)核自 旋效应与等分子交换反应 (五)平衡常数计算示例 §8.2绝对熵值的计算……(240) (一)热力学第三定律和嫡的绝对值 (二)残余熵 8.3表面吸附的统计理论…… (252) (一)引言 (二)理想可动单分子层吸附 (三)理想定城单分子层吸附 (四)理想定城多 分子层吸附 习题 (262) 第三编 相关系统计热力学 第九章 分子间力和分子势能函数 (267) §9.1 分了间力的来源和类型………… (267) S9.2 定向作用(Keesom力) (269) 9.3诱导作用(Debye力) (273) §9.4色散作用(London力) (276) $9.5分子势能函数… (282) (一)分了间排序能 (二)分了势能函数 第十章 真实气体 (287)

第编相关系统计热力学 §10.王真实气体状态的经验方程… (287) S10.2 相关系配分函数与构型积分…… (290) $10.3真实气体状态方程与热力学量… (299) (一)状态方程式 (二)逸度 S10.4刚球势函数和Van der Waals气体… (303) (一)刚球模型 (二)Van der Waals气体 S10,5真实气体与双倒幂势函数………… (307) 习题 (311) 第十一章液体和溶液的统计理论… (313) S11.1液体的“格子”理论… (314) (一)“自由容积”模型 (二)谐摄子模型 (三)Lennard--Jones(12-6)势函数模型 §11.2液体理论的分布函数法…… (326) (一)分布函数与相关函数 (二)液体的热力学 量 (三)径向分布函数的确定 §11.3溶液的似晶格模型理论… (337) (一)理想溶液 (二)正规溶液 (三)无热 溶液 (四)一般溶液 (五)高分子溶液 S11.4电解质溶液理论…… (356) (一)Debye-Hakel理论 (二)Pitzer理论 习题……… (381) 第十二童速率过程的统计理论 (383) §12.1分子碰撞… (383) (一)气相中分子碰擅 (二)溶液中分子碰撞 $12.2气相中的输运过程… (4033 (一)粘度系数 (仁)热传导 (三)扩散 系数

6 目 录 S12.3化学反应的分子碰撞理论… (413) (一)反应速度常数的计算 (二) 几何因了P 的计算 §12.4活化络合物理论 (417) (一)反应速度常数的一般表达式 (二)过渡态 的热力学 §12,5单分子反应理论… (429) ()RRK方程 (二)RRKM方法 $12.6液相和溶液中的输运过程… (436) (一)液体的粘度 (二)溶液中的扩散 附 录… (449) ,A.数学附录 (449) B.求统计平均值的Darwin-Foler方法… (469) C,物理常数 (474) D。能量换算因子 (475) 参考文献… (476)

第一编 统计力学基础

第一章 相空间及Tamilton方程 §1,1体系状态的描述 统计力学从其开创就采纳了原子-分子论。它把原子、分 子等看作力学体系,根据经典力学定律,可以指定分子在某方 向上的速度或动最及其空间位置。如果作用力的性质与一个质 点在某时刻的位置和速度已知,那么,以后任何时刻的位置和 速度都能预言。但是,计算一个多质点体系的运动是极端困雅 的。在统计力学中,-·般研究的体系都含有约103个粒子, 这些粒子运动的精确讣算非常复杂,因此实际上不可能做到。 统计力学的任务是从微观力学性质出发得到宏观热力学性质, 统计力学这一目的只有运用统计方法才能实现、事实上,体系 粒子数越多,统计方法得到的结论就越可靠。 粒子运动的位移(坐标)与速度、动量随时间变化,则粒 了在某瞬时的运动状态将由相应的坐标、速度或动量等数值来 确定。下面介绍描述粒子运动状态的方法: (一)坐标-坐标空间 一个粒子在空间中的位置,可以 用坐标-坠标空询中的一点来描述。选择什么坐标系,要根据 所研究的问题性质来确定。 例如,一个粒子在平面上运动时,可以刑笛卡尔坐标系来
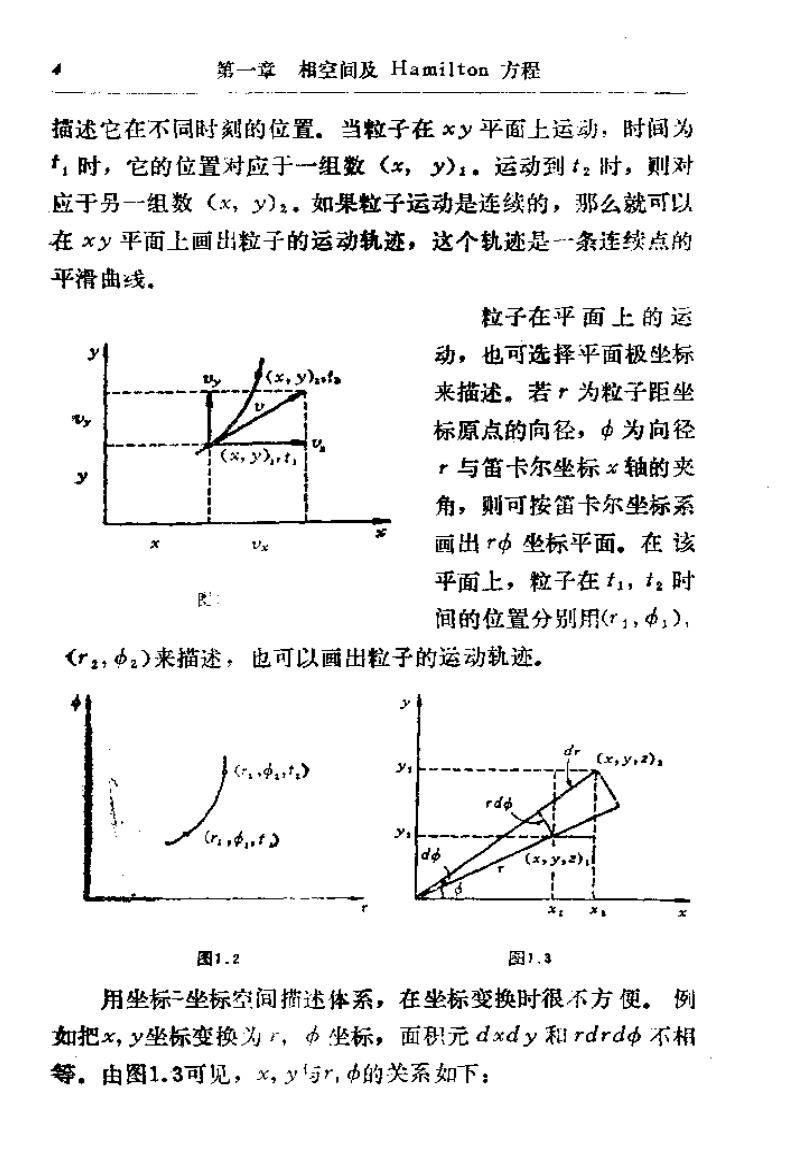
第一章相空间及Hamilto如方程 描述它在不同时刻的位置。当粒子在xy平面上运动,时间为 t:时,它的位置对应于一组数《x,y):。运动到t2时,刘对 应于另-一组数(x,y),,如果粒子运动是连续的,那么就可以 在xy平面上画出粒子的运动轨迹,这个轨迹是~条连续点的 平滑曲线。 粒子在平面上的运 动,也可选择平面极坐标 (¥,y)a 来描述。若”为粒子距坐 标原点的向径,中为向径 (,yt ”与笛卡尔坐标×轴的夹 角,则可按笛卡尔坐标系 V 画出r中坐标平面。在该 平面上,粒子在t,t2时 间的位置分别用(x1,中,), (”z,中2)来描述,也可以画出粒子的运动轨迹。 C,y,2), (r,1,t (x,y) 图1.2 图1.3 用坐标二坐标空间描述体系,在坐标变换时很不方便。例 如把x,y坐标变换为,功坐标,面元dxdy和rdrd中不相 等。由图1.3可见,x,y与r,b的关系如下:

11体系状态的描述 5 x=rcosd 1.1) y =rsind (1.2) 根据多直积分变量变换原理,则有 dxdy=Jdrdd (1.3) 式中J是变换因子,称Jacobi行列式。 Jm(%,y) a(r,中) ax ax ar coso -rsind ay ay sind rcosd ar 3中 =rcos2中-(~rsin2)=r (1.4) dxdy=rdrdd (1.3) 可见,用坐标-坐标空间可以描述粒子,在运动中各时间 的位置,但是在统计力学坐标变换的数学处理中是不方便的。 描述粒子的运动状态除要确定它的位置外,还要确定其运 动速度。速度是-一个矢量。粒子在其运动轨迹上任何一点的速 度方向,总是在该点的运动轨道切线方向上(图1.1)。速度 在坐标轴x和y上的投影为v.和v。因此速度的大小为: v{=√w+u 粒子在运动中,速度的大小和方向都可变化。可以用速度速度 空间来描述粒子的运动。例如可用二维平面速度空间(v,,) 中的一点来描述在平面上运动的粒子的速度。 显然,可以用固定质点在一个三维坐标空间中的位置和在 另一个三雄速度空间的速度来街述质点的运动状态。但用两种 坐标空间很不方便。 (二)坐标-速度空间 我们可以设计一种坐标-速度空