复旦大学：《统计热力学》课程教学资源（课件讲稿）04 Chapter 4 经典统计和量子统计

已包H厄5 Chapter 4 经典统计知量子统计 经典力学中的系综 经典Boltzmann绕计 从量子统计的经典过渡 从量子统计到经典统计

Chapter 4 经典统计和量子统计 经典力学中的系综 经典Boltzmann统计 从量子统计的经典过渡 从量子统计到经典统计

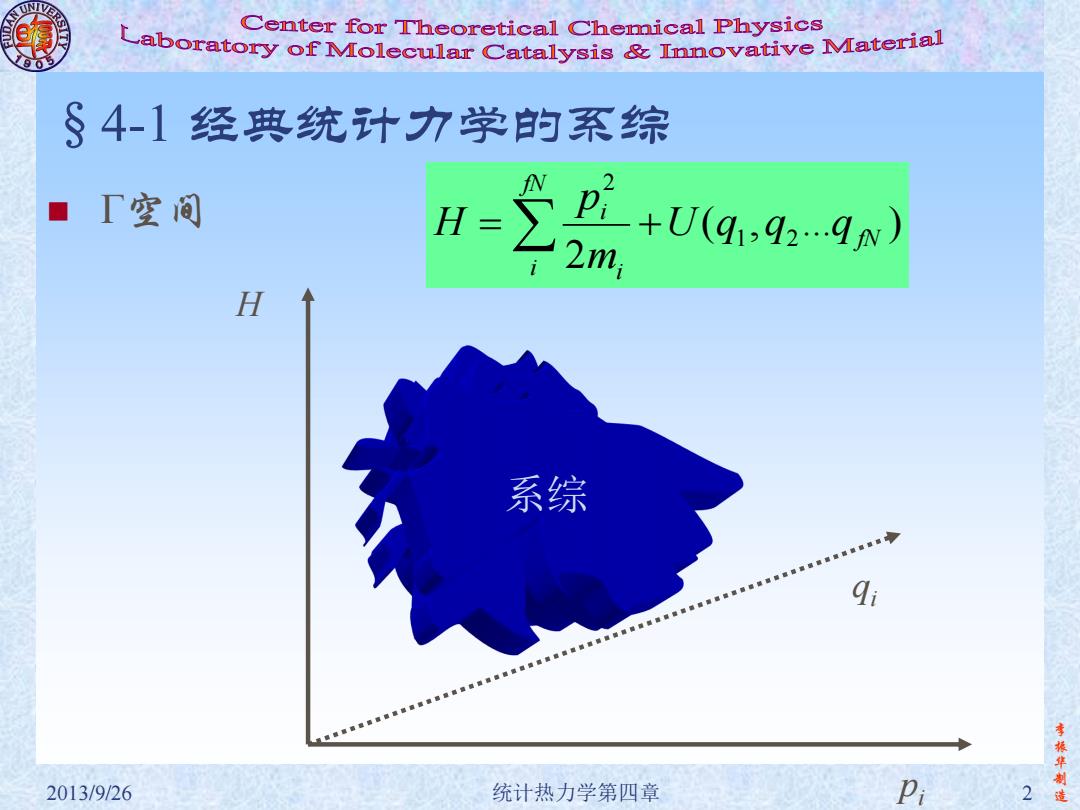
UN Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material §4-1经典统计力学的系综 ■「空间 H-a49 2m H 系综 李振华 2013/9/26 统计热力学第四章 2 造

李 振 华 制 2013/9/26 统计热力学第四章 2 造 §4-1 经典统计力学的系综  Γ空间 H qi pi ( , ... ) 2 1 2 2 fN fN i i i U q q q m p H    系综

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 系综的一些性质 系徐密度 由于系综中含有体系的数目是非常巨大的，所以体系从 像空间的一个区域到另一个区域的变化实质上可看作是 连续的。因此在「空间中相，点密度可作为连续函数处理。 △N dN p(p,q,t)=lim △T→0 pD,9,)的物理意义是在点g1,92…,9,和p1P2…Pn处的无 限小体积元dT内的相点数。 dr=dq dqzdq dp dpzdp 显然， N=∫dW=∫pr=jjp(p,d,t)dgp 李 华制 2013/9/26 统计热力学第四章

李 振 华 制 2013/9/26 统计热力学第四章 3 造 系综的一些性质  系综密度  由于系综中含有体系的数目是非常巨大的，所以体系从 像空间的一个区域到另一个区域的变化实质上可看作是 连续的。因此在Г空间中相点密度可作为连续函数处理。 dΓ dN Γ N p q t Γ      0 ( , , ) lim ρ(p, q, t)的物理意义是在点q1 ,q2 ,…,qfN,和p1 ,p2 ,…,pfN处的无 限小体积元dΓ内的相点数。 1 2 1 2 ... ... fN fN dΓ  dq dq dq dp dp dp 显然，    N  dN  d  ( p, d,t)dqdp

Center for Theoretical Chemical Physics aboratory of Molecular Catalysis Innovative Materia 系综的一些性质 ■ 几率密度 在T空间中，dN个相点在某一体积元dT出现的几率为： dN p(p.q.t)dP(p.q.t)dr N N 定义函数，9，)： f(9,p,)=Pp,9 称为相点的几 率密度或系综分布函数，容易证明，它己经是归一化函 数： N=p(p.q,t)dI 1-Da-(p.. 振华制 2013/9/26 统计热力学第四章

李 振 华 制 2013/9/26 统计热力学第四章 4 造 系综的一些性质  几率密度  在Γ空间中，dN个相点在某一体积元dΓ出现的几率为： dΓ N p q t N p q t dΓ N dN ( , , ) ( , , )   定义函数f(p, q, t)： 称为相点的几 率密度或系综分布函数，容易证明，它已经是归一化函 数： ( , , ) ( , , ) 1 ( , , ) N p q t d p q t d f p q t d N            N p q t f q p t ( , , ) ( , , )  

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 系综的一些性质 Liouville(刻推)定理 保守力学体系在相空间里相密度在运动中不变 化，或者说相密度守恒，即： dp(p,9,0=0 df(p,q,t) dt dt 证明思路：由于每一个相点肯定是随时间运动，即下 一时刻从相空间的这个位置（小体积元）移动到下一 个位置（另一个小体积元)，所以让我们来看这些相 点移动的情况。 振华制 2013/9/26 统计热力学第四章

李 振 华 制 2013/9/26 统计热力学第四章 5 造 系综的一些性质  Liouville（刘维）定理  保守力学体系在相空间里相密度在运动中不变 化，或者说相密度守恒，即： 证明思路：由于每一个相点肯定是随时间运动，即下 一时刻从相空间的这个位置（小体积元）移动到下一 个位置（另一个小体积元），所以让我们来看这些相 点移动的情况。 0 ( , , )  dt d p q t 0 ( , , )  dt df p q t

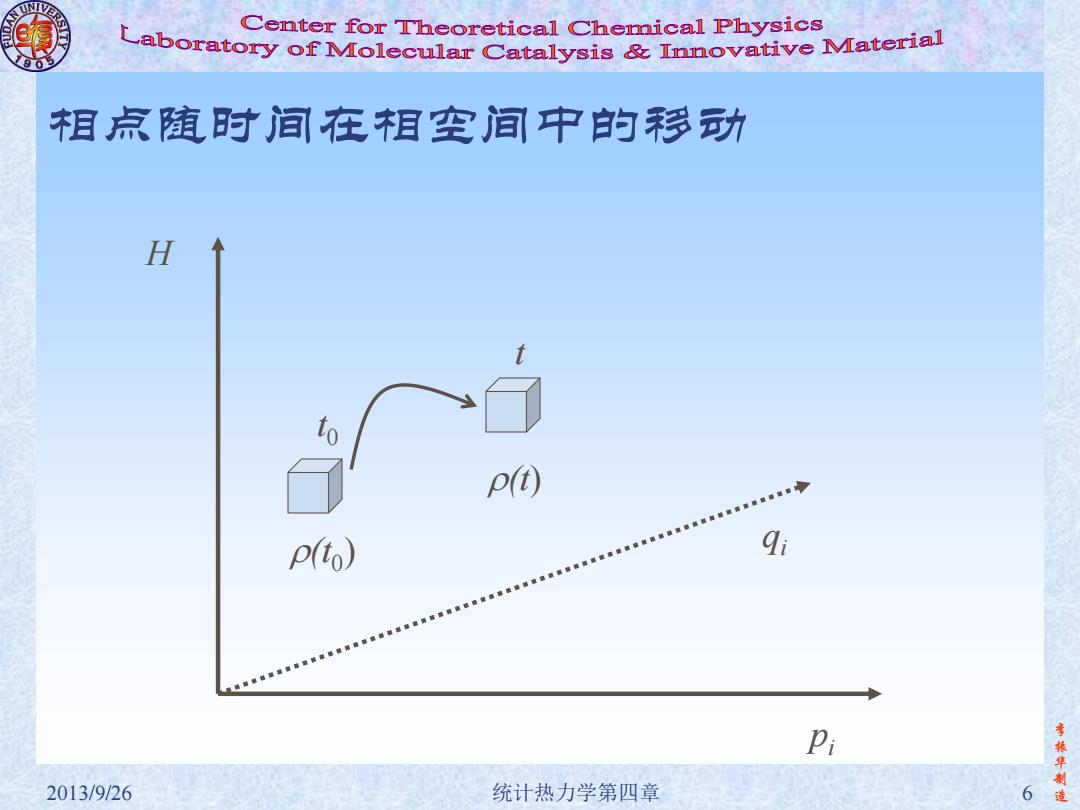
UN Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 90 祖点随时间在祖空间中的移功 H p(t) p(t) Pi 李振华 2013/9/26 统计热力学第四章 6 造

李 振 华 制 2013/9/26 统计热力学第四章 6 造 相点随时间在相空间中的移动 H qi pi t0 t (t0 ) (t)

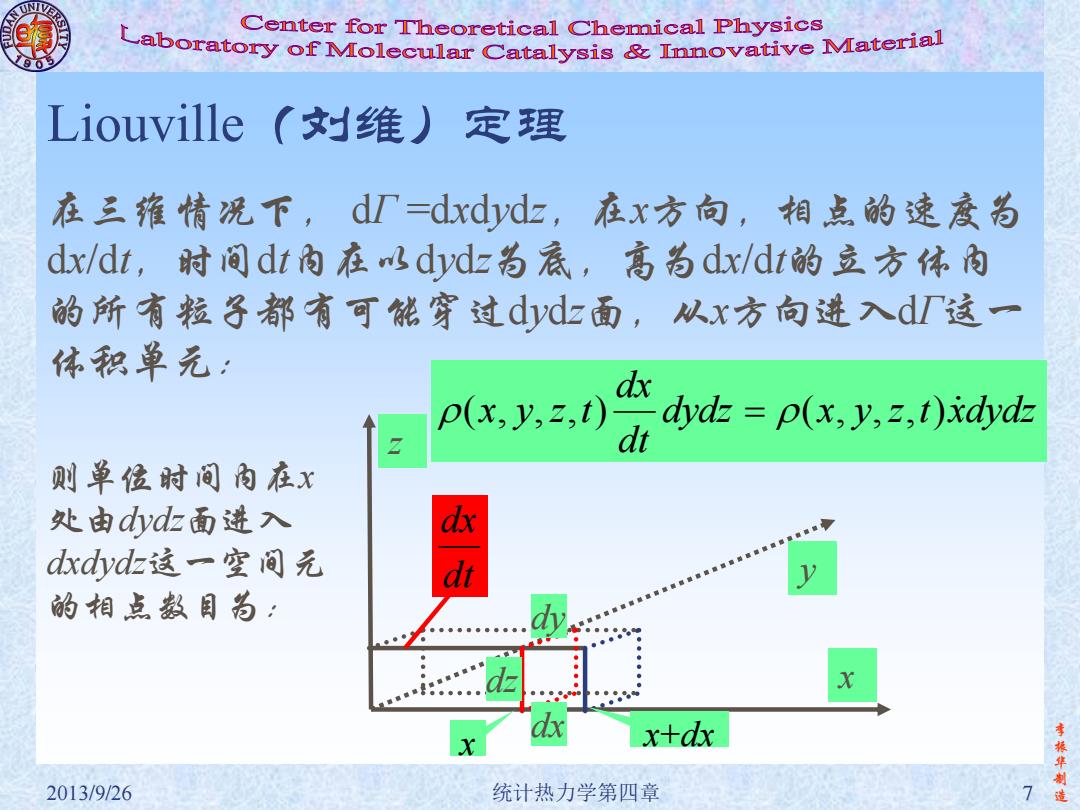
Center for Theoretical Chemical Physics oratory of molecular Catalysis innovative mate Liouville(y维)定理 在三推情况下，d厂=dxdydz,在x方向，相点的速度为 dx/dt,时间dt内在以dydz为底，高为dx/dt的立方体肉 的所有粒子都有可能穿过d山yd面，从x方向进入d厂这一 体积单元： p(x,y,2,t) dydz p(x,y,z,t)xdyd 则单位时间内在x 处由dydz面进入 dx dxdydz这一空间元 1 的相点数目为： 0000年5年00 x+dx 振华制 2013/9/26 统计热力学第四章

李 振 华 制 2013/9/26 统计热力学第四章 7 造 Liouville（刘维）定理 在三维情况下， dΓ =dxdydz，在x方向，相点的速度为 dx/dt，时间dt内在以dydz为底，高为dx/dt的立方体内 的所有粒子都有可能穿过dydz面，从x方向进入dΓ这一 体积单元： dydz x y z t xdydz dt dx (x, y,z,t)  ( , , , )  则单位时间内在x 处由dydz面进入 dxdydz这一空间元 的相点数目为： z y x dx dy dz dt dxx x+dx

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material Liouville(刘维)定理 推广到任意维空间的情况，则单位时间内从g,处的面进入 d厂空间元的相点数目为 p(p.qtqdg dqzdqdqdqdp dpdp 那么在q,+dg,处相点的速度和相密度分别为 op dqi 0qi q:+ qidqi @qi 因此单位时间内从q,+dg,处跑出d空间元的相点数目为 0 op dqi 0qidqi 0qi aqi dqdqdqdqdq dpdp2dp 振华 2013/9/26 统计热力学第四章 8 造

李 振 华 制 2013/9/26 统计热力学第四章 8 造 Liouville（刘维）定理 推广到任意维空间的情况，则单位时间内从qi处的面进入 dΓ空间元的相点数目为 i i i fN fN ( p, q,t)q dq dq ...dq dq ...dq dp dp ...dp 1 2 1 1 1 2   那么在qi+dqi处相点的速度和相密度分别为 i i dq q     i i i i dq q q q      因此单位时间内从qi+dqi处跑出d空间元的相点数目为 i i i fN fN i i i i i dq dq dq dq dq dq dp dp dp q q dq q q ... ... ...  1 2 1 1 1 2                         

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material Liouville(刘维)定理 那么单位时间内在9方向上的相点数变化为： op dqdqdqdpdp 类似地，单位时间内在p,方向上的相点数变化为： Opi dq dqdq dp dpzp 对所有坐标取和，则有 - op OpPi OPi d q: Opi 振华制 2013/9/26 统计热力学第四章 造

李 振 华 制 2013/9/26 统计热力学第四章 9 造 Liouville（刘维）定理 那么单位时间内在qi方向上的相点数变化为： fN fN i i i i q dq dq dq dp dp dp q q q q t N i ... ... ( )  1 2 1 2                            类似地，单位时间内在pi方向上的相点数变化为： 对所有坐标取和，则有 fN fN i i i i p dq dq dq dp dp dp p p p p t N i ... ... ( )  1 2 1 2                                                                       fN i i i i i i i i i p q dΓ p p p p q q q q t N , 1 ( )         

Center for Theoretical Chemical Physics boratory of Molecular Catalysis Innovative Mater Liouville(刘维)定理 则： a(N) q+4i aqi op + p ap D.a opi 注意到： N 三0 dr 代入上式并整理得到： p 0 o ap =0 D.g ap, aqi 李振华 2013/9/26 统计热力学第四章 10 造

李 振 华 制 2013/9/26 统计热力学第四章 10 造 Liouville（刘维）定理 则： 注意到： 0 , 1                                            fN i i i i i i i i i p q p p q q p p q q t         代入上式并整理得到：                                            fN i i i i i i i i i p q p p p p q q q q tdΓ N , 1 ( )             dΓ N