
回H厄✉ Chapter6统计热力学的应用 动力学 化学友应的分子碰撞理论 经典过液态理论 变分过渡态理论 单安子发宝理RM坊法
Chapter 6 统计热力学的应用 动力学 化学反应的分子碰撞理论 经典过渡态理论 变分过渡态理论 单分子反应理论-RRKM方法

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material §6-4反应速率的统计理论 Arrhenius式 k=Ae△Ea/RT △Ea §6-4.1化学反应的碰撞理论 ■分子碰撞的几率 ■有效碰撞(发生反应的几率) 李振华 2015/9/7 统计热力学第六章 2 造
李 振 华 制 2015/9/7 统计热力学第六章 2 造 §6-4 反应速率的统计理论 §6-4.1 化学反应的碰撞理论 分子碰撞的几率 有效碰撞(发生反应的几率) Ea RT k Ae / Arrhenius公式 2 ln R T E T k a p

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 1.分子碰撞的几率 把分子看成球体,半径各为r和r。c为两分子的平均相 对运动速率 d-ra+rB A A 只要分子A处在以d为半径,c为高度的圆柱体中,A在单位时 间内就会和B碰撞,那么可能的碰撞数为 李振华制 2015/9/7 统计热力学第六章 3
李 振 华 制 2015/9/7 统计热力学第六章 3 造 1. 分子碰撞的几率 把分子看成球体,半径各为rA和rB。c为两分子的平均相 对运动速率 A B A A d=rA+rB c 只要分子A处在以d为半径,c为高度的圆柱体中,A在单位时 间内就会和B碰撞,那么可能的碰撞数为

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 单位时间,单位体积内的碰撞次数 NAB=n4nBCπd2 n,和n分别是单位体积内A和B分子的数目,即分子 的数密度。 根据Maxwell-Boltzmann分子速度分布公式,可以求得 1/2 1/2 1/2 8kgT 8(ma+mg)kgT 8(M+MB)RT C 44 rmamB πM4MB 1/2 8π(M4+MB)RT M MB 李振华制 2015/9/7 统计热力学第六章
李 振 华 制 2015/9/7 统计热力学第六章 4 造 单位时间,单位体积内的碰撞次数 nA和nB分别是单位体积内A和B分子的数目,即分子 的数密度。 根据Maxwell-Boltzmann分子速度分布公式,可以求得 2 NAB nA nB cd 1/ 2 1/ 2 1/ 2 8 8( ) 8( ) A B A B A B B A B B M M M M R T m m k T m m k T c 1/ 2 2 8 ( ) A B A B AB A B M M M M R T N n n d

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 同种类分子 如果是同一种类的分子的话,则为上述数目的1/2: 1/2 1/2 2π(M4+MA)RT 4nRT M MA 这样同类分子的反应速率常数就和不同类分子的差 了一倍,因此为了能够把这两类速率常数直接比较, 把同类分子的速率常数一般写为2k,即 不同类分子 dA = k[A][B] di 同类分子 dA = 2k,[A]2 李 dt 华制 2015/9/7 统计热力学第六章
李 振 华 制 2015/9/7 统计热力学第六章 5 造 同种类分子 如果是同一种类的分子的话,则为上述数目的1/2: 这样同类分子的反应速率常数就和不同类分子的差 了一倍,因此为了能够把这两类速率常数直接比较, 把同类分子的速率常数一般写为2k,即 2 2 [ ] [ ][ ] k A dt dA k A B dt dA r r 1/ 2 2 2 1/ 2 2 2 2 ( ) 4 A A A A A A AA A M R T n d M M M M R T N n d 不同类分子 同类分子

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 统一写为: 1/2 NAB nangd2 8π(M4+MB)RT 碰撞数乙AB:如果每一次碰撞都发生反应的话,ZAB 就是反应的速率常数,单位:m3 molecule-1 s-1 1/2 8=d2 8π(MA+MB)RT 、MAMB 李振华 2015/9/7 统计热力学第六章 6 造
李 振 华 制 2015/9/7 统计热力学第六章 6 造 统一写为: 碰撞数ZAB:如果每一次碰撞都发生反应的话,ZAB 就是反应的速率常数,单位:m3 molecule-1 s -1 AB A B A B A B AB A B Z n n M M M M R T N n n d 1/ 2 2 8 ( ) 1/ 2 2 8 ( ) A B A B AB M M M M R T Z d
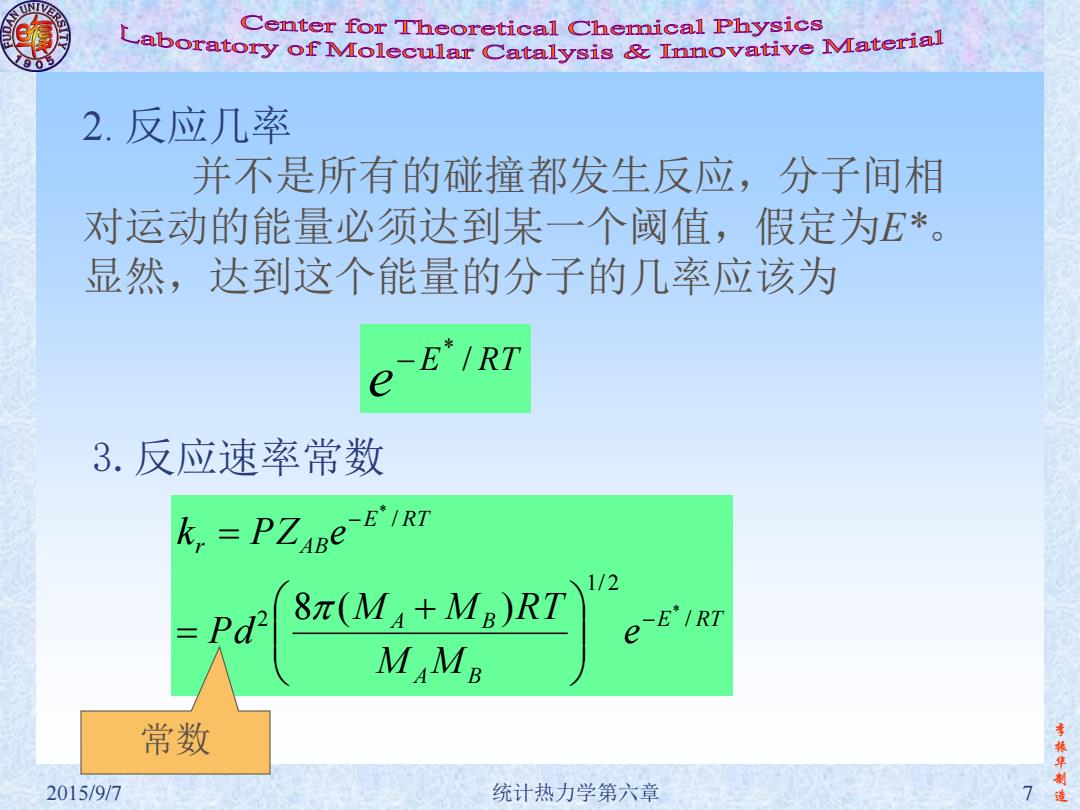
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 2.反应几率 并不是所有的碰撞都发生反应,分子间相 对运动的能量必须达到某一个阈值,假定为E*。 显然,达到这个能量的分子的几率应该为 -E*/RT e 3.反应速率常数 k PZABe-E'IRT 1/2 Pd2 8π(M4+MB)RT e-E'IRT M Mg 常数 李振华 2015/9/7 统计热力学第六章 造
李 振 华 制 2015/9/7 统计热力学第六章 7 造 2. 反应几率 并不是所有的碰撞都发生反应,分子间相 对运动的能量必须达到某一个阈值,假定为E*。 显然,达到这个能量的分子的几率应该为 3.反应速率常数 E RT e / * E RT A B A B E RT r AB e M M M M R T P d k P Z e / 1/ 2 2 / * * 8 ( ) 常数

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 4.碰撞理论的不足 P无法求出 E*无法求出 李振华 2015/9/7 统计热力学第六章 8 造
李 振 华 制 2015/9/7 统计热力学第六章 8 造 4. 碰撞理论的不足 P无法求出 E*无法求出

Center for Theoretical Chemical Physics ratory of Molecular Catalysis Innovative Ma §6-4.2经典过渡态理论 A+BC←→ABC#→AB+C (a+8-C】 20.0 80 16.0 14.0 12.0 10.0 Activated state (ool) -8.0 13 4.0 Q (A-8+C) 19 -2.0 31 -0.0 B-C distance 李振华制 2015/9/7 统计热力学第六章 9
李 振 华 制 2015/9/7 统计热力学第六章 9 造 §6-4.2 经典过渡态理论 A+BCABC#AB+C 1 7 13 19 25 31 37 S1 S3 S5 S7 S9 S11 S13 S15 S17 S19 S21 S23 S25 S27 S29 S31 0.0 2.0 4.0 6.0 8.0 10.0 12.0 14.0 16.0 18.0 20.0

Center for Theoretical Chemical Physics pratory of molecular Catalysis innovative mat §6-4.2经典过渡态理论 实验上已经可以用超快光谱(s技术)直接观测过渡态 1.Manolopoulos,D.E.;Stark,K.; Werner,H.J.;Arnold,D.W.;Bradforth. S.E.;Neumark,D.M.Science,1993. 262(5141),1852:F+H 2.Dmello,M.J.;Manolopoulos,D.E.; F+H Wyatt,R.E.Science,1993,263(5143). 102:H+D2 李振华 2015/9/7 统计热力学第六章 10 造
李 振 华 制 2015/9/7 统计热力学第六章 10 造 §6-4.2 经典过渡态理论 实验上已经可以用超快光谱(fs技术)直接观测过渡态 1. Manolopoulos, D. E.; Stark, K.; Werner, H. J.; Arnold, D. W.; Bradforth, S. E.; Neumark, D. M. Science, 1993, 262(5141), 1852: F+H2 2. Dmello, M. J.; Manolopoulos, D. E.; Wyatt, R. E. Science, 1993, 263(5143), 102: H+D2