
Chapter7 Monte Carlo.及相关方法 §7.1 Monte Carlo模拟 §7.2分子动力学模拟
Chapter 7 Monte Carlo及相关方法 §7.1 Monte Carlo模拟 §7.2 分子动力学模拟

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material §7.2 Molecular Dynamics(分子动力学)模 拟 与Monte Carlo摸拟的区别: Monte Carlo模拟中,分子坐标的改变是完全随 机的,跟分子所受的力毫无关系 分子力学中,根据力的大小和方向来决定移动 的方向 中心问题:解牛顿运动方程,得到分子坐标和速度 是如何随时间而改变的(轨迹,trajectory) F=m,d F= q4= dyd'x dt dt dt2 李振华制 10/14/2013 第七章-2MD方法
李 振 华 制 10/14/2013 第七章-2 MD 方法 2 造 §7.2 Molecular Dynamics (分子动力学)模 拟 与Monte Carlo模拟的区别: Monte Carlo模拟中,分子坐标的改变是完全随 机的,跟分子所受的力毫无关系 分子力学中,根据力的大小和方向来决定移动 的方向 中心问题:解牛顿运动方程,得到分子坐标和速度 是如何随时间而改变的(轨迹,trajectory) Fi mi ai dt dp F i i 2 2 dt d x dt dv a i i i

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material §7.2-1MD的简单模型 硬球摸型(Alder and Wainwright in1957): ■粒子作匀速直线运动,直到它碰撞到其它粒子 粒子间的相互作用只有在粒子的相互距离小于 其半径之和时才存在: distance 李振华制 10/14/2013 第七章-2MD方法 3
李 振 华 制 10/14/2013 第七章-2 MD 方法 3 造 §7.2-1 MD的简单模型 硬球模型(Alder and Wainwright in 1957): 粒子作匀速直线运动,直到它碰撞到其它粒子 粒子间的相互作用只有在粒子的相互距离小于 其半径之和时才存在: U distance

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material §7.2-1MD的简单模型,continue ■硬球模型粒子间的相互作用的小改进: distance 李振华 10/14/2013 第七章-2MD方法 4 造
李 振 华 制 10/14/2013 第七章-2 MD 方法 4 造 §7.2-1 MD的简单模型,continue 硬球模型粒子间的相互作用的小改进: U distance
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material §7.2-1MD的简单模型,continue 硬球模型的模 按速率分布随机给出 拟步骤: 初始的位置和速度 计算下一次碰撞时间 计算碰撞时的位置 根据动量守恒定律计 算碰撞后的新速度 是否继续 Analyze Output 李振华 10/14/2013 第七章-2MD方法 5 造
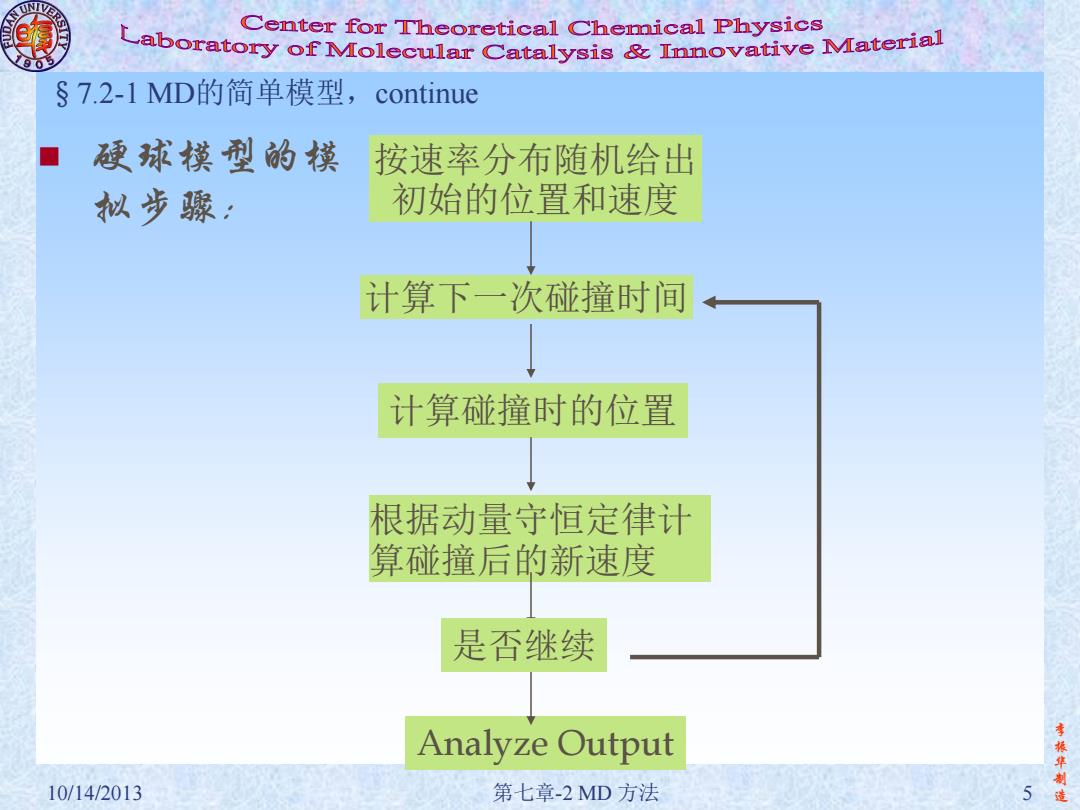
李 振 华 制 10/14/2013 第七章-2 MD 方法 5 造 §7.2-1 MD的简单模型,continue 硬球模型的模 拟步骤: 按速率分布随机给出 初始的位置和速度 计算碰撞时的位置 根据动量守恒定律计 算碰撞后的新速度 Analyze Output 是否继续 计算下一次碰撞时间

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material §7.2-2使用连续势能函数的MD 作用在分子或粒子上的力其实是时刻在改变的 无法求解N个粒子的运动方程,因此采用其它法求 解运动方程 l.有限差分方法(Finite Difference Methods) 时间t的状态(速度,位置)是通过把0-t的积分分 为很小的时间间隔t的运动的加和,假定粒子在这 段很短的时间间隔之内受到的力是常数 李振华制 10/14/2013 第七章-2MD方法 6
李 振 华 制 10/14/2013 第七章-2 MD 方法 6 造 §7.2-2 使用连续势能函数的MD 作用在分子或粒子上的力其实是时刻在改变的 无法求解N个粒子的运动方程,因此采用其它法求 解运动方程 1.有限差分方法(Finite Difference Methods) 时间t的状态(速度,位置)是通过把0-t的积分分 为很小的时间间隔δt的运动的加和,假定粒子在这 段很短的时间间隔之内受到的力是常数

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mmnovative Material 有限差分方法(Finite Difference Methods) 假定粒子在某时刻附近的位置和速度可以用Taylor 阶数展开: rt+0)=r0)+v06d+)a0o2+2b(0)6x2+c0)4+ 2 6 24 (+)v()) 2 a(t+)=a(t)+b(t)ot+。c(t)62+… b(t+ot)=b(t)+c(t)ot+... 振华 10/14/2013 第七章-2MD方法 造
李 振 华 制 10/14/2013 第七章-2 MD 方法 7 造 有限差分方法(Finite Difference Methods) 假定粒子在某时刻附近的位置和速度可以用Taylor 阶数展开: t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t ( ) ( ) ( ) ( ) 2 1 ( ) ( ) ( ) ( ) 6 1 ( ) 2 1 ( ) ( ) ( ) ( ) 24 1 ( ) 6 1 ( ) 2 1 ( ) ( ) ( ) 2 2 3 2 3 4 b b c a a b c v v a b c r r v a b c

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mvative Material 有限差分方法(Finite Difference Methods) ■ Verlet算法: 利用t-δt的位置r(t-t)和t时刻的位置r(t)和加速度 a(t)计算什δt的位置r(t什δt) r(t+)=r(t)+v(t)m+a(t)62+. 2 rt-0)=r0-ox+2a0x+… r(t+ot)=2r(t)-r(t-6t)+a(t)ot2 李振华 10/14/2013 第七章-2MD方法 8 造
李 振 华 制 10/14/2013 第七章-2 MD 方法 8 造 有限差分方法(Finite Difference Methods) Verlet算法: 利用t-δt的位置r(t-δt)和t时刻的位置r(t)和加速度 a(t)计算t+δt的位置r(t+δt) 2 2 ( ) 2 1 ( ) ( ) ( ) ( ) 2 1 ( ) ( ) ( ) t t t t t t t t t t t t t t r r v a r r v a 2 r(t t) 2r(t) r(t t) a(t)t

Center for Theoretical Chemical Physics boratory of Molecular Catalysis Innovative Materi 有限差分方法(Finite Difference Methods) Verlet算法一速度 ■最简单的方法 V()= r(t+ot)-r(t-ot) 26d ■也可以计算half-step(t什l/2t)的速度 vt+0= r(t+8t)-r(t) 2 St 李振华 10/14/2013 第七章-2MD方法 9 造
李 振 华 制 10/14/2013 第七章-2 MD 方法 9 造 有限差分方法(Finite Difference Methods) Verlet算法——速度 最简单的方法 t t t t t t 2 ( ) ( ) ( ) r r v 也可以计算half-step (t+1/2δt)的速度 t t t t t t ( ) ( ) ) 2 1 ( r r v

Center for Theoretical Chemical Physics Laboratory of molecular Catalysis Innovative material 有限差分方法(Finite Difference Methods) ,Verlet.算法—FORTRAN 77程序 do i=1.natoms do j=1,3 C Integrate on coordinates r(t+)=2r(t)-r(t-6)+a(t)62 xt=2.d0*xxm(j,i)-xp(j,i)-dt*dt gv(j,i)/m(i) C update momentum r(t+)-r(t-) ppm(j,i)=m(i)*(xt -xp(j,i))/(2.d0*dt) v()= C 26 save current y as yp xp(j,i)=xxm(j,i) C save new x (xt xxm(j,i)=xt enddo enddo 振华 10/14/2013 第七章-2MD方法 10造
李 振 华 制 10/14/2013 第七章-2 MD 方法 10 造 有限差分方法(Finite Difference Methods) Verlet算法——FORTRAN 77程序 do i=1,natoms do j=1,3 C Integrate on coordinates xt = 2.d0*xxm(j,i) - xp(j,i) - dt*dt * gv(j,i)/m(i) C update momentum ppm(j,i) = m(i) * (xt - xp(j,i)) / (2.d0*dt) C save current y as yp xp(j,i) = xxm(j,i) C save new x ( xt ) xxm(j,i) = xt enddo enddo 2 r(t t) 2r(t) r(t t) a(t)t t t t t t t 2 ( ) ( ) ( ) r r v