
e包回H厄与 第八章 方差分析 (Analysis of Variance)简称ANOVA
数理统计在化学中的应用 第八章 方差分析 (Analysis of Variance)简称ANOVA

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 方差分析 在化学中,对一个试样进行分折或进行一个化学反 寇时,常常要选掉具体的实验条件,通常需要通过多 次条件试验才能确定。这种条件试脸何进行?其 结果能说明什么间题?这就要借助于方差分析来给出 解答。 Ronald A.Fisher开发异首先寇用了方差分折作筒 实验被计中的设计分折的基李方法. 李 华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 方差分析 在化学中,对一个试样进行分析或进行一个化学反 应时,常常要选择具体的实验条件,通常需要通过多 次条件试验才能确定。这种条件试验应如何进行?其 结果能说明什么问题?这就要借助于方差分析来给出 解答。 Ronald A. Fisher开发并首先应用了方差分析作为 实验设计中的设计分析的基本方法

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material $8.1化学试验的单因素方差分析 单因素方差分折,是指仅分折一个因章对试验猪果 的影响是香显著的问题。例品,在分析化学中实验 被分折喀液的酸意对分折猪果的影响是香显著。 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 $8.1 化学试验的单因素方差分析 ◼ 单因素方差分析,是指仅分析一个因素对试验结果 的影响是否显著的问题。例如,在分析化学中实验 被分析溶液的酸度对分析结果的影响是否显著
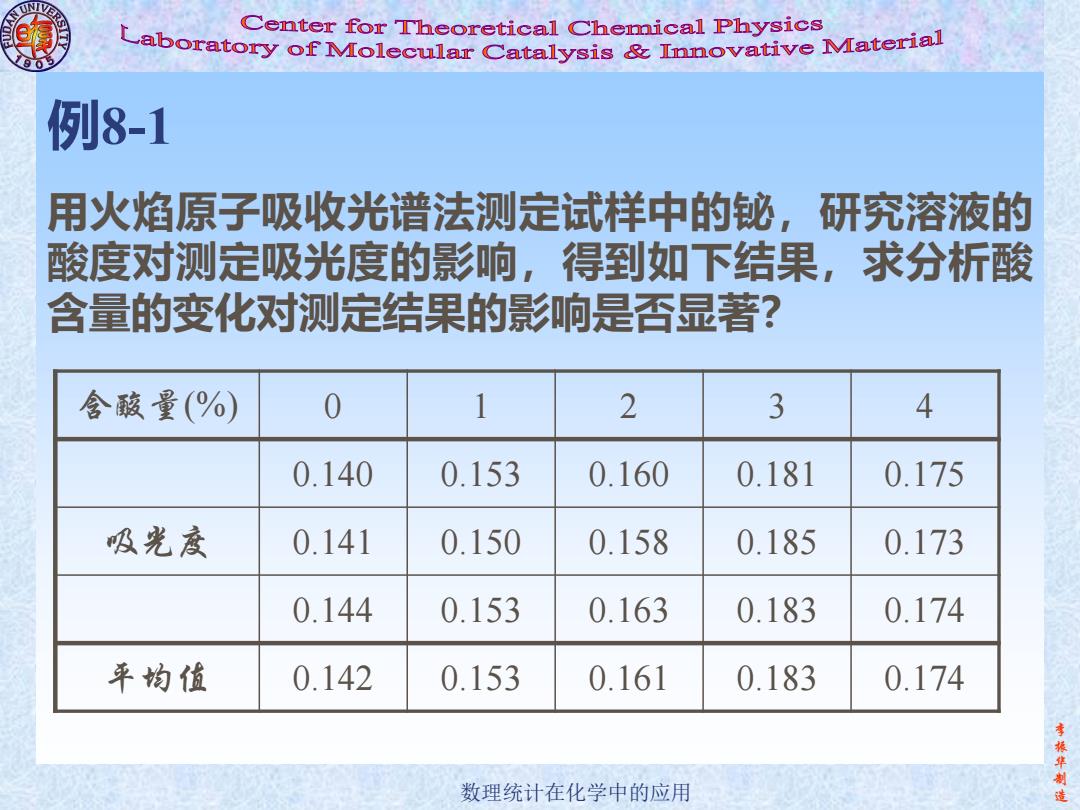
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 90 例8-1 用火焰原子吸收光谱法测定试样中的铋,研究溶液的 酸度对测定吸光度的影响,得到如下结果,求分析酸 含量的变化对测定结果的影响是否显著? 含酸量(%) 0 1 2 3 4 0.140 0.153 0.160 0.181 0.175 吸光度 0.141 0.150 0.158 0.185 0.173 0.144 0.153 0.163 0.183 0.174 平均值 0.142 0.153 0.161 0.183 0.174 振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 例8-1 用火焰原子吸收光谱法测定试样中的铋,研究溶液的 酸度对测定吸光度的影响,得到如下结果,求分析酸 含量的变化对测定结果的影响是否显著? 含酸量(%) 0 1 2 3 4 0.140 0.153 0.160 0.181 0.175 吸光度 0.141 0.150 0.158 0.185 0.173 0.144 0.153 0.163 0.183 0.174 平均值 0.142 0.153 0.161 0.183 0.174

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 在方差分折中,把所有数据之间的差异叫徵总变差。 产生总变差的原因有面美,一美是条件变差(本例中 即是酸度的影响),另一美就是试验误差。方差分析 解决这个间题的办法就是: 1、从总变差中区分出试验变差和条件变差,也就 是将不同因素的影响给区分开来。 2、利用F检验比较这两个变差的大小,确定出主 要变差。 3、根据主要的变差,去选择较好的分析条件,或 确定进一步试验的方向。 李振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 在方差分析中,把所有数据之间的差异叫做总变差。 产生总变差的原因有两类,一类是条件变差(本例中 即是酸度的影响),另一类就是试验误差。方差分析 解决这个问题的办法就是: 1、从总变差中区分出试验变差和条件变差,也就 是将不同因素的影响给区分开来。 2、利用F检验比较这两个变差的大小,确定出主 要变差。 3、根据主要的变差,去选择较好的分析条件,或 确定进一步试验的方向

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 方差分析的基本思想 方差分析的依据是建立在变差平方和具有加和性的 基础上的。因此,如果用变差平方和来表征测定猪 果的总变差,那么总变差的平方和就等于各变异因 素形成的变差平方和的总和。 方差分析的基本思想,就是将总变差分解为各构成 部分之和,然后对它们作统计检验。总变差: SS=∑∑(X,-)2 i=1i=1 其中m为试验水平数,n为重复次数,自由度vT= mn-1=W-1 振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 方差分析的基本思想 ◼ 方差分析的依据是建立在变差平方和具有加和性的 基础上的。因此,如果用变差平方和来表征测定结 果的总变差,那么总变差的平方和就等于各变异因 素形成的变差平方和的总和。 ◼ 方差分析的基本思想,就是将总变差分解为各构成 部分之和,然后对它们作统计检验。总变差: 其中m为试验水平数,n为重复次数,自由度vT = mn – 1 = N – 1 2 1 1 ( ) m n T ij i j SS X X = = = −

Center for Theoretical Chemical Physics Laboratory of molecular Catalysis innovative material 9 条件变差(组间方差) 每一组的测定平怕值和总平怕值差值的平方和再乘 以重复次数 SS4=n(,-)} i1 自由度vA=m-1 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 条件变差(组间方差) ◼ 每一组的测定平均值和总平均值差值的平方和再乘 以重复次数: 自由度vA = m – 1 2 1 ( ) m A i i SS n X X = = −

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 试验误差(组内方差) ■各组内的每次测定值和组内平怕值差值的平方和: 177 SS=∑∑(X,-,)》月 i=1j=1 自由度ye=m(n-1)=N-m 李振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 试验误差(组内方差) ◼ 各组内的每次测定值和组内平均值差值的平方和: 自由度ve = m(n – 1) = N – m 2 1 1 ( ) m n e ij i i j SS X X = = = −

Center for Theoretical Chemical Physics Laboratory of molecular Catalysis innovative material 总变差的分解 5S4=n2(区,-X2 5S.=∑∑(X,-x,) 1= i=1 j=1 SS,=∑∑(X,-x=∑∑(X,-,)+(,-X i- =∑2(X,-)2+∑∑(,-+2∑∑(X,-X,x,-) i=1j=1 i=1 i=l i=1 i=l 22X,-+(x-X+2(,-x,-,) i=1j=1 i=1 i=1 SS,=∑∑(X,-X,)+22(元,-X i=1 i=1 i=l =SS4+SS。 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 总变差的分解 2 1 ( ) m A i i SS n X X = = − 2 2 1 1 1 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1 1 1 ( ) [( ) ( )] ( ) ( )] 2 ( )( ) ( ) ( ) 2 ( ) ( ) m n m n T ij ij i i i i i j m n m n m n ij i i ij i i i j i j i j m n m n m n ij i i i ij i i j i j i j SS X X X X X X X X X X X X X X X X X X X X X X = = = = = = = = = = = = = = = = = − = − + − = − + − + − − = − + − + − − 2 2 1 1 1 1 ( ) ( )] m n m n T ij i i i j i j A e SS X X X X SS SS = = = = = − + − = + 2 1 1 ( ) m n e ij i i j SS X X = = = −
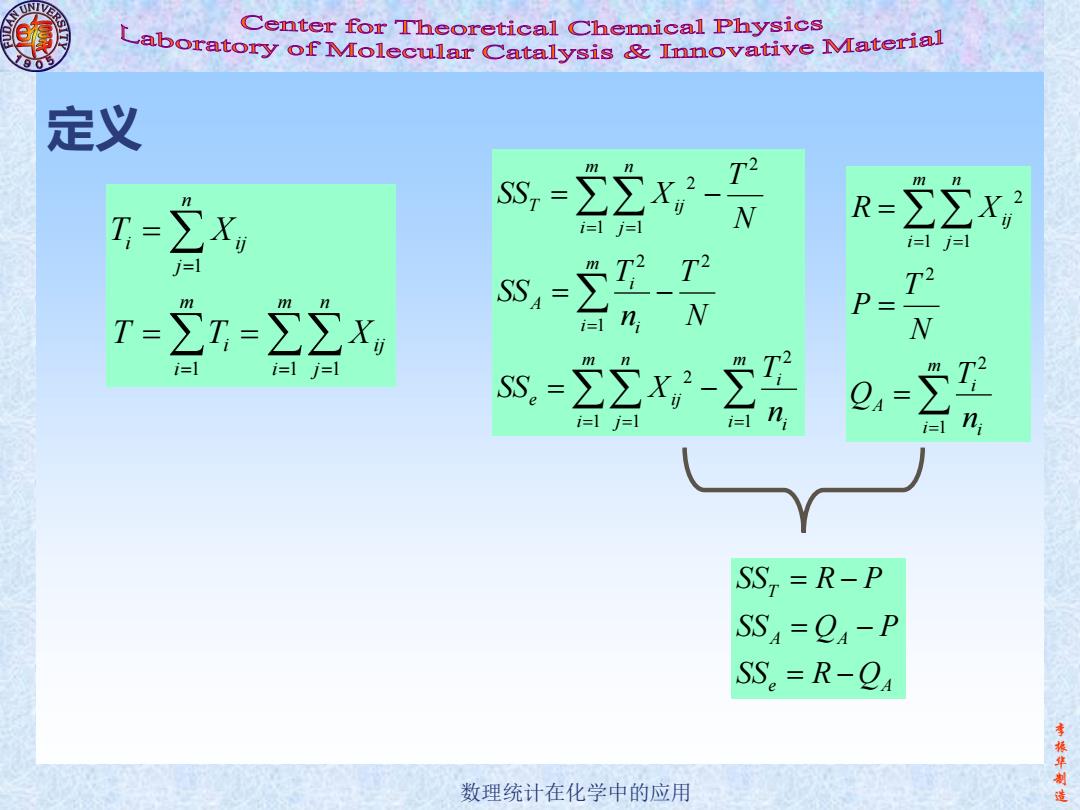
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 定义 n I=∑x, i=1 j=1 N R= ∑∑x, i=1 i=l r-,=22x, s,- 2_ P= i=l n N i=1i= 拉网 4= i=1 j=1 i=l 得 SS,=R-P SS=O4-P SS。=R-Qa 数理统计在化学中的应用 李振华制造
李 振 华 制 数理统计在化学中的应用 造 定义 1 1 1 1 n i ij j m m n i ij i i j T X T T X = = = = = = = 2 2 1 1 2 2 1 2 2 1 1 1 m n T ij i j m i A i i m n m i e ij i j i i T SS X N T T SS n N T SS X n = = = = = = = − = − = − 2 1 1 2 2 1 m n ij i j m i A i i R X T P N T Q n = = = = = = T A A e A SS R P SS Q P SS R Q = − = − = −