第八讲:多原子分子 价键理论与杂化轨道
第八讲:多原子分子 价键理论与杂化轨道

价键理论与杂化轨道 1.H分子的VB理论 1).S方程 1* R, 2 Hw(1,2)=Ew(1,2) al a2 R a b 2).价键理论观点 原子=原子实+价电子,价电子自旋配对,形成化学键 整体波函数=空间波函数×自旋波函数,满足交换反对称 >2
a b 1 2 a1 r a2 r b1 r b2 r R H E 1, 2 1, 2 0 0 12 1 2 2 2 1 2 1 2 2 1 12 1 1 1 1 1 111 2 2 a b ab V H H H r r r r Rr 1 44 2 4 43 1 44 2 4 43 1442443 = + = 原子 原子实 价电子,价电子自旋配对,形成化学键 整体波函数 空间波函数 自选波函数,满足交换反对称 2 价键理论与杂化轨道 1). S方程 2). 价键理论观点 1.H2分子的VB理论 自旋

价键理论与杂化轨道 1.H2分子的VB理论 3).波函数:空间部分(2电子) R→o时,无相互作用,=ls(1)1s(2),4,=1s(2)1s6(1) 线性组合:p(1,2)=c4+c24,=cls.(1)1s,(2)+c21s.(2)1s(1) G,c,可由线性变分法求得 线性变分,易得波函数如下: 2)2容质+.=32传- 其中,S为重叠积分(与MO一致) 下标S:交换对称;A:交换反对称 S=1s.()川1s,(1)》=∫1s,()1s,()dw >3
12 12 2 2 1 1 1, 2 , 22 22 s A S S 线性变分,易得波函数如下: 1 MO 1 |1 1 1 1 1 1 a b ab S S s s s s dv 其中, 为重叠积分 与 一致 下标S: 交换对称; : 交换反对称 A 3 价键理论与杂化轨道 R ss s s 时,无相互作用, 1 2 =1 1 1 2 , 1 2 1 1 ab a b 11 2 2 1 2 1 2 1, 2 1 1 1 2 1 2 1 1 , ab a b c c cs s c s s c c 线性组合: 可由线性变分法求得 1.H2分子的VB理论 3). 波函数: 空间部分(2电子)

价键理论与杂化轨道 1.H2分子的VB理论 3).波函数:自旋部分 问题:两个电子组合的总波函数? 2电子组合,按角动量耦合规则,总自旋量子数S=1,0 可能的状态组合ax(1)a(2),B(1)B(2),ax()B(2),ax(2)B(1) n=a()a(2)与n2=B()B(2)均满足交换对称性 而α(1)B(2)与a(2)B()均不满足交换对称性,可进行线性组合: -交换对称:n=[a()B(2)+a(2)B()]/2 -交换反对称:n4=[a()B(2)-a(2)B()]/N2 *可以证明:n,n2,n,n4均是5及$2的本征函数 S.n4=0,§n=+an,n2--An9,2n月=0 2n4=0,2n9=2A2n9,S2n2=22n2,S2n月=2A2n >4 其中,§.=5+$2=(,+)=(++2(S5+5,+5)》
问题:两个电子组合的总波函数? 1 0 12 12 12 21 S 2电子组合,按角动量耦合规则,总自旋量子数 , 可能的状态组合 , , , 1 2 3 12 12 12 21 -- 1 2 + 2 1 2 -- 1 2 2 1 2 S S S A 与 均满足交换对称性 而 与 均不满足交换对称性,可进行线性组合: 交换对称: 交换反对称: 4 价键理论与杂化轨道 3). 波函数: 自旋部分 1.H2分子的VB理论 123 2 ˆ ˆ * ,,, ss s A z 可以证明: 均是 及 的本征函数 S S 2 2 22 1 2 1 2 1 2 12 12 12 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆˆ ˆˆ ˆˆ , 2 z z z xx yy zz 其中,S S S S S S S S SS SS SS 2 2 22 22 2 1 1 2 23 3 ˆ ˆ ˆ ˆ 0, 2 , 2 , 2 A S SS SS S SS S S hhh 1 12 2 3 2 ˆˆ ˆ ˆ 0, , , 0; zA zS S zS S S SS S S h h
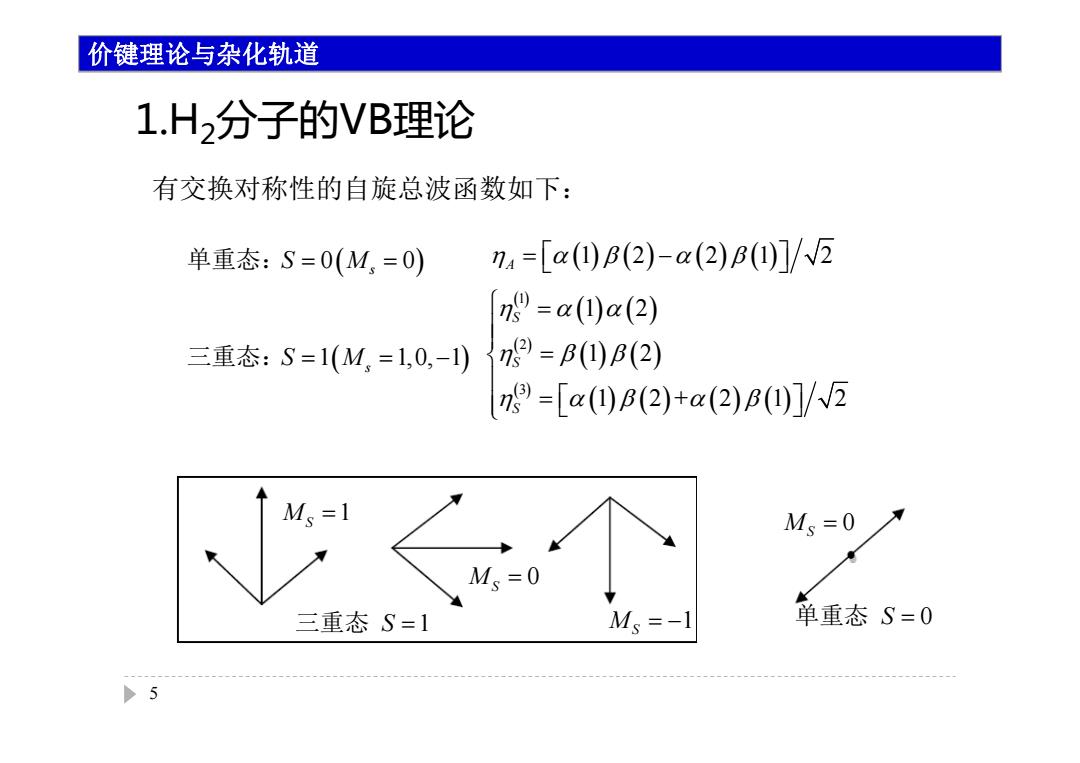
价键理论与杂化轨道 1.H2分子的VB理论 有交换对称性的自旋总波函数如下: 单重态:S=0(M,=0) na=[a(四)B(2)-a(2)B()]/N2 n=a()a(2) 三重态:S=1(M,=1,0,-1)n2=B()B(2) n=[a()B(2)+a(2)B()]/2 M3=1 个 Ms=0 三重态S=1 Ms=-1 单重态S=0
有交换对称性的自旋总波函数如下: 单重态:S M 0 0 s 三重态:S M 1 1, 0, 1 s A 12 21 2 1 2 3 1 2 1 2 1 2+ 2 1 2 S S S 三重态 S 1 单重态 S 0 1 M S 0 M S 1 M S 0 M S 5 价键理论与杂化轨道 1.H 2分子的VB理论
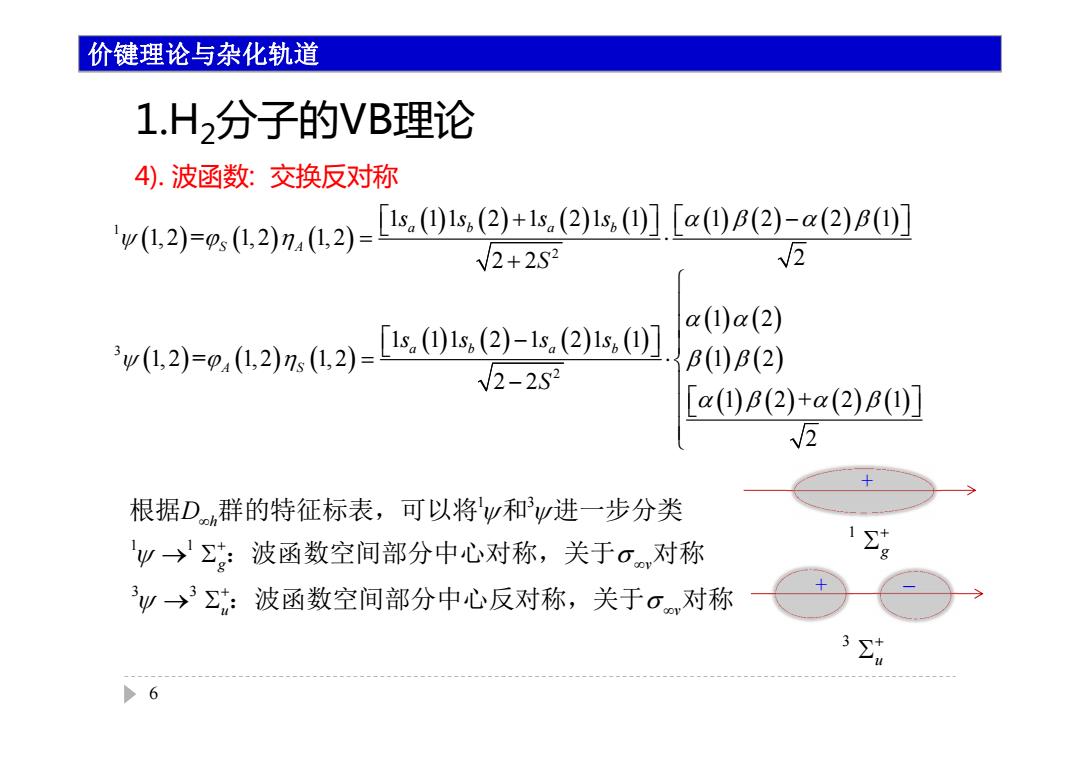
价键理论与杂化轨道 1.H2分子的VB理论 4).波函数:交换反对称 'w(L,2)=RL2到7.0.2)-L.01s,2)+1.(2,].[0B2)-a2B0 V2+2S2 √2 y0,2=p,L2.L2=ls⑨1s2)-1s.21s,] a()a(2) B(1B(2) V2-2S2 [a()B(2)+a(2)B(0)] √2 根据D群的特征标表,可以将w和w进一步分类 w→:波函数空间部分中心对称,关于o对称 12 W→3:波函数空间部分中心反对称,关于o对称 3 >6
1 2 1 11 2 1 21 1 1 2 2 1 1, 2 = 1, 2 1, 2 2 2 2 ab a b S A ss s s S 3 2 1 2 1 11 2 1 21 1 1, 2 = 1, 2 1, 2 1 2 2 2 1 2+ 2 1 2 ab a b A S ss s s S 1 3 1 1 3 3 h g v u v D 根据 群的特征标表,可以将 和 进一步分类 :波函数空间部分中心对称,关于 对称 :波函数空间部分中心反对称,关于 对称 + + - 1 g 3 u 6 价键理论与杂化轨道 1.H2分子的VB理论 4). 波函数: 交换反对称
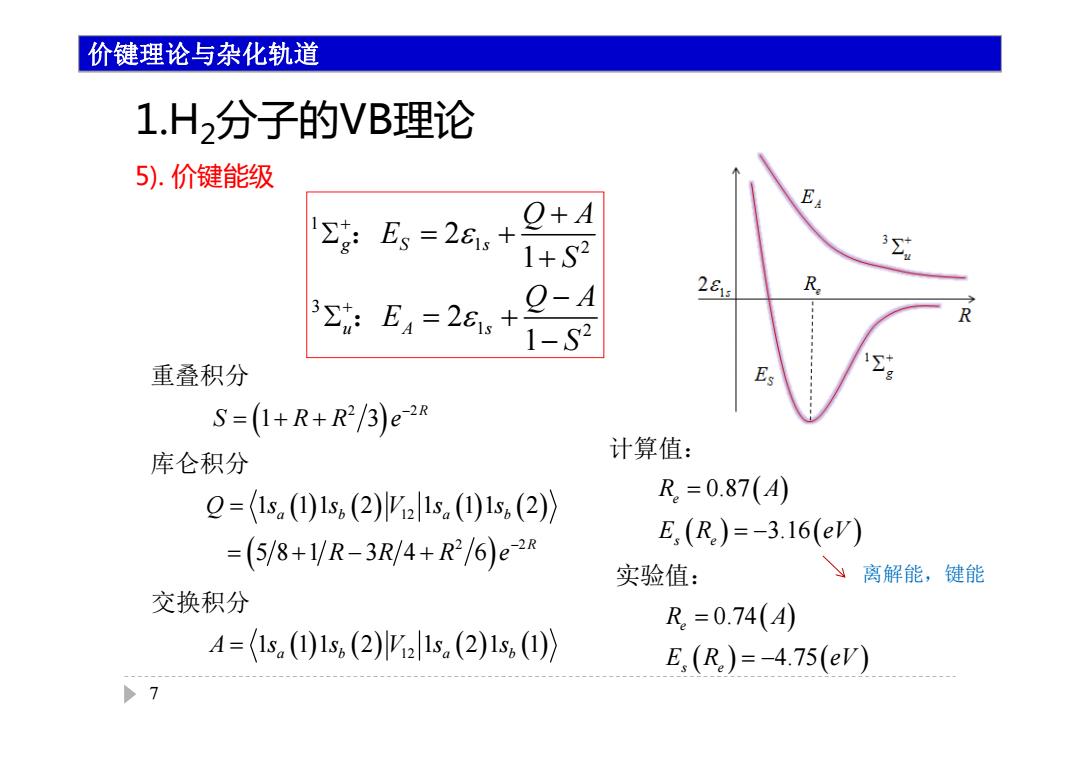
价键理论与杂化轨道 1.H2分子的VB理论 5).价键能级 2:E、=26.+ Q+A 1+S2 3 3:E4=26,+ Q-A 281 R R 1-S2 重叠积分 Es S=(1+R+R2/3)e2R 库仑积分 计算值: Q=(1s.()1s(2)l2l1s.()1s.(2)》 R=0.87(A) =(5/8+VR-3R/4+R2/6)e2R E,(R)=-3.16(e) 实验值: 离解能,键能 交换积分 R=0.74(A) A=1s,(1s,(2)lΨ2l1s.(2)1s,(()》 E,(R)=-4.75(e) >7
1 1 2 3 1 2 2 1 2 1 gS s uA s Q A E S Q A E S : : 2 2 1 3 R S RR e 重叠积分 12 2 2 1 11 2 1 11 2 58 1 3 4 6 ab ab R Q s s Vs s RR R e 库仑积分 A s s Vs s 1 11 2 1 21 1 ab a b 12 交换积分 0.87 3.16 e s e R A E R eV 计算值: 0.74 4.75 e s e R A E R eV 实验值: 离解能,键能 7 价键理论与杂化轨道 1.H 2分子的VB理论 5). 价键能级

价键理论与杂化轨道 1.H2分子的VB理论 6).比较MO对H2的处理 4g((1,2)= 1s()1,(2)+1s(2)1s,()][a()B(2)-a(2)B() V2+2S2 2 按MO理论,H的基态为1o.,总电子波函数为 L2)方e,0 11og()a()log(2)a(2) )1o.(2)B(2) 自旋部分相同,单重态 =lo,()1o,(2).a0P(2)-a(2)P √2 其中,1o为同核双原子分子轨道:1o:@=5[5,()+1s,] a因-,m →B:(HH) →()) →波函数对称性与自旋态均相同,空间轨道成分有差异 >8
1 1 11 2 1 21 1 1 11 2 2 2 1 1 1 2 +1 1 1 2 ab a b g g aa bb ss s s S ss ss 2 MO 1 , H2 g 按 理论, 的基态为 总电子波函数为 MO 1 1 1 11 2 2 1, 2 2 1 1 11 2 2 12 21 1 11 2 2 g g g g g g 1 1 1 1 1 1 +1s 1 2 g g ab s 其中, 为同核双原子分子轨道: 1 2 1 11 2 1 21 1 1 2 2 1 1, 2 = 2 2 2 ab a b VB ss s s S 自旋部分相同,单重态 VB :H H + H H 波函数对称性与自旋态均相同,空间轨道成分有差异 8 6). 比较MO对H2的处理 价键理论与杂化轨道 1.H2分子的VB理论

价键理论与杂化轨道 1.H2分子的VB理论 7).价键理论要点 两原子相互靠近,各提供1个未配对价电子(也可是配键),形成共价键 ·两电子自旋反平行配对,成键波函数为自旋单重态 w2-2+2s0aar6a00AeaO)e0 √2 ·价键理论是局域键模型,共价键类型可分为σ与π键等 价键理论能说明共价键的饱和性与方向性 不能解释O,有顺磁性(未配对电子数为0)的事实,需要用MO 为了解释未配对电子数不够及分子构型问题,需引入杂化的概念 >9
1 2 2 1 • 1 12 21 1, 2 1 2 2 1 2 2 2 • MO ab a b S O 两原子相互靠近,各提供 个未配对价电子(也可是配键),形成共价键 两电子自旋反平行配对,成键波函数为自旋单重态 价键理论是局域键模型,共价键类型可分为 与 键等 价键理论能说明共价键的饱和性与方向性 不能解释 有顺磁性(未配对电子数为0)的事实,需要用 为了解释未配对电子数不够及分子构型问题,需引入杂化的概念 9 价键理论与杂化轨道 1.H2分子的VB理论 7). 价键理论要点

价键理论与杂化轨道 2.杂化轨道理论 1).理论要点 能量相近的原子轨道混合,匹配价电子数和分子构型 {}→p.=∑4c4 Origin of sp3 hybrid orbitals p不是原子的本征函数 atomics 对分子点群,如CH,的T,群 orbital three atomic p orbitals (PyPz) {.4}可按不可约表示分类 Atom with hybridized orbitals hybridize (the hybrid orbitals are shown slightly displaced away from the {p。.4}形成可约表示的基 center for clarity.In the actual molecule,the minor lobes of the hybrid orbitals are centered four sphybrid orbitals in here.) tetrahedral configuration 可由此判断参与杂 化的原子轨道种类 常见杂化类型 p.(p,p,p),dsp2,pd,p2d(dp) >10
2.杂化轨道理论 能量相近的原子轨道混合,匹配价电子数和分子构型 k kk k c 不是原子的本征函数 2 3 2 3 23 2 3 , , , , , ,... n sp sp sp sp dsp sp d sp d d sp 常见杂化类型 可由此判断参与杂 化的原子轨道种类 4 1,...,4 =1,...,4 d k CH T 对分子点群,如 的 群 可按不可约表示分类 形成可约表示的基 10 价键理论与杂化轨道 1). 理论要点