第九讲:多原子分子 金属配合物晶体场理论
第九讲:多原子分子 金属配合物晶体场理论

金属配合物晶体场理论 1.金属配合物 1).历史 ML,:金属离子或原子与它周围n个离子或分子形成的化合物 例如[Fe(H0)6]3+ 价键理论(VB) 配合物的中央离子(或原子)和配位体之间的化学键可分为电价配键和共价 配键两种。 电价配合物,带正电的中心离子和带负电或具有偶极矩的配位体之间是 靠静电引力结合成键,呈高自旋状态。 共价配合物,配位体的孤对电子和中心离子空的杂化价轨道形成共价配 键,呈低自旋状态。 价键理论说明了高自旋配合物和低自旋配合物产生的原因,对配合物的 磁性和几何构型也都给予了一定的说明。但作为一个定性的理论,价键 理论有很大的局限性。 >2
1. 金属配合物 2 MLn : 金属离子或原子与它周围 n 个离子或分子形成的化合物 价键理论(VB) 例如 [Fe( H2O )6]3+ 配合物的中央离子(或原子)和配位体之间的化学键可分为电价配键和共价 配键两种。 电价配合物,带正电的中心离子和带负电或具有偶极矩的配位体之间是 靠静电引力结合成键,呈高自旋状态。 共价配合物,配位体的孤对电子和中心离子空的杂化价轨道形成共价配 键,呈低自旋状态。 价键理论说明了高自旋配合物和低自旋配合物产生的原因,对配合物的 磁性和几何构型也都给予了一定的说明。但作为一个定性的理论,价键 理论有很大的局限性。 金属配合物晶体场理论 1). 历史

金属配合物晶体场理论 1.金属配合物 晶体场(CFT) 1929年,H.Bethe用量子力学结合群论初步建立了晶体场方法。 1932年,van Vleck在Bethe的工作基础上,提出过渡金属配合物 的化学键理论,较好地解释金属配合物的磁性和稳定性。 分子轨道法(MO) 将配合物视为一个大的分子,用MO法处理。因包含金属d轨道, MO成分较为复杂。在MO法中,对称性匹配原侧是关键因素。 1950年代以后,人们吸收上述理论的优点,发展了配位场理论。 >3
3 晶体场(CFT) 分子轨道法(MO) 1929年,H. Bethe 用量子力学结合群论初步建立了晶体场方法。 将配合物视为一个大的分子,用MO法处理。因包含金属 d 轨道, MO成分较为复杂。在MO法中,对称性匹配原则是关键因素。 1950年代以后,人们吸收上述理论的优点,发展了配位场理论。 1932年,van Vleck 在Bethe的工作基础上,提出过渡金属配合物 的化学键理论,较好地解释金属配合物的磁性和稳定性。 1. 金属配合物 金属配合物晶体场理论

5.3金属配合物晶体场理论 2.晶体场理论 1)、基本思想 金属配合物的成键类似于离子晶体中正负离子的作用。 ()金属与配体的作用为静电作用,配体视为点电荷。 (ⅰⅰ)配体的作用是建立一个负电荷势场(晶体场),在晶体场的 微扰下,金属的d轨道发生能级分裂。 (ⅰⅰi)金属的电子从低到高填充分裂后的d轨道,使总能量下降,产 生附加成键效应。分裂后总能量的下降称晶体场稳定化能(CFSE)
2. 晶体场理论 4 1)、基本思想 金属配合物的成键类似于离子晶体中正负离子的作用。 (i)金属与配体的作用为静电作用,配体视为点电荷。 (i i)配体的作用是建立一个负电荷势场(晶体场),在晶体场的 微扰下,金属的 d 轨道发生能级分裂。 (i i i)金属的电子从低到高填充分裂后的 d 轨道,使总能量下降,产 生附加成键效应。分裂后总能量的下降称晶体场稳定化能(CFSE) 。 5.3 金属配合物晶体场理论

金属配合物晶体场理论 2.晶体场理论 2)、正八面体场中d轨道分裂的初步处理(0场) (i)中心离子的电子Hamiltonian(只考虑d电子) ia=∑h(m) 采用单电子理论框架(不考虑电子-电子作用项) i=:-子+(←1同=反-r话 h, 为自由离子中d电子的哈密顿算符 ) 为配体的静电场,它有0对称性
2. 晶体场理论 5 2)、正八面体场中d轨道分裂的初步处理(Oh场) (i)中心离子的电子Hamiltonian(只考虑d电子) 采用单电子理论框架(不考虑电子-电子作用项) 为配体的静电场,它有Oh对称性。 ( ) ˆ ˆ H h n n d ( ) ˆ ( 1) 21 ( ) ˆ 2 n ne n V r rZ h n r ( ) ˆ ˆ 0 n h V rr 为自由离子中 d 电子的 哈密顿算符 0ˆh ( ) ˆ n V rr 金属配合物晶体场理论

金属配合物晶体场理论 2.晶体场理论 设配体带电为-q,。 配体-金属原子距离为a L5 。在点电荷模型下,利用经典静电学结果,可 得: a V=-6 g+0 a 前者为各向同性部分,后者为各向异性部分。 oh在0,的对称操作作用下不变。 球坐标系下: (sincos)+(insin)(c >6
2. 晶体场理论 6 在Oh的对称操作作用下不变 。 设配体带电为 -q ,配体-金属原子距离为 a 。在点电荷模型下,利用经典静电学结果,可 得: 前者为各向同性部分,后者为各向异性部分。 ) 53 ( 4 6 35 ˆ 4 4 4 4 5 x y z r aq aq V Voh a q V ˆ 6 ˆ ] 53 [(sin cos ) (sin sin ) (cos ) 5 4 4 4 3 4 4 4 4 4 x y z r r VOh ˆ 球坐标系下: L2 L1 L3 L4 L5 L6 x y z 金属配合物晶体场理论

金属配合物晶体场理论 2.晶体场理论 单电子薛定谔方程: (h。+h)y,=£, 方=-f=69+o, a 用微扰法近似求解单电子薛定谔方程。 电子总波函数: 平a=41…n〉 电子总能量: Eg=∑s 由此可了解配合物的各种性质(稳定性,光谱,磁性..) 7
2. 晶体场理论 7 单电子薛定谔方程: h h i i i ') ˆ ˆ ( 0 d 1 n i d i 用微扰法近似求解单电子薛定谔方程。 由此可了解配合物的各种性质(稳定性,光谱,磁性…) 电子总波函数: 电子总能量: Voh a q h V ˆ 6 ˆ ' ˆ 金属配合物晶体场理论

金属配合物晶体场理论 2.晶体场理论 (iⅱ)d轨道分裂模式:由晶体场的对称性决定。 对于正八面体场,5个d轨道按0群的不可约表示分类 (查特征标表或相关表) 中心力场 0♪的不可约表示 12g d」 原来简并的d轨道分裂为两组:eg和t2g >8
2. 晶体场理论 8 (ii)d轨道分裂模式:由晶体场的对称性决定。 中心力场 Oh的不可约表示 对于正八面体场,5个d轨道 按Oh群的不可约表示分类 (查特征标表或相关表) 原来简并的 d 轨道分裂为两组:eg 和 t2g。 g z x y g zx yz xy e d d t d d d 2 2 2 2 金属配合物晶体场理论
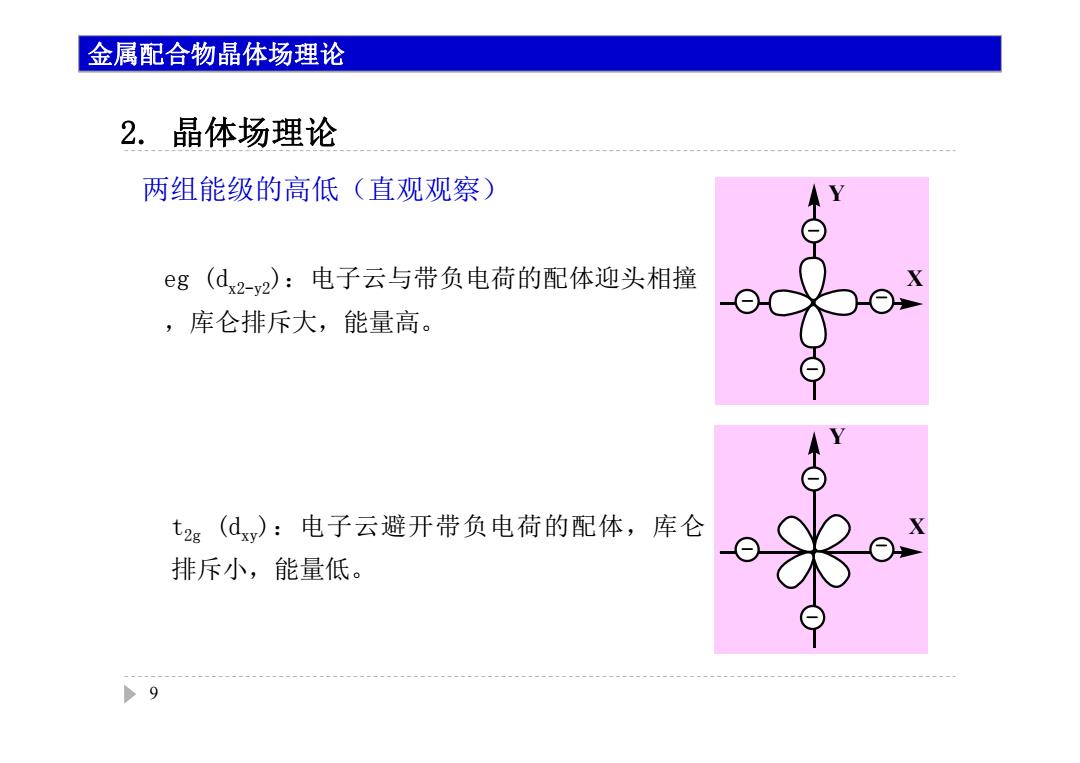
金属配合物晶体场理论 2.晶体场理论 两组能级的高低(直观观察) eg(d2-y2):电子云与带负电荷的配体迎头相撞 ,库仑排斥大,能量高。 t2g(dxy):电子云避开带负电荷的配体,库仑 排斥小,能量低。 >9
2. 晶体场理论 9 两组能级的高低(直观观察) eg (dx2-y2):电子云与带负电荷的配体迎头相撞 ,库仑排斥大,能量高。 Y X Y t2g (dxy):电子云避开带负电荷的配体,库仑 X 排斥小,能量低。 金属配合物晶体场理论

金属配合物晶体场理论 2.晶体场理论 两组能级的高低(直观观察) 04 dx2-y2 dz2 △:分裂能 dxy dyz dxz >10
2. 晶体场理论 10 两组能级的高低(直观观察) 金属配合物晶体场理论 g e 2g t : 分裂能