
6.11无监督学习 聚类算法 K近邻 主成分分析
6.11 无监督学习 聚类算法 K近邻 主成分分析

引言 口无监督算法处理的是那些没有标记的数据: ·缺乏足够的先验知识,因此难以人工标注类别: ·进行人工类别标注的成本太高。 口希望计算机能代我们(部分)完成这些工作,或至少提供一些帮助。 常见的应用背景包括: ·从庞大的样本集合中选出一些具有代表性的加以标注用于分类器的训练: ·先将所有样本自动分为不同的类别,再由人类对这些类别进行标注; ·在无类别信息情况下,寻找好的特征。 口常用算法 ·主成分分析方法PCA等,等距映射方法、局部线性嵌入方法、拉普拉斯 特征映射方法、黑塞局部线性嵌入方法和局部切空间排列方法等
引言 无监督算法处理的是那些没有标记的数据: • 缺乏足够的先验知识,因此难以人工标注类别; • 进行人工类别标注的成本太高。 希望计算机能代我们(部分)完成这些工作,或至少提供一些帮助。 常见的应用背景包括: • 从庞大的样本集合中选出一些具有代表性的加以标注用于分类器的训练; • 先将所有样本自动分为不同的类别,再由人类对这些类别进行标注; • 在无类别信息情况下,寻找好的特征。 常用算法 • 主成分分析方法PCA等,等距映射方法、局部线性嵌入方法、拉普拉斯 特征映射方法、黑塞局部线性嵌入方法和局部切空间排列方法等
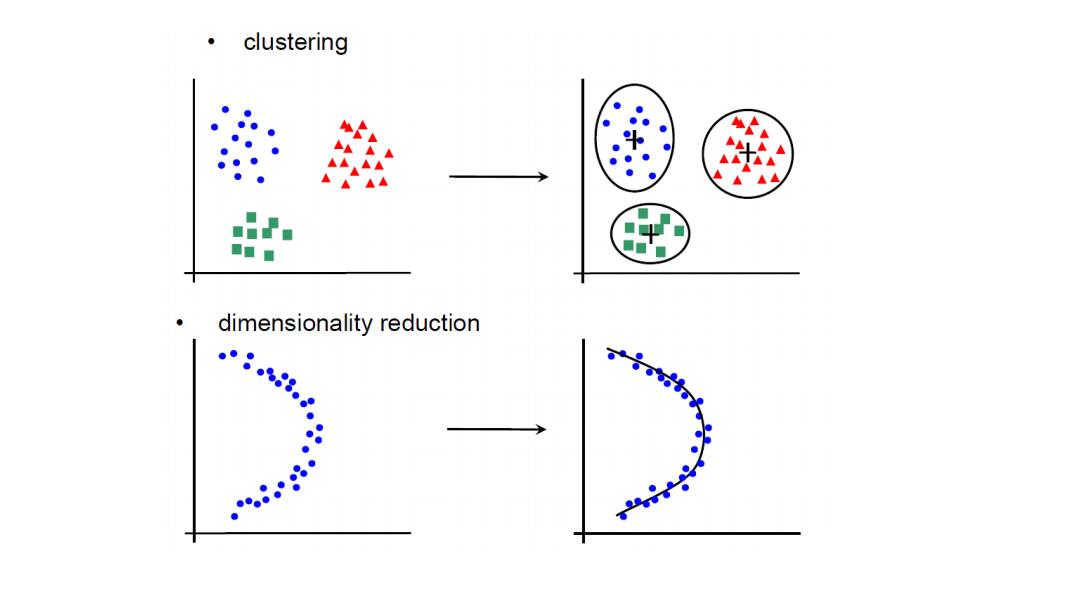
clustering ■■■ dimensionality reduction ● ●● ● ●● ● ●●●●
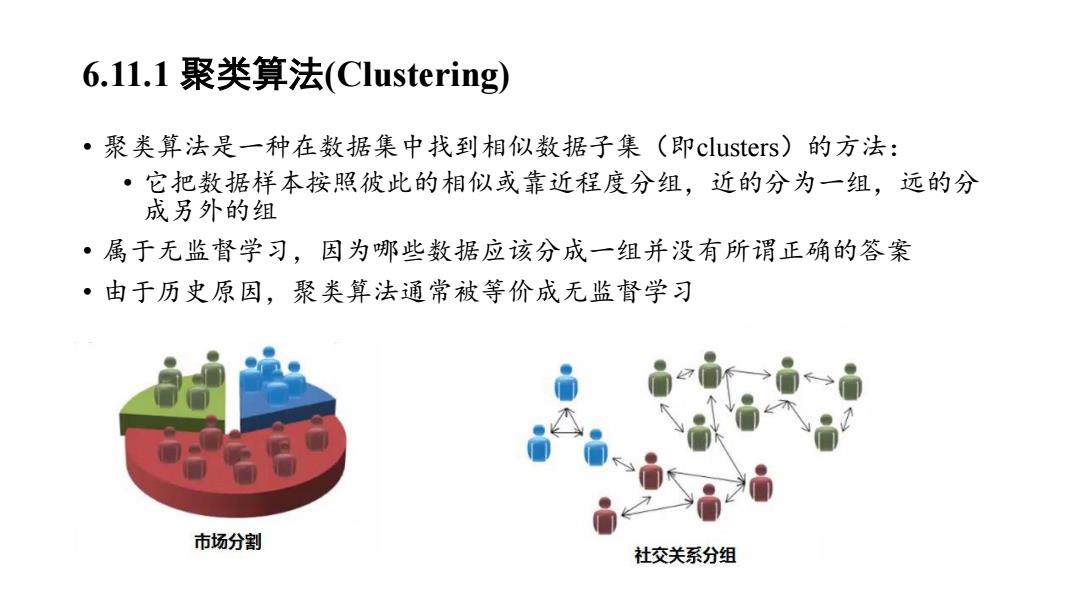
6.11.1聚类算法(Clustering) ·聚类算法是一种在数据集中找到相似数据子集(即clusters)的方法: ·它把数据样本按照彼此的相似或靠近程度分组,近的分为一组,远的分 成另外的组 ·属于无监督学习,因为哪些数据应该分成一组并没有所谓正确的答案 ·由于历史原因,聚类算法通常被等价成无监督学习 市场分割 社交关系分组
6.11.1 聚类算法(Clustering) • 聚类算法是一种在数据集中找到相似数据子集(即clusters)的方法: • 它把数据样本按照彼此的相似或靠近程度分组,近的分为一组,远的分 成另外的组 • 属于无监督学习,因为哪些数据应该分成一组并没有所谓正确的答案 • 由于历史原因,聚类算法通常被等价成无监督学习

聚类算法的分类 ·划分方法 ·划分聚类算法通过优化误差函数把数据集分割为K个部分,它需要K作为 输人参数。 ·典型的分割聚类算法有K-means算法,K-medoids.算法、CLARANS算法。 ·层次方法 ·层次聚类由不同层次的分割聚类组成,层次之间的分割具有嵌套的关系。 ·不需要输入参数,这是它优于分割聚类算法的一个明显的优点,其缺点 是终止条件必须具体指定。 ·典型的分层聚类算法有BIRCH算法、DBSCAN算法和CURE算法等。 ·基于密度的聚类方法 ·基于网格的聚类方法 ·具有模型的聚类方法
聚类算法的分类 • 划分方法 • 划分聚类算法通过优化误差函数把数据集分割为K个部分,它需要K作为 输人参数。 • 典型的分割聚类算法有K-means算法, K-medoids算法、CLARANS算法。 • 层次方法 • 层次聚类由不同层次的分割聚类组成,层次之间的分割具有嵌套的关系。 • 不需要输入参数,这是它优于分割聚类 算法的一个明显的优点,其缺点 是终止条件必须具体指定。 • 典型的分层聚类算法有BIRCH算法、DBSCAN算法和CURE算法等。 • 基于密度的聚类方法 • 基于网格的聚类方法 • 具有模型的聚类方法 • …
K均值(K-means)算法 ·K均值(K-means)算法是现在广泛使用的聚类方法。 3 0 3 5 2 3
K均值(K-means)算法 • K均值(K-means)算法是现在广泛使用的聚类方法
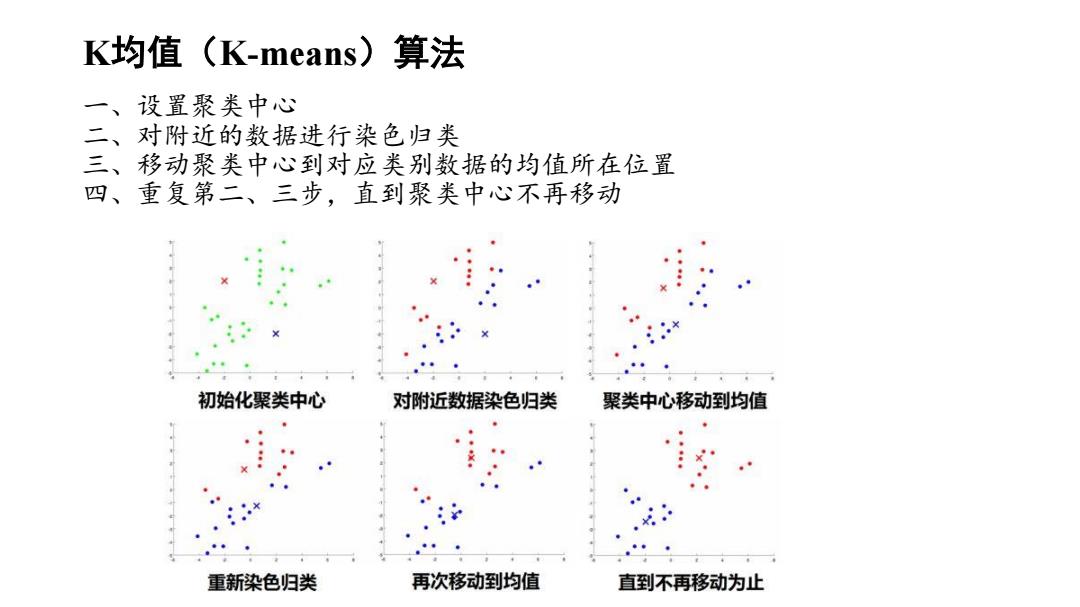
K均值(K-means)算法 一、设置聚类中心 二、对附近的数据进行染色归类 三、移动聚类中心到对应类别数据的均值所在位置 四、重复第二、三步,直到聚类中心不再移动 初始化聚类中心 对附近数据染色归类 聚类中心移动到均值 重新染色归类 再次移动到均值 直到不再移动为止
K均值(K-means)算法 一、设置聚类中心 二、对附近的数据进行染色归类 三、移动聚类中心到对应类别数据的均值所在位置 四、重复第二、三步,直到聚类中心不再移动

K均值(K-means)算法 一、假如对于训练样本集{X,x2,…,七n},有K个聚类{4,h,…,},计算 每个样本和聚类中心的距离: lx-4l 找出离x,最近的k,计C,=j。 二、对于聚类中心,找出其对应的所有x,将它们的中心坐标求出,成为新的 4 三、误差函数:使得各个数据点距离聚类中心的距离 总和最小,也就是图中所有红线和蓝线加起来的总长 度最小。 xi-uc
K均值(K-means)算法 一、假如对于训练样本集 { x1 , x2 , … , xn } ,有 K 个聚类{ 1 , 2 , … , K },计算 每个样本和聚类中心的距离: || xi - j || 找出离xi最近的K,计Ci = j。 二、对于聚类中心j,找出其对应的所有xi,将它们的中心坐标求出,成为新的 j: 三、误差函数: 使得各个数据点距离聚类中心的距离 总和最小,也就是图中所有红线和蓝线加起来的总长 度最小。 𝐿 = 1 𝑛 𝑖=1 𝑛 𝒙𝑖 − 𝝁𝐶𝑖 𝝁𝑗 = 1 𝑁𝑗 𝑖∈𝜇𝑗 𝑁𝑗 xi
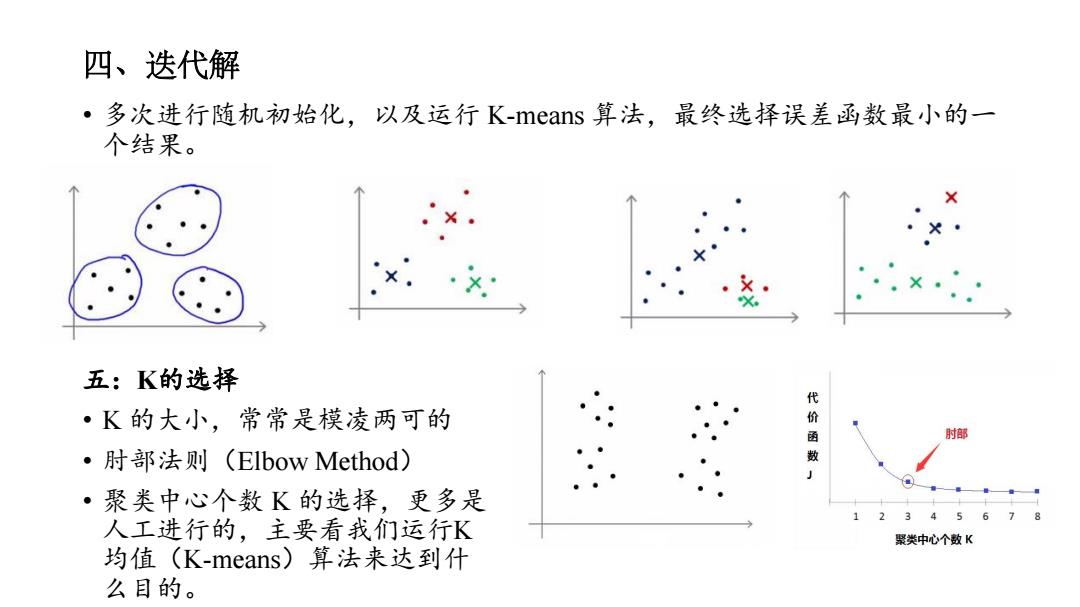
四、迭代解 ·多次进行随机初始化,以及运行K-means算法,最终选择误差函数最小的一 个结果。 五:K的选择 代 ·K的大小,常常是模凌两可的 部 ·肘部法则(Elbow Method) 数 ·聚类中心个数K的选择,更多是 567 人工进行的,主要看我们运行K 聚类中心个数K 均值(K-means)算法来达到什 么目的
四、迭代解 • 多次进行随机初始化,以及运行 K-means 算法,最终选择误差函数最小的一 个结果。 五:K的选择 • K 的大小,常常是模凌两可的 • 肘部法则(Elbow Method) • 聚类中心个数 K 的选择,更多是 人工进行的,主要看我们运行K 均值(K-means)算法来达到什 么目的

6.11.2主成分分析(Principle Component Analysis,PCA) ·通过正交变换将一组可能存在相关性的变量转换为一组线性不相 关的变量,转换后的这组变量叫主成分。 ·主成分分析首先是由K.皮尔森(KarI Pearson)对非随机变量引 入的,尔后H.霍特林将此方法推广到随机向量的情形。 ·主成分分析就是试图在力保数据信息丢失最少的原则下,对这种 多变量的数据表进行最佳综合简化,也就是说,对高维变量空间 进行降维处理。 ·是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除 等领域都有广泛的应用
6.11.2 主成分分析(Principle Component Analysis, PCA) • 通过正交变换将一组可能存在相关性的变量转换为一组线性不相 关的变量,转换后的这组变量叫主成分。 • 主成分分析首先是由K.皮尔森(Karl Pearson)对非随机变量引 入的,尔后H.霍特林将此方法推广到随机向量的情形。 • 主成分分析就是试图在力保数据信息丢失最少的原则下,对这种 多变量的数据表进行最佳综合简化,也就是说,对高维变量空间 进行降维处理。 • 是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除 等领域都有广泛的应用