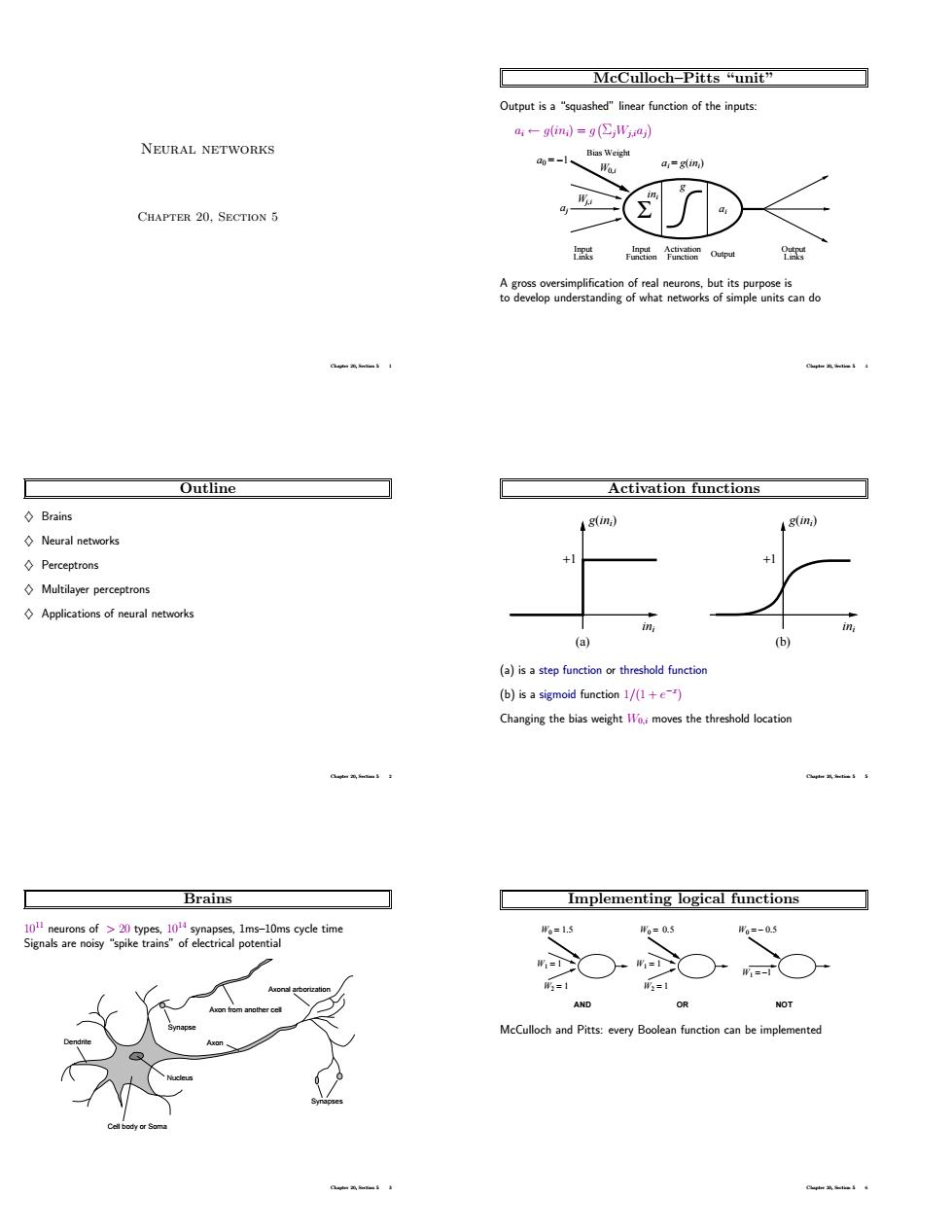
McCulloch-Pitts "unit" Output isaqshedlinear function of the inputs: ←9=g， NEURAL NETWORKS ai-gi) CHAPTER 20,SECTION 5 了-< 器。mo空 ACesoeIenpiaienoredneurcbgt5plpoeno Outline Activation functions ◇Brains g(mna ◇Neural net ◇Perceptrons Multilayer perceptrons (a) (a)is a step function or threshold functio (b)is a sigmoid function 1/(1 Brains Implementing logical functions =03 -05 ○○○ AND OR NOT Neural networks Chapter 20, Section 5 Chapter 20, Section 5 1 Outline ♦ Brains ♦ Neural networks ♦ Perceptrons ♦ Multilayer perceptrons ♦ Applications of neural networks Chapter 20, Section 5 2 Brains 1011 neurons of > 20 types, 1014 synapses, 1ms–10ms cycle time Signals are noisy “spike trains” of electrical potential Axon Cell body or Soma Nucleus Dendrite Synapses Axonal arborization Axon from another cell Synapse Chapter 20, Section 5 3 McCulloch–Pitts “unit” Output is a “squashed” linear function of the inputs: ai ← g(ini) = g  ΣjWj,iaj  Output Σ Input Links Activation Function Input Function Output Links a0 = −1 ai = g(ini ) ai g W ini j,i W0,i Bias Weight aj A gross oversimplification of real neurons, but its purpose is to develop understanding of what networks of simple units can do Chapter 20, Section 5 4 Activation functions (a) (b) +1 +1 ini ini g(ini g(in ) i ) (a) is a step function or threshold function (b) is a sigmoid function 1/(1 + e −x ) Changing the bias weight W0,i moves the threshold location Chapter 20, Section 5 5 Implementing logical functions AND W0 = 1.5 W1 = 1 W2 = 1 OR W2 = 1 W1 = 1 W0 = 0.5 NOT W1 = –1 W0 = – 0.5 McCulloch and Pitts: every Boolean function can be implemented Chapter 20, Section 5 6