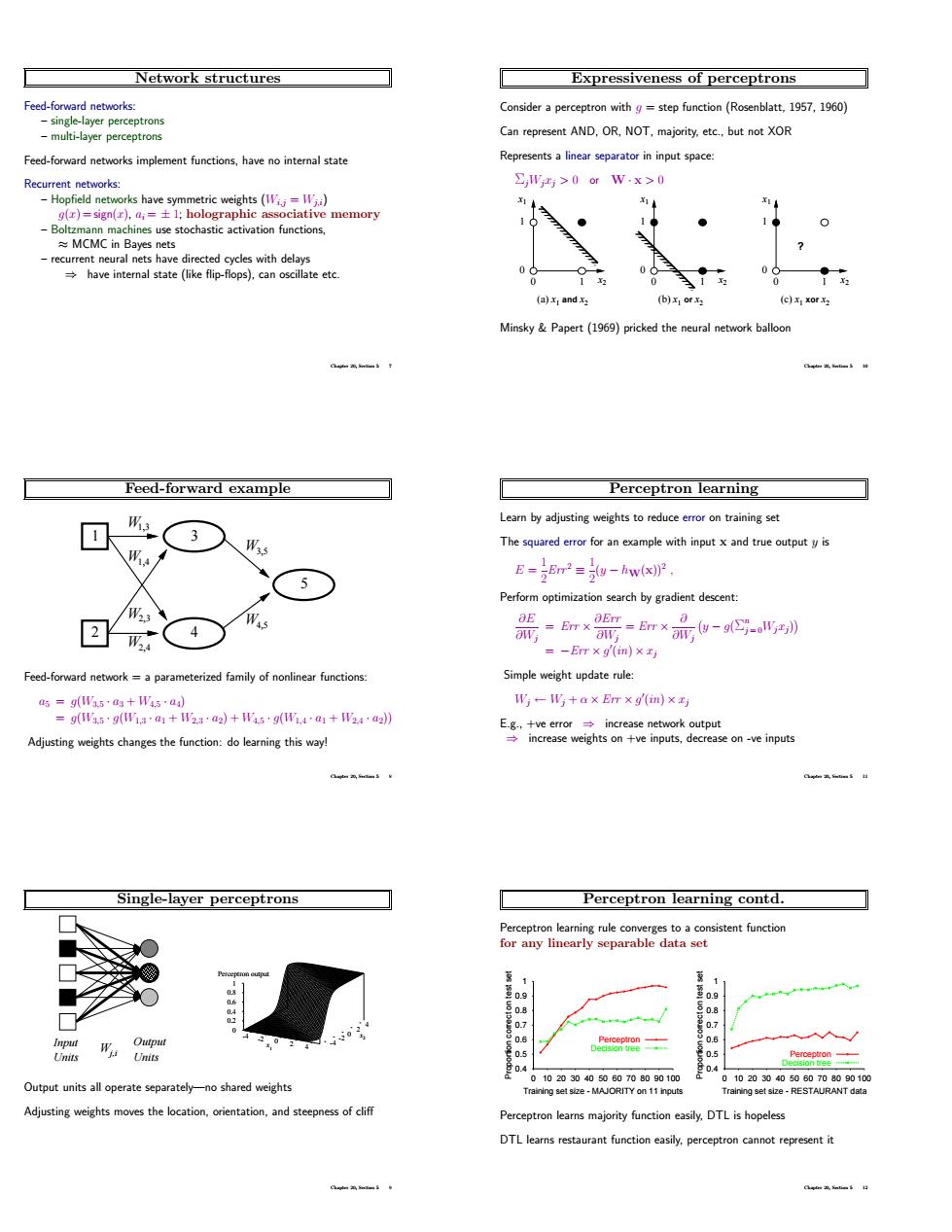
Network structures Expressiveness of perceptrons eed-forward networks Consider a perceptron with g step function (Rosenblatt.1957.1960) Can represent AND,R,NOT,majority ete but eed-fowardetrk implement Represents a linear separator in input space: 4>0wx>0 eocdhascaiatonfacl (a)x1 and xz (c)x xorx MinskyPapert (1)pricked the balloo Feed-forward example Perceptron learning 回 3● W The squared error for an example with input x and true output y is E-Em-hw(x) 5 Perform optimization search by gradient descent: 回 (4 :m×-.= Feed-forward network a parameterized family of nonlinear functions update rule 形一形+ax Ex(m)×写 Adjusting weights changes the function:do eaing this way! Single-layer perceptrons Perceptron learning contd. tent functio Outout units all pperate separately-no shared weishts Adjusting weights m the location and s Perceptron learns majority function easily.DTL is hopeles DTL learns restaurant function easily.perceptro nnot teoresent itNetwork structures Feed-forward networks: – single-layer perceptrons – multi-layer perceptrons Feed-forward networks implement functions, have no internal state Recurrent networks: – Hopfield networks have symmetric weights (Wi,j = Wj,i) g(x) = sign(x), ai = ± 1; holographic associative memory – Boltzmann machines use stochastic activation functions, ≈ MCMC in Bayes nets – recurrent neural nets have directed cycles with delays ⇒ have internal state (like flip-flops), can oscillate etc. Chapter 20, Section 5 7 Feed-forward example W1,3 W1,4 W2,3 W2,4 W3,5 W4,5 1 2 3 4 5 Feed-forward network = a parameterized family of nonlinear functions: a5 = g(W3,5 · a3 + W4,5 · a4) = g(W3,5 · g(W1,3 · a1 + W2,3 · a2) + W4,5 · g(W1,4 · a1 + W2,4 · a2)) Adjusting weights changes the function: do learning this way! Chapter 20, Section 5 8 Single-layer perceptrons Input Units Units Output Wj,i -4 -2 0 2 x1 4 -4 -2 0 2 4 x2 0 0.2 0.4 0.6 0.8 1 Perceptron output Output units all operate separately—no shared weights Adjusting weights moves the location, orientation, and steepness of cliff Chapter 20, Section 5 9 Expressiveness of perceptrons Consider a perceptron with g = step function (Rosenblatt, 1957, 1960) Can represent AND, OR, NOT, majority, etc., but not XOR Represents a linear separator in input space: ΣjWjxj > 0 or W · x > 0 (a) x1 and x2 1 0 0 1 x1 x2 (b) x1 or x2 0 1 1 0 x1 x2 (c) x1 xor x2 ? 0 1 1 0 x1 x2 Minsky & Papert (1969) pricked the neural network balloon Chapter 20, Section 5 10 Perceptron learning Learn by adjusting weights to reduce error on training set The squared error for an example with input x and true output y is E = 1 2 Err 2 ≡ 1 2 (y − hW(x))2 , Perform optimization search by gradient descent: ∂E ∂Wj = Err × ∂Err ∂Wj = Err × ∂ ∂Wj  y − g(Σ n j = 0Wjxj)  = −Err × g 0 (in) × xj Simple weight update rule: Wj ← Wj + α × Err × g 0 (in) × xj E.g., +ve error ⇒ increase network output ⇒ increase weights on +ve inputs, decrease on -ve inputs Chapter 20, Section 5 11 Perceptron learning contd. Perceptron learning rule converges to a consistent function for any linearly separable data set 0.4 0.5 0.6 0.7 0.8 0.9 1 Proportion correct on test set 0 10 20 30 40 50 60 70 80 90 100 Training set size - MAJORITY on 11 inputs Perceptron Decision tree 0.4 0.5 0.6 0.7 0.8 0.9 1 Proportion correct on test set 0 10 20 30 40 50 60 70 80 90 100 Training set size - RESTAURANT data Perceptron Decision tree Perceptron learns majority function easily, DTL is hopeless DTL learns restaurant function easily, perceptron cannot represent it Chapter 20, Section 5 12