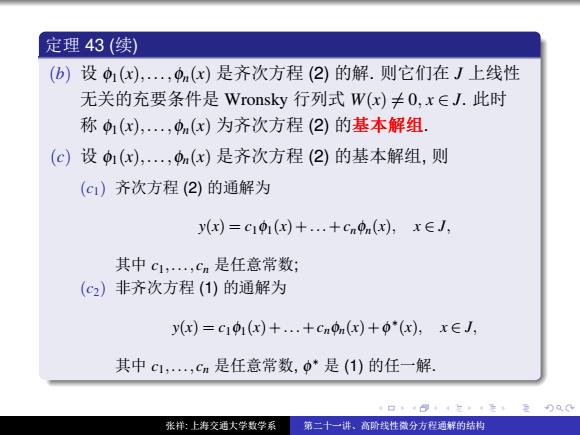
定理43（续） (b)设1(x),,(x)是齐次方程(2)的解.则它们在J上线性 无关的充要条件是Wronsky行列式W(x)≠0，x∈J.此时 称1(x),,(x)为齐次方程(2)的基本解组 (c)设1(x),,(x)是齐次方程(2)的基本解组，则 (c1)齐次方程(2)的通解为 y(x)=c101(x)+...+cnon(x),xEJ, 其中c1,,cn是任意常数： (c2)非齐次方程(1)的通解为 y(x)=c101(x)+...+cnon(x)+o*(x),xEJ, 其中c1,,cn是任意常数，o*是(1)的任一解. 张样：上海交通大学数学系 第二十一讲、高阶线性微分方程通解的结构 ½n 43 (Y) (b)  φ1(x),...,φn(x) ¥‡gêß (2) ). KßÇ3 J ˛Ç5 Ã'øá^ᥠWronsky 1™ W(x) 6= 0, x ∈ J. dû ° φ1(x),...,φn(x) è‡gêß (2) ƒ)|. (c)  φ1(x),...,φn(x) ¥‡gêß (2) ƒ)|, K (c1) ‡gêß (2) œ)è y(x) = c1φ1(x) +...+cnφn(x), x ∈ J, Ÿ• c1,..., cn ¥?ø~Í; (c2) ö‡gêß (1) œ)è y(x) = c1φ1(x) +...+cnφn(x) +φ ∗ (x), x ∈ J, Ÿ• c1,..., cn ¥?ø~Í, φ ∗ ¥ (1) ?ò). ‹å: ˛°œåÆÍÆX 1õò˘!pÇ5á©êßœ)(