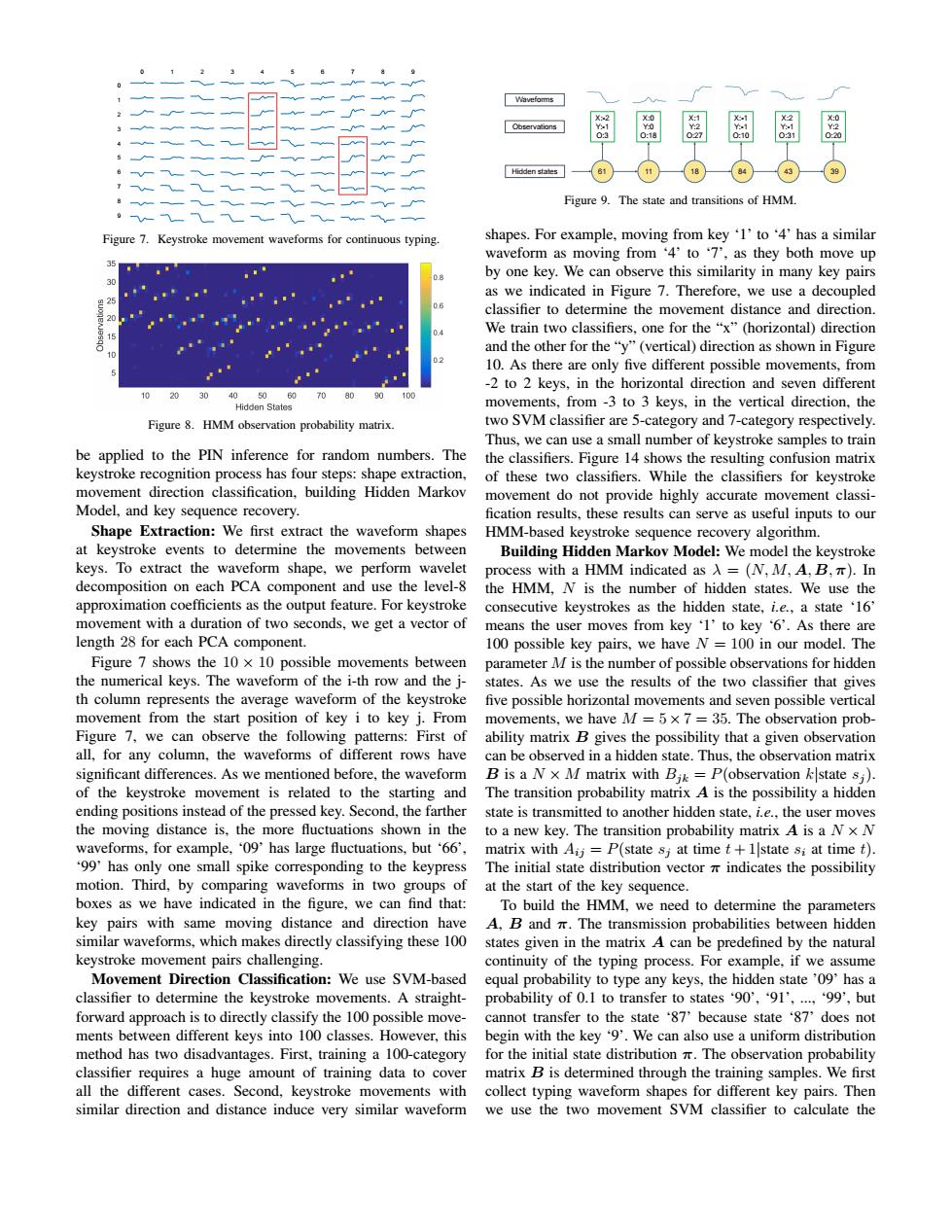
的vefomms 恩恩阁阁恩 Hidden states 61 39 Figure 9.The state and transitions of HMM. Figure 7. Keystroke movement waveforms for continuous typing. shapes.For example,moving from key '1'to '4'has a similar waveform as moving from '4'to '7',as they both move up D.8 by one key.We can observe this similarity in many key pairs as we indicated in Figure 7.Therefore,we use a decoupled classifier to determine the movement distance and direction. We train two classifiers,one for the "x"(horizontal)direction and the other for the"y"(vertical)direction as shown in Figure 10 0.2 10.As there are only five different possible movements,from -2 to 2 keys,in the horizontal direction and seven different 10 20304050607080 0 1D0 Hidden States movements,from -3 to 3 keys,in the vertical direction,the Figure 8.HMM observation probability matrix. two SVM classifier are 5-category and 7-category respectively. Thus,we can use a small number of keystroke samples to train be applied to the PIN inference for random numbers.The the classifiers.Figure 14 shows the resulting confusion matrix keystroke recognition process has four steps:shape extraction, of these two classifiers.While the classifiers for keystroke movement direction classification,building Hidden Markov movement do not provide highly accurate movement classi- Model,and key sequence recovery. fication results,these results can serve as useful inputs to our Shape Extraction:We first extract the waveform shapes HMM-based keystroke sequence recovery algorithm. at keystroke events to determine the movements between Building Hidden Markov Model:We model the keystroke keys.To extract the waveform shape,we perform wavelet process with a HMM indicated as A =(N,M,A,B,)In decomposition on each PCA component and use the level-8 the HMM.N is the number of hidden states.We use the approximation coefficients as the output feature.For keystroke consecutive keystrokes as the hidden state,i.e.,a state '16' movement with a duration of two seconds,we get a vector of means the user moves from key '1'to key '6'.As there are length 28 for each PCA component. 100 possible key pairs,we have N=100 in our model.The Figure 7 shows the 10 x 10 possible movements between parameter M is the number of possible observations for hidden the numerical keys.The waveform of the i-th row and the j- states.As we use the results of the two classifier that gives th column represents the average waveform of the keystroke five possible horizontal movements and seven possible vertical movement from the start position of key i to key j.From movements,we have M=5x 7=35.The observation prob- Figure 7,we can observe the following patterns:First of ability matrix B gives the possibility that a given observation all,for any column,the waveforms of different rows have can be observed in a hidden state.Thus.the observation matrix significant differences.As we mentioned before,the waveform B is a Nx M matrix with Bik=P(observation kstate sj). of the keystroke movement is related to the starting and The transition probability matrix A is the possibility a hidden ending positions instead of the pressed key.Second,the farther state is transmitted to another hidden state,i.e..the user moves the moving distance is,the more fluctuations shown in the to a new key.The transition probability matrix A is a Nx N waveforms.for example.'09'has large fluctuations.but '66'. matrix with Aij =P(state sj at time t+1state si at time t). 99'has only one small spike corresponding to the keypress The initial state distribution vector indicates the possibility motion.Third,by comparing waveforms in two groups of at the start of the key sequence. boxes as we have indicated in the figure,we can find that: To build the HMM,we need to determine the parameters key pairs with same moving distance and direction have A,B and The transmission probabilities between hidden similar waveforms,which makes directly classifying these 100 states given in the matrix A can be predefined by the natural keystroke movement pairs challenging. continuity of the typing process.For example,if we assume Movement Direction Classification:We use SVM-based equal probability to type any keys,the hidden state'09'has a classifier to determine the keystroke movements.A straight- probability of 0.1 to transfer to states '90',91',...,'99',but forward approach is to directly classify the 100 possible move- cannot transfer to the state '87'because state '87'does not ments between different keys into 100 classes.However,this begin with the key 9'.We can also use a uniform distribution method has two disadvantages.First,training a 100-category for the initial state distribution mr.The observation probability classifier requires a huge amount of training data to cover matrix B is determined through the training samples.We first all the different cases.Second,keystroke movements with collect typing waveform shapes for different key pairs.Then similar direction and distance induce very similar waveform we use the two movement SVM classifier to calculate the           Figure 7. Keystroke movement waveforms for continuous typing. Figure 8. HMM observation probability matrix. be applied to the PIN inference for random numbers. The keystroke recognition process has four steps: shape extraction, movement direction classification, building Hidden Markov Model, and key sequence recovery. Shape Extraction: We first extract the waveform shapes at keystroke events to determine the movements between keys. To extract the waveform shape, we perform wavelet decomposition on each PCA component and use the level-8 approximation coefficients as the output feature. For keystroke movement with a duration of two seconds, we get a vector of length 28 for each PCA component. Figure 7 shows the 10 × 10 possible movements between the numerical keys. The waveform of the i-th row and the j￾th column represents the average waveform of the keystroke movement from the start position of key i to key j. From Figure 7, we can observe the following patterns: First of all, for any column, the waveforms of different rows have significant differences. As we mentioned before, the waveform of the keystroke movement is related to the starting and ending positions instead of the pressed key. Second, the farther the moving distance is, the more fluctuations shown in the waveforms, for example, ‘09’ has large fluctuations, but ‘66’, ‘99’ has only one small spike corresponding to the keypress motion. Third, by comparing waveforms in two groups of boxes as we have indicated in the figure, we can find that: key pairs with same moving distance and direction have similar waveforms, which makes directly classifying these 100 keystroke movement pairs challenging. Movement Direction Classification: We use SVM-based classifier to determine the keystroke movements. A straight￾forward approach is to directly classify the 100 possible move￾ments between different keys into 100 classes. However, this method has two disadvantages. First, training a 100-category classifier requires a huge amount of training data to cover all the different cases. Second, keystroke movements with similar direction and distance induce very similar waveform X:-2 Y:-1 O:3 X:0 Y:0 O:18 X:1 Y:2 O:27 X:-1 Y:-1 O:10 X:2 Y:-1 O:31 X:0 Y:2 O:20 61 11 18 84 43 39 Waveforms Observations Hidden states Figure 9. The state and transitions of HMM. shapes. For example, moving from key ‘1’ to ‘4’ has a similar waveform as moving from ‘4’ to ‘7’, as they both move up by one key. We can observe this similarity in many key pairs as we indicated in Figure 7. Therefore, we use a decoupled classifier to determine the movement distance and direction. We train two classifiers, one for the “x” (horizontal) direction and the other for the “y” (vertical) direction as shown in Figure 10. As there are only five different possible movements, from -2 to 2 keys, in the horizontal direction and seven different movements, from -3 to 3 keys, in the vertical direction, the two SVM classifier are 5-category and 7-category respectively. Thus, we can use a small number of keystroke samples to train the classifiers. Figure 14 shows the resulting confusion matrix of these two classifiers. While the classifiers for keystroke movement do not provide highly accurate movement classi- fication results, these results can serve as useful inputs to our HMM-based keystroke sequence recovery algorithm. Building Hidden Markov Model: We model the keystroke process with a HMM indicated as λ = (N, M, A, B,π). In the HMM, N is the number of hidden states. We use the consecutive keystrokes as the hidden state, i.e., a state ‘16’ means the user moves from key ‘1’ to key ‘6’. As there are 100 possible key pairs, we have N = 100 in our model. The parameter M is the number of possible observations for hidden states. As we use the results of the two classifier that gives five possible horizontal movements and seven possible vertical movements, we have M = 5 × 7 = 35. The observation prob￾ability matrix B gives the possibility that a given observation can be observed in a hidden state. Thus, the observation matrix B is a N × M matrix with Bjk = P(observation k|state sj ). The transition probability matrix A is the possibility a hidden state is transmitted to another hidden state, i.e., the user moves to a new key. The transition probability matrix A is a N × N matrix with Aij = P(state sj at time t + 1|state si at time t). The initial state distribution vector π indicates the possibility at the start of the key sequence. To build the HMM, we need to determine the parameters A, B and π. The transmission probabilities between hidden states given in the matrix A can be predefined by the natural continuity of the typing process. For example, if we assume equal probability to type any keys, the hidden state ’09’ has a probability of 0.1 to transfer to states ‘90’, ‘91’, ..., ‘99’, but cannot transfer to the state ‘87’ because state ‘87’ does not begin with the key ‘9’. We can also use a uniform distribution for the initial state distribution π. The observation probability matrix B is determined through the training samples. We first collect typing waveform shapes for different key pairs. Then we use the two movement SVM classifier to calculate the