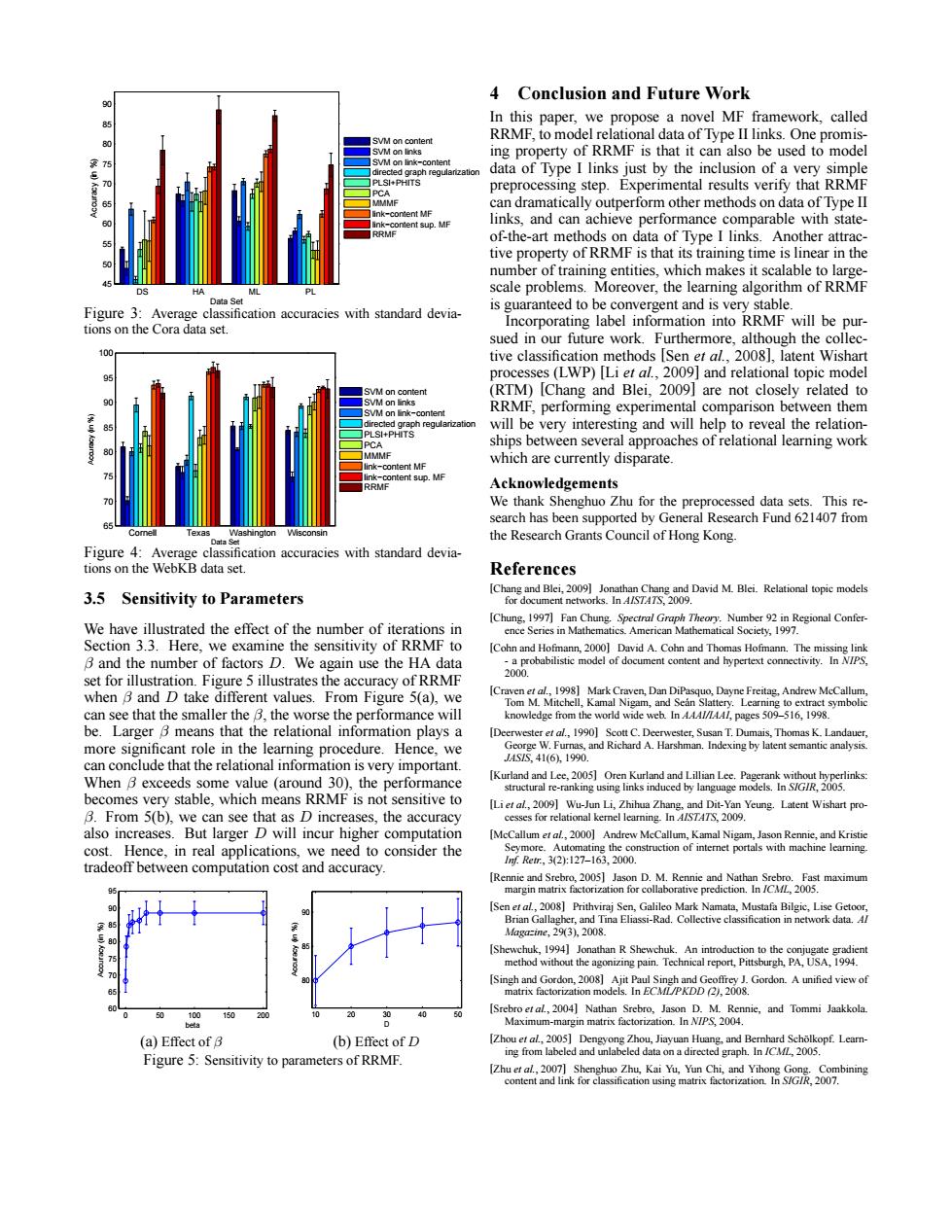
4 Conclusion and Future Work In this paper,we propose a novel MF framework,called SVM oo content RRMF,to model relational data of Type II links.One promis- k ing property of RRMF is that it can also be used to model data of Type I links just by the inclusion of a very simple preprocessing step.Experimental results verify that RRMF can dramatically outperform other methods on data of Type II mtent sup. links,and can achieve performance comparable with state- of-the-art methods on data of Type I links.Another attrac- tive property of RRMF is that its training time is linear in the number of training entities,which makes it scalable to large- DS HA scale problems.Moreover,the learning algorithm of RRMF Data Set Figure 3:Average classification accuracies with standard devia- is guaranteed to be convergent and is very stable. tions on the Cora data set. Incorporating label information into RRMF will be pur- sued in our future work.Furthermore,although the collec- 100 tive classification methods [Sen et al.,2008],latent Wishart processes(LWP)[Li et al.,2009]and relational topic model SVM on content (RTM)[Chang and Blei,2009]are not closely related to RRMF,performing experimental comparison between them will be very interesting and will help to reveal the relation- ships between several approaches of relational learning work MMF which are currently disparate link-content MF link-content sup.MF RRM Acknowledgements We thank Shenghuo Zhu for the preprocessed data sets.This re- search has been supported by General Research Fund 621407 from the Research Grants Council of Hong Kong. Figure 4:Average classification accuracies with standard devia- tions on the WebKB data set. References 3.5 Sensitivity to Parameters [Chang and Blei,2009]Jonathan Chang and David M.Blei.Relational topic models for document networks.In A/S747S,2009. We have illustrated the effect of the number of iterations in [Chung,1997]Fan Chung.Spectral Graph Theory.Number 9 in Regional Confer- ence Series in Mathematics.American Mathematical Society,1997. Section 3.3.Here,we examine the sensitivity of RRMF to [Cohn and Hofmann,2000]David A.Cohn and Thomas Hofmann.The missing link B and the number of factors D.We again use the HA data -a probabilistic model of document content and hypertext connectivity.In NIPS. 2000. set for illustration.Figure 5 illustrates the accuracy of RRMF when B and D take different values.From Figure 5(a),we [Craven etal,199]Mark Craven,Dan DiPasquo,Dayne Freitag,Andrew McCallum. Tom M.Mitchell,Kamal Nigam,and Sean Slattery.Learning to extract symbolic can see that the smaller the B,the worse the performance will knowledge from the world wide web.In A44//144/,pages 509-516,1998. be.Larger B means that the relational information plays a [Deerwester et al.,1990]Scott C.Deerwester,Susan T.Dumais,Thomas K.Landauer, more significant role in the learning procedure.Hence,we George W.Furnas,and Richard A.Harshman.Indexing by latent semantic analysis. can conclude that the relational information is very important. ASS,41(61990 When B exceeds some value (around 30),the performance [Kurland and Lee,2005]Oren Kurland and Lillian Lee.Pagerank without hyperlinks: structural re-ranking using links induced by language models.In S/GIR,2005. becomes very stable,which means RRMF is not sensitive to [Li et al,2009]Wu-Jun Li,Zhihua Zhang,and Dit-Yan Yeung.Latent Wishart pro- B.From 5(b),we can see that as D increases,the accuracy cesses for relational kemnel learning.In A/STATS,2009. also increases.But larger D will incur higher computation [McCallum et al,2000]Andrew McCallum,Kamal Nigam,Jason Rennie,and Kristie cost.Hence,in real applications,we need to consider the Seymore.Automating the construction of internet portals with machine learning. IRer:,32:127-163,2000. tradeoff between computation cost and accuracy [Rennie and Srebro,2005]Jason D.M.Rennie and Nathan Srebro.Fast maximum margin matrix factorization for collaborative prediction.In /CML,2005. [Sen et al,2008]Prithviraj Sen,Galileo Mark Namata,Mustafa Bilgic,Lise Getoor, Brian Gallagher,and Tina Eliassi-Rad.Collective classification in network data.A/ Magazine,29(3),2008. [Shewchuk,1994]Jonathan R Shewchuk.An introduction to the conjugate gradient method without the agonizing pain.Technical report,Pittsburgh,PA.USA,1994. [Singh and Gordon,2008]Ajit Paul Singh and Geoffrey J.Gordon.A unified view of matrix factorization models.In ECML/PKDD (2),2008. 150 [Srebro etal,2004]Nathan Srebro,Jason D.M.Rennie,and Tommi Jaakkola Maximum-margin matrix factorization.In N/PS,2004. (a)Effect of B (b)Effect of D [Zhou etal,2005]Dengyong Zhou,Jiayuan Huang,and Bemhard Scholkopf.Lear- Figure 5:Sensitivity to parameters of RRMF. ing from labeled and unlabeled data on a directed graph.In /CML,2005. [Zhu et al,2007]Shenghuo Zhu,Kai Yu,Yun Chi,and Yihong Gong.Combining content and link for classification using matrix factorization.In S/G/R,2007.DS HA ML PL 45 50 55 60 65 70 75 80 85 90 Data Set Accuracy (in %) SVM on content SVM on links SVM on link−content directed graph regularization PLSI+PHITS PCA MMMF link−content MF link−content sup. MF RRMF Figure 3: Average classification accuracies with standard devia￾tions on the Cora data set. Cornell Texas Washington Wisconsin 65 70 75 80 85 90 95 100 Data Set Accuracy (in %) SVM on content SVM on links SVM on link−content directed graph regularization PLSI+PHITS PCA MMMF link−content MF link−content sup. MF RRMF Figure 4: Average classification accuracies with standard devia￾tions on the WebKB data set. 3.5 Sensitivity to Parameters We have illustrated the effect of the number of iterations in Section 3.3. Here, we examine the sensitivity of RRMF to β and the number of factors D. We again use the HA data set for illustration. Figure 5 illustrates the accuracy of RRMF when β and D take different values. From Figure 5(a), we can see that the smaller the β, the worse the performance will be. Larger β means that the relational information plays a more significant role in the learning procedure. Hence, we can conclude that the relational information is very important. When β exceeds some value (around 30), the performance becomes very stable, which means RRMF is not sensitive to β. From 5(b), we can see that as D increases, the accuracy also increases. But larger D will incur higher computation cost. Hence, in real applications, we need to consider the tradeoff between computation cost and accuracy. 0 50 100 150 200 60 65 70 75 80 85 90 95 beta Accuracy (in %) 10 20 30 40 50 80 85 90 D Accuracy (in %) (a) Effect of β (b) Effect of D Figure 5: Sensitivity to parameters of RRMF. 4 Conclusion and Future Work In this paper, we propose a novel MF framework, called RRMF, to model relational data of Type II links. One promis￾ing property of RRMF is that it can also be used to model data of Type I links just by the inclusion of a very simple preprocessing step. Experimental results verify that RRMF can dramatically outperform other methods on data of Type II links, and can achieve performance comparable with state￾of-the-art methods on data of Type I links. Another attrac￾tive property of RRMF is that its training time is linear in the number of training entities, which makes it scalable to large￾scale problems. Moreover, the learning algorithm of RRMF is guaranteed to be convergent and is very stable. Incorporating label information into RRMF will be pur￾sued in our future work. Furthermore, although the collec￾tive classification methods [Sen et al., 2008], latent Wishart processes (LWP) [Li et al., 2009] and relational topic model (RTM) [Chang and Blei, 2009] are not closely related to RRMF, performing experimental comparison between them will be very interesting and will help to reveal the relation￾ships between several approaches of relational learning work which are currently disparate. Acknowledgements We thank Shenghuo Zhu for the preprocessed data sets. This re￾search has been supported by General Research Fund 621407 from the Research Grants Council of Hong Kong. References [Chang and Blei, 2009] Jonathan Chang and David M. Blei. Relational topic models for document networks. In AISTATS, 2009. [Chung, 1997] Fan Chung. Spectral Graph Theory. Number 92 in Regional Confer￾ence Series in Mathematics. American Mathematical Society, 1997. [Cohn and Hofmann, 2000] David A. Cohn and Thomas Hofmann. The missing link - a probabilistic model of document content and hypertext connectivity. In NIPS, 2000. [Craven et al., 1998] Mark Craven, Dan DiPasquo, Dayne Freitag, Andrew McCallum, Tom M. Mitchell, Kamal Nigam, and Sean Slattery. Learning to extract symbolic ´ knowledge from the world wide web. In AAAI/IAAI, pages 509–516, 1998. [Deerwester et al., 1990] Scott C. Deerwester, Susan T. Dumais, Thomas K. Landauer, George W. Furnas, and Richard A. Harshman. Indexing by latent semantic analysis. JASIS, 41(6), 1990. [Kurland and Lee, 2005] Oren Kurland and Lillian Lee. Pagerank without hyperlinks: structural re-ranking using links induced by language models. In SIGIR, 2005. [Li et al., 2009] Wu-Jun Li, Zhihua Zhang, and Dit-Yan Yeung. Latent Wishart pro￾cesses for relational kernel learning. In AISTATS, 2009. [McCallum et al., 2000] Andrew McCallum, Kamal Nigam, Jason Rennie, and Kristie Seymore. Automating the construction of internet portals with machine learning. Inf. Retr., 3(2):127–163, 2000. [Rennie and Srebro, 2005] Jason D. M. Rennie and Nathan Srebro. Fast maximum margin matrix factorization for collaborative prediction. In ICML, 2005. [Sen et al., 2008] Prithviraj Sen, Galileo Mark Namata, Mustafa Bilgic, Lise Getoor, Brian Gallagher, and Tina Eliassi-Rad. Collective classification in network data. AI Magazine, 29(3), 2008. [Shewchuk, 1994] Jonathan R Shewchuk. An introduction to the conjugate gradient method without the agonizing pain. Technical report, Pittsburgh, PA, USA, 1994. [Singh and Gordon, 2008] Ajit Paul Singh and Geoffrey J. Gordon. A unified view of matrix factorization models. In ECML/PKDD (2), 2008. [Srebro et al., 2004] Nathan Srebro, Jason D. M. Rennie, and Tommi Jaakkola. Maximum-margin matrix factorization. In NIPS, 2004. [Zhou et al., 2005] Dengyong Zhou, Jiayuan Huang, and Bernhard Scholkopf. Learn- ¨ ing from labeled and unlabeled data on a directed graph. In ICML, 2005. [Zhu et al., 2007] Shenghuo Zhu, Kai Yu, Yun Chi, and Yihong Gong. Combining content and link for classification using matrix factorization. In SIGIR, 2007