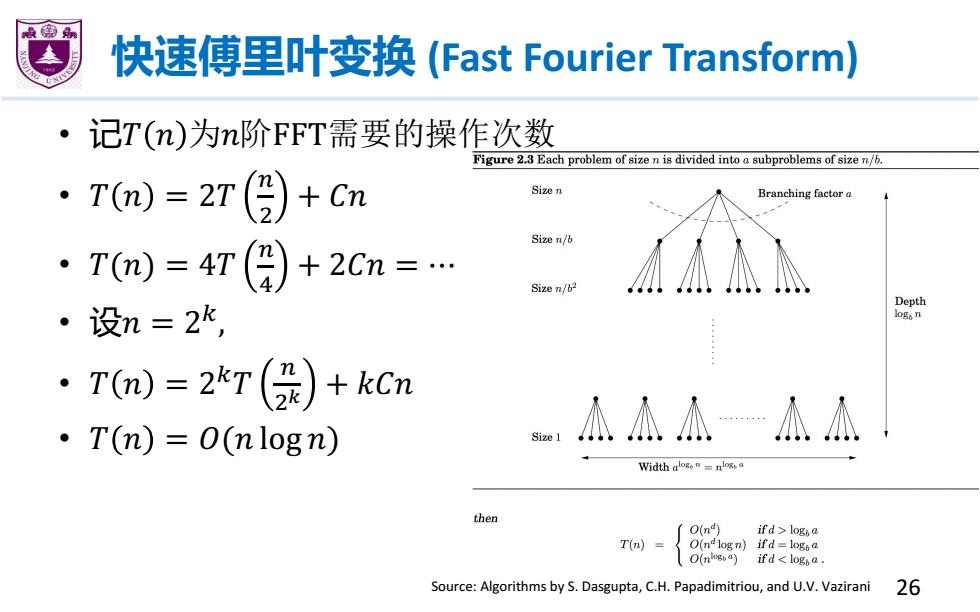
快速傅里叶变换(Fast Fourier Transform) 记T(n)为n阶FFT需要的操作次数 Figure 2.3 Each problem of size n is divided into a subproblems of size n/ ·T(n)=2T(份）+cm Sizen Branching factor a Size n/b ·T(m)=4T(9+2Cn=… Size n/62 Depth ·设n=2k, logo n ·Tm)=2*7() +kCn ·T(n)=O(n log n) Size 1 瓜瓜△瓜瓜」 Width alogs n= then (O(n) if d>loga T() O(ndlogn)if d log6 a O(nga) if d log a Source:Algorithms by S.Dasgupta,C.H.Papadimitriou,and U.V.Vazirani 26快速傅里叶变换 (Fast Fourier Transform) • 记� � 为�阶FFT需要的操作次数 • � � = 2� $ " + �� • �(�) = 4� $ W + 2�� = ⋯ • 设� = 2I , • � � = 2I� $ ") + ��� • � � = �(� log �) Source: Algorithms by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 26