
回顾 通知:第一次作业已经发回到同学们的邮箱:第三次作业今天已经发布 上节课: Chebyshev插值 Chebyshev多项式 最小二乘法离散线性版本:给定矩阵A,向量b,求x使得IAx-b最小 -使用矩阵A的列向量进行线性组合 由法线方程得出x=(ATA)-1ATb 如果正交:x=ATb ·由函数/多项式亦可组成的向量空间 -内积:f,g)w=∫f(x)g(x)w(x)dx -2范数:‖xlw=V(x,x)w 正交通数族仰》-{合引 作业:Gram-Schmidt:过程中,哪些操作对应于“内积”?如何推广到函数空 间? 2
回顾 通知:第一次作业已经发回到同学们的邮箱;第三次作业今天已经发布 上节课: • Chebyshev插值 • Chebyshev多项式 • 最小二乘法-离散线性版本:给定矩阵�,向量�,求�使得 �� − � ! !最小 – 使用矩阵�的列向量进行线性组合 – 由法线方程得出 � = �"� #$�"� – 如果正交:� = �"� • 由函数/多项式亦可组成的向量空间 – 内积: �, � ! ≔ ∫ � � � � �(�)�� – 2范数: � ! = �, � ! – 正交函数族: �",�# = / �", � = � 0, � ≠ � – 作业:Gram-Schmidt过程中,哪些操作对应于“内积”?如何推广到函数空 间? 2

课程计划 最小二乘法的一些建模和应用讨论: ·图像拼接 三角级数近似 傅里叶变换(Fourier Transform) · 复数、单位根 离散傅里叶变换(Discrete Fourier Transform,DFT) 快速傅里叶变换(Fast Fourier Transform,FFT) 。 复杂性分析 。 快速傅里叶变换的逆变换(Inverse FFT) 3
课程计划 最小二乘法的一些建模和应用讨论: • 图像拼接 • 三角级数近似 傅里叶变换 (Fourier Transform) • 复数、单位根 • 离散傅里叶变换 (Discrete Fourier Transform, DFT) • 快速傅里叶变换 (Fast Fourier Transform, FFT) • 复杂性分析 • 快速傅里叶变换的逆变换(Inverse FFT) 3

嫩细 ▲ 最小二乘法建模:图像拼接 照片来源:由本人拍摄于2022-03-18 4
最小二乘法建模:图像拼接 照片来源:由本人拍摄于2022-03-18 4

最小二乘法建模:图像拼接 。 在图片上选取一些参考点(比如同一个建筑,对应的树) 希望找到矩阵A∈R2x2和向量b∈R2 ·使得对于每一个参考点都有 ≈AX +b ·未知量是什么? 思考:值得注意的是这里的量词的顺序 - 如果,对于每一个参考点,都要求找到一个矩阵A∈R2x2和向量 b∈R2最小化误差呢? 5
最小二乘法建模:图像拼接 • 在图片上选取一些参考点(比如同一个建筑,对应的树) • 希望找到矩阵� ∈ ℝ!×!和向量 � ∈ ℝ! • 使得对于每一个参考点都有 • 未知量是什么? • 思考:值得注意的是这里的量词的顺序 – 如果,对于每一个参考点,都要求找到一个矩阵� ∈ ℝ&×&和向量 � ∈ ℝ&最小化误差呢? 5 ≈ �× +�

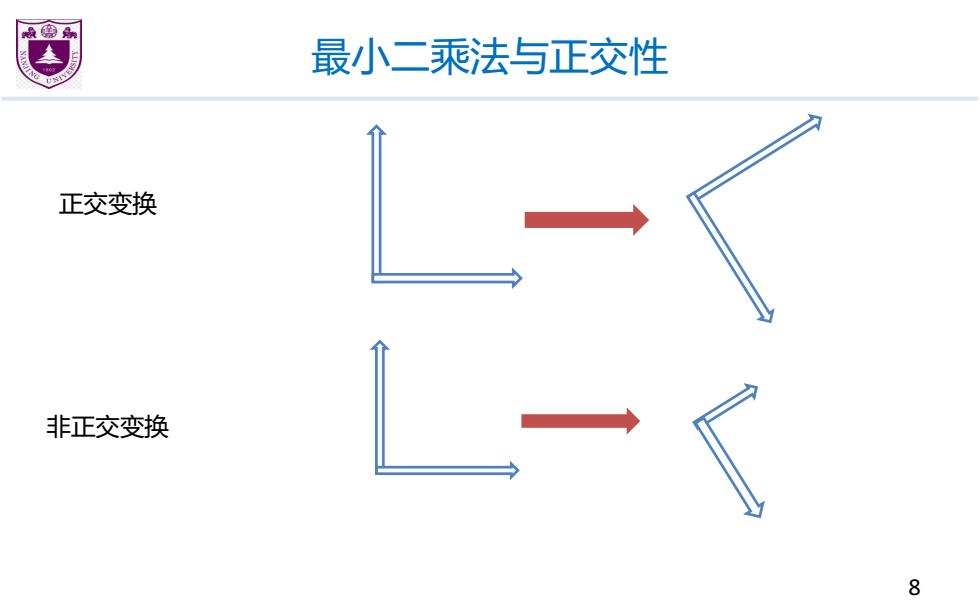
最小二乘法与正交性 给定矩阵A,向量b,求x使得IAx一b最小。 由法线方程ATAX=ATb,得出x=(ATA)-1ATb ·但是,一般数值算法中不会直接求解法线方程 更不会求(ATA)-1 A2 如图所示,不管选A1还是A2,都能给出对b不错的 近似,但是对应的x是非常不一样的 6
最小二乘法与正交性 给定矩阵�,向量�,求�使得 �� − � 5 5最小。 由法线方程 �!�� = �!�,得出 � = �!� "#�!� • 但是,一般数值算法中不会直接求解法线方程 • 更不会求 �!� "# • 如图所示,不管选�#还是 �$,都能给出对�不错的 近似,但是对应的�是非常不一样的 6 � �! �

最小二乘法与正交性 一个更好的做法是通过Gram-Schmidt?求A=QR分解 11 …:0 丫1m ·其中Q为正交阵:QrQ=1 这意味若,9=日 - i=j i≠j ·R为上三角阵 通过QR分解,ATA元=ATb→x=R-1QTb 并不需要计算ATA 实践中,更常用,更数值稳定的是Householder反射子,而不是Gram-Schmidt
最小二乘法与正交性 一个更好的做法是通过Gram-Schmidt求� = ��分解 ⋮ �! ⋮ ⋮ �" ⋮ ⋮ �# ⋮ … ⋮ �$ ⋮ = ⋮ �( ⋮ ⋮ �& ⋮ ⋮ �) ⋮ … ⋮ �* ⋮ �!! … �!$ 0 ⋱ ⋮ 0 0 �$$ • 其中�为正交阵:�%� = � – 这意味着 �+, �, = - 1, � = � 0, � ≠ � • �为上三角阵 通过QR分解, �-�� = �-� ⇒ � = �&!�%� 并不需要计算 �%� 实践中,更常用,更数值稳定的是Householder反射子,而不是Gram-Schmidt 7
嫩细 最小二乘法与正交性 正交变换 非正交变换 8
最小二乘法与正交性 8 正交变换 非正交变换

最小二乘法与正交性 若Q为正交阵:QTQ=I,则lQxl2=lxl2 Isometry:保距映射 思考:除了长度,还可以考虑角度 (Qx,Qy〉=? 9
最小二乘法与正交性 9 若�为正交阵:�!� = �,则 �� " = � " Isometry:保距映射 思考:除了长度,还可以考虑角度 ��,�� =?

正交系统中的最小二乘法:傅里叶级数 给定函数f和一组基函数中,能否找到系数{c}使得 设0= φk(x)=c0s(kx),k=1,2,…,n, n+k (x)=sin(kx),k 1,2,...,n-1 则函数族中o(x),中1(x),…在[-兀,π]上是正交的 证明:cos(kx)和sin(kx)在[-π,π上的积分都为0,再由积化和差公式即可得: 1 sin(y)cos()(sin(-x)+sin+x)) cosy)cos(x)=(cos(y-x)+cosy+x)) 1 sin(y)sin(x)=(cos(y-x)-cos(y+x)) 11
正交系统中的最小二乘法:傅里叶级数 给定函数 �和一组基函数�%,能否找到系数{�"}使得 � � ≈ - " �" �" � 设 �$ = % & , �'(�) = cos(��) , � = 1,2, … , �, �()' � = sin �� , � = 1,2, … , � − 1 则函数族�! � ,�" � , …在[−�, �]上是正交的 证明: cos(��)和 sin �� 在[−�, �]上的积分都为0,再由积化和差公式即可得: sin � cos � = 1 2 (sin � − � + sin(� + �)) cos � cos � = 1 2 (cos � − � + cos(� + �)) sin � sin � = 1 2 (cos � − � − cos(� + �)) 11

正交系统中的最小二乘法:傅里叶级数(选讲) 给定函数f,能否找到系数{a,b}使得 n-1 ao f(x)≈号+an cosnx+ 2 (ak cos kx bk sin kx) k=1 这里也可以使用最小二乘法(sketch): ·记误差函数为 E(x):=f(x)- 00 +an cosnx+】 。 考虑川E(x)匠=(E(x),E(x)》=∫E(x)2dx ·对E(x)陉关于系数{a,b求偏导并设为0, 即得到法线方程 。 由于正交性,可推导得 (f,cos kx) ak= (cos kx,coskx) (f,sin kx) bk= (sin kx,sin kx) 12
正交系统中的最小二乘法:傅里叶级数(选讲) 给定函数 �,能否找到系数{�", �"}使得 � � ≈ �$ 2 + �( cos �� + - '*% (+% �' cos �� + �' sin �� 这里也可以使用最小二乘法(sketch): • 记误差函数为 � � ≔ � � − �& 2 + �' cos �� + > ()$ '#$ �( cos �� + �( sin �� • 考虑 � � & & = � � , �(�) = ∫+, , � � &�� • 对 � � ! !关于系数 {�%, �%}求偏导并设为0,即得到法线方程 • 由于正交性,可推导得 �' = �, cos �� cos �� , cos �� �' = �, sin �� sin �� , sin �� 12