
回顾 上节课: ·随机游走的碰撞时间(Hitting time)和返程时间 (commute time) ·线性规划LP,顶点的不同定义 这节课: ·对偶性 ·零和游戏 2
回顾 上节课: • 随机游走的碰撞时间(Hitting time)和返程时间 (commute time) • 线性规划 LP,顶点的不同定义 这节课: • 对偶性 • 零和游戏 2

LP的顶点 考虑max(c,x),约束在P={Ax≤b这个polytopel内 顶点可以有3种定义: 1. 边角corner)山:如果不存在y≠0使得x+y∈P and x-y∈P,则称点x是一个边角 2. 极值点:如果c使得x是该目标方向c的唯一最优解,则称点x是一个极值点 3. 基本解:如果(A,x)=b:,我们称第i个约束是紧致(tight)的,其中A:是第行 对于给定的x∈P,记A为A中关于x紧致的约束组成的子矩阵 如果A=是满秩的,i.e.rank(A=)=n,那么我们称x是一个基本解 事实上,这3种定义是等价的。 LP的稳定性:对c的扰动,对A的扰动 顶点的个数:一般情况下面可能是指数级别的,(%) 3
LP的顶点 考虑max �, � ,约束在� ≔ {�� ≤ �}这个polytope内 顶点可以有3种定义: 1. 边角(corner): 如果不存在� ≠ 0 使得 � + � ∈ � and � − � ∈ �,则称点�是一个边角 2. 极值点: 如果 ∃� 使得�是该目标方向�的唯一最优解,则称点�是一个极值点. 3. 基本解: 如果 �!, � = �! ,我们称第�个约束是紧致 (tight)的 ,其中 �! 是第�行. 对于给定的� ∈ �, 记 �" 为� 中关于 � 紧致的约束组成的子矩阵. 如果�" 是满秩的, i.e. ���� �" = � ,那么我们称�是一个基本解. 事实上,这3种定义是等价的。 LP的稳定性:对c的扰动,对A的扰动 顶点的个数:一般情况下面可能是指数级别的, # $ 3

LP的顶点 考虑maxc,x),约束在P={Ax≤b}这个polytope内 1边角corner):如果不存在y≠0使得x+y∈P andx-y∈P,则称点x是一个边角 3基本邂:紧致的约束组成的子矩阵A=是满秩的,i.e.rank(A=)=n 1)→3):或者说是3)→1) 假设存在rank(A=)<n,i.e,y≠0,A-y=0 考虑x+Ey,x-ey,注意到 A-(x+cy)=Ax A=(x-Ey)=A-x 取足够小,使得其它的不等式约束不被违反 则有x+ey∈P,x-ey∈P 4
LP的顶点 考虑max �, � ,约束在� ≔ {�� ≤ �}这个polytope内 1.边角(corner): 如果不存在� ≠ 0 使得 � + � ∈ � and � − � ∈ �,则称点�是一个边角 3.基本解: 紧致的约束组成的子矩阵�! 是满秩的, i.e. ���� �! = � 1) ⇒ 3): 或者说是¬3) ⇒ ¬1) 假设存在 ���� �! < �, �. �., ∃� ≠ 0, �!y = 0 考虑� + ��, � − ��,注意到 �! � + �� = �!� �! � − �� = �!� 取�足够小,使得其它的不等式约束不被违反 则有� + �� ∈ �, � − �� ∈ � 4

LP的顶点 考虑max(c,x),约束在P:={Ax≤b}这个polytoper内 1边角(corner山:如果不存在y≠0使得x+y E P andx-y∈P,则称点x是一个 边角 3.基本解:紧致的约束组成的子矩阵A=是满秩的,i.e.rank(A-)=n 3)→1):或者说是1)→3) 假设有y≠0使得x+yEP,x-y∈P A=(x+y)≤b= AF(x-y)≤b= 其中A=x=b= 因此有A=y≤0,A=y≥0进而A=y=0 5
LP的顶点 考虑max �, � ,约束在� ≔ {�� ≤ �}这个polytope内 1.边角(corner): 如果不存在� ≠ 0 使得 � + � ∈ � and � − � ∈ �,则称点�是一个 边角 3.基本解: 紧致的约束组成的子矩阵�; 是满秩的, i.e. ���� �; = � 3) ⇒ 1): 或者说是¬1) ⇒ ¬3) 假设有� ≠ 0使得� + � ∈ �, � − � ∈ � �; � + � ≤ �; �; � − � ≤ �; 其中 �;� = �; 因此有 �;� ≤ 0, �;� ≥ 0进而 �;� = 0 5

LP的顶点 考虑max(c,x),约束在P:={Ax≤b}这个polytope内 顶点可以有3种等价的定义: 边角corner山:如果不存在y≠0使得x+y∈P and x-y∈P,则称点x是一个边角 2 极值点:如果3c使得x是该目标方向c的唯一最优解,则称点x是一个极值点. 基本蟹:如果(4,x)-b:,我们称第i个约束是紧致ght的,其中A:是第行 对于给定的x∈P,记A为A中关于x紧致的约束组成的子矩阵 如果A=是满秩的,i.e.rank(A=)=n,那么我们称x是一个基本解 Simplex算法:从一个顶点开始:找下一个顶点,如果目标函数更优,则选择移到该顶点:重复: 邻居的选择:最多(m-n)n 如果所有邻居都更差,则当前必定是最优的解:对于凸优化问题,局部最优即是全局最优 最坏情况下面,Simplex算法可能需要指数时间。但是实践中表现往往不错,smoothed analysis 多项式算法:Ellipsoid algorithm,interior point methods 6
LP的顶点 考虑max �, � ,约束在� ≔ {�� ≤ �}这个polytope内 顶点可以有3种等价的定义: 1. 边角(corner): 如果不存在� ≠ 0 使得 � + � ∈ � and � − � ∈ �,则称点�是一个边角 2. 极值点: 如果 ∃� 使得�是该目标方向�的唯一最优解,则称点�是一个极值点. 3. 基本解: 如果 �!, � = �! ,我们称第�个约束是紧致 (tight)的 ,其中 �! 是第�行. 对于给定的� ∈ �, 记 �" 为� 中关于 � 紧致的约束组成的子矩阵. 如果�" 是满秩的, i.e. ���� �" = � ,那么我们称�是一个基本解. Simplex算法:从一个顶点开始;找下一个顶点,如果目标函数更优,则选择移到该顶点;重复; 邻居的选择: 最多(m-n)n 如果所有邻居都更差,则当前必定是最优的解:对于凸优化问题,局部最优即是全局最优 最坏情况下面, Simplex算法可能需要指数时间。但是实践中表现往往不错,smoothed analysis 多项式算法; Ellipsoid algorithm, interior point methods 6
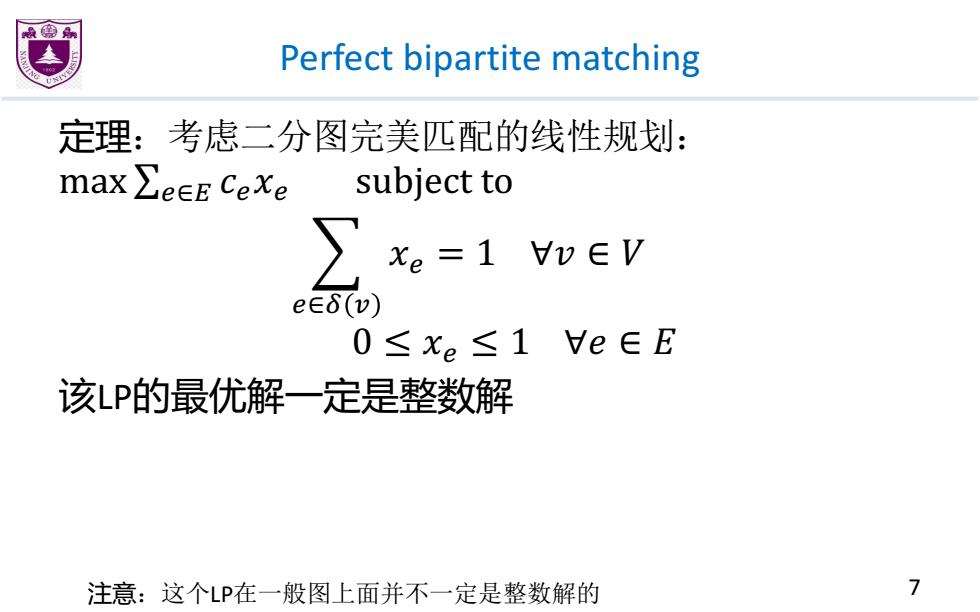
Perfect bipartite matching 定理:考虑二分图完美匹配的线性规划: max∑eEE CeXe subject to xe=1v∈V e∈δ(v) 0≤xe≤1He∈E 该LP的最优解一定是整数解 注意:这个LP在一般图上面并不一定是整数解的 7
Perfect bipartite matching 定理:考虑二分图完美匹配的线性规划: max ∑!∈# �!�! subject to 0 !∈$ % �! = 1 ∀� ∈ � 0 ≤ �! ≤ 1 ∀� ∈ � 该LP的最优解一定是整数解 注意:这个LP在一般图上面并不一定是整数解的 7

Ellipsoid algorithm,separation oracle(选讲) 最小生成树的一种LP写法 ·max∑eEE CeXe ·∑e∈Esxe≤lSI-1, ∑eeE(V)Xe=IV川-1 。0≤xe≤1 虽然是指数大小的LP,但是Ellipsoid algorithm只需要有 separation oracle,也能多项式时间解出来 8
Ellipsoid algorithm, separation oracle (选讲) 最小生成树的一种LP写法 • max ∑!∈# �!�! • ∑!∈#(%) �! ≤ � − 1, ∀� ⊂ � • ∑!∈#(') �! = � − 1 • 0 ≤ �! ≤ 1 虽然是指数大小的LP,但是Ellipsoid algorithm只需要有 separation oracle,也能多项式时间解出来 8

Duality::给目标函数证明上界 max 5x1+4x2 2x1+x2≤100 x1≤30 x2≤60 X1,X2≥0. ·如何证明目标函数的一个下界? 9
Duality:给目标函数证明上界 max 5�& + 4�' 2�& + �' ≤ 100 �& ≤ 30 �' ≤ 60 �&, �' ≥ 0. • 如何证明目标函数的一个下界? 9

嫩编 Duality::给目标函数证明上界 max 5x1+4x2 2x1+x2≤100(1) x1≤30 (2) x2≤60 (3) x1,X2≥0. 如何证明目标函数的一个上界? ·考虑0×(1)+5×(2)+4×(3) ·考虑3×(1)+0×(2)+1×(3) 考虑×(1)+0×(2)+×(3) 更一般地,考虑y1×(1)+y2×(2)+y3×(3) 10
Duality:给目标函数证明上界 max 5� = × 1 + 0× 2 + ? = ×(3) • … • 更一般地,考虑�<× 1 + �=× 2 + �?×(3) 10

Duality:给目标函数证明上界 min100y1+30y2+60y3 2y1+y2≥5 y1+y3≥4 y1,y2,y3≥0. 5x1+4x2≤(2y1+y2)x1+(y1+y3)x2≤100y1+30y2+60y3 ·拉格朗日乘数法 弱对偶性(weak duality) 11
Duality:给目标函数证明上界 min 100�E + 30�F + 60�G 2�E + �F ≥ 5 �E + �G ≥ 4 �E, �F, �G ≥ 0. 5�E + 4�F ≤ 2�E + �F �E + �E + �G �F ≤ 100�E + 30�F + 60�G • 拉格朗日乘数法 • 弱对偶性 (weak duality) 11