
第4章向量空间 一、n维向量 ()定义 n个有次序的数a,a,,a,所组成的数组称为n维向量,这n个数称为该向量 的n个分量,第i个数a称为第i个分量 分量全为实数的向量称为实向量: 分量全为复数的向量称为复向量。 例如1,2,3…,n) n维实向量 1+2i,2+3i,…,n+(n+1)0) n维复向量 (2)n维向量的表示方法 n维向量写成一行,称为行向量,也就是行矩阵,通常用a,b',a',B等 表示,如: d=(a,a2,…,an) a=1,2,-2,0,-5) B=(0,1-3,4,-8,2,7) n维向量写成一列,称为列向量,也就是列矩阵,通常用a,b,&,B等表 示,如: a a 3 a= 0 B=-4 a=(3.-2,0,62 6 1 注意 1,行向量和列向量总被看作是两个不同的向量: 2,行向量和列向量都按照矩阵的运算法则进行运算:
67 第4章 向量空间 一、n 维向量 (1) 定义 n 个有次序的数 1 2 ,,, n aa a " 所组成的数组称为n 维向量,这n 个数称为该向量 的n 个分量,第i 个数 i a 称为第i 个分量。 分量全为实数的向量称为实向量; 分量全为复数的向量称为复向量。 例如 (1,2,3, , ) " n n 维实向量 (1 2 ,2 3 , , ( 1) ) + + ++ i i nn i " n 维复向量 (2) n 维向量的表示方法 n 维向量写成一行,称为行向量,也就是行矩阵,通常用 ,, , TT T T a b α β 等 表示,如: 1 2 (, , , ) T n a aa a = " (1,2, 2,0, 5) (0,1, 3,4, 8,2,7) T T a = −− = −− β n 维向量写成一列,称为列向量,也就是列矩阵,通常用a b,, , α β 等表 示,如: 1 2 n a a a a ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ # 3 2 2 4 (3, 2,0,6) 0 1 6 T a a β ⎛ ⎞ ⎜ ⎟ ⎛ ⎞ − ⎜ ⎟ ⎜ ⎟ = =− = − ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ 注意 1.行向量和列向量总被看作是两个不同的向量; 2.行向量和列向量都按照矩阵的运算法则进行运算;

间日 3.当没有明确说明是行向量还是列向量时,默认向量类型为列向量 (3)n维向量的加法和数乘运算规律 向量加法:交换律、结合律 数乘向量:结合律、分配律(数的分配、向量的分配) a+0=a a+(-a)=0 lxa=a 二、向量组的线性相关性 ()向量、向量组与矩阵 若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组。 例如矩阵A=(a)_有n个m唯列向量 aa: a. a … a a, a a 向量组2,C称为矩阵的列向量组 类似地,矩阵A=(a)又有m个m维行向量: a1a12…aw a a3 aa aaa…an a 向量组aQ…,称为矩阵A的行向量组
68 1 22 6 4 2 1 30 2 0 2 2 14 31 ⎛ ⎞ ⎛⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ − − ⎜ ⎟ ⎜⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ − − =− + =− ⎝ ⎠ ⎝⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ − 3.当没有明确说明是行向量还是列向量时,默认向量类型为列向量. (3) n 维向量的加法和数乘运算规律 向量加法:交换律、结合律 数乘向量:结合律、分配律(数的分配、向量的分配) 0 ( )0 1 α α α α α α + = + − = × = 二、向量组的线性相关性 (1) 向量、向量组与矩阵 若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组。 例如 ( )m n A nm ij a × 矩阵 有 个 维列向量 = α1 α 2 α j α n 11 12 1 1 21 22 2 2 1 2 j n j n m m mj mn A aa a a aa a a aa a a ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " " " " # ##### " " 1 2 , ,, . n 向量组 称为矩阵 的列向量组 α α α " A , ( )m n A mn ij a × 类似地 矩阵 又有 个 维行向量: = 11 12 1 21 22 2 1 2 1 2 n n i i in m m mn A aa a aa a aa a aa a ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " " # #"# " # #"# " 1 2 T T T i T m α α α α 向量组 1 2 , ,, TT T α α α " m 称为矩阵 A 的行向量组
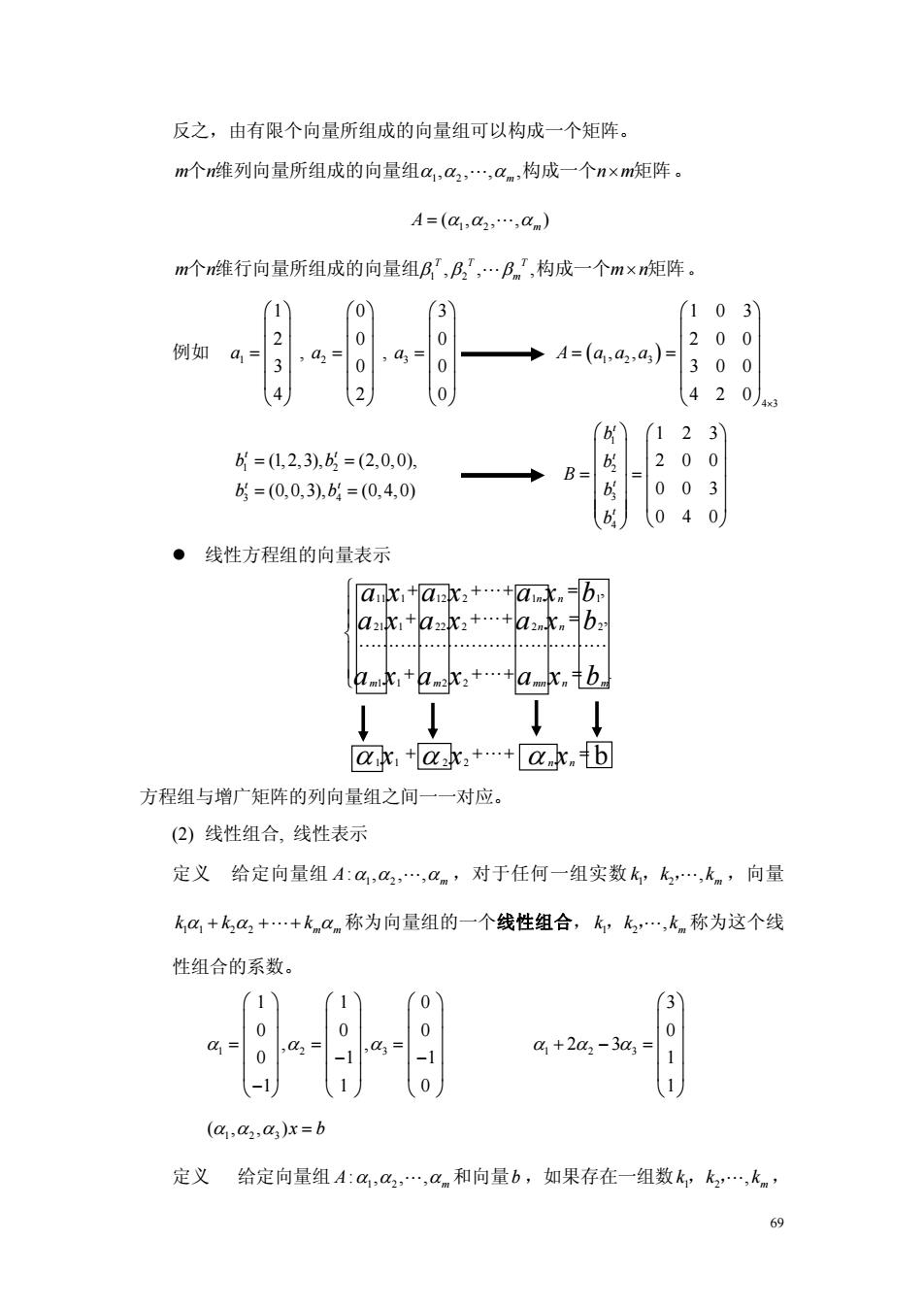
反之,由有限个向量所组成的向量组可以构成一个矩阵。 m个维列向量所组成的向量组a,a,,a,构成一个nxm矩阵。 A=(g,42,…,a)) m个n维行向量所组成的向量组BT,E',…BT,构成一个mxn矩阵。 1 0 103 例如a340 +A=(a,2,a) 200 ,4 0 300 4 420 )123 6=0,2,3),=(2,0,0) b=(0,0,3),b=(0,4,0) B= 6 003 (040 ●线性方程组的向量表示 ax,+ak,++a水.br a2k1+a2k2+…+a2nknb2 ……………… hmk+hmk,+…+a.x.tb ↓ ak,+ak:++a.k.tb 方程组与增广矩阵的列向量组之间一一对应。 (2)线性组合,线性表示 定义给定向量组A:4,a,…,,对于任何一组实数k,k,…,k,向量 ka+k2+…+kan称为向量组的一个线性组合,k,k,…,k称为这个线 性组合的系数。 1 0 3 0 %+2a42-34= 0 1 1 0 (a.az.a3)x=b 定义给定向量组A:a,,…,an和向量b,如果存在一组数k,k…,km: 69
69 反之,由有限个向量所组成的向量组可以构成一个矩阵。 1 2 ,,, , m n nm 个 维列向量所组成的向量组 构成一个 矩阵 α α α " m × 。 1 2 (, , , ) A = α α α " m 1 2 ,, , TT T m n mn 个 维行向量所组成的向量组 构成一个 矩阵 ββ β " m × 。 例如 123 103 200 , , 300 420 aaa ⎛⎞ ⎛⎞ ⎛⎞ ⎜⎟ ⎜⎟ ⎜⎟ === ⎝⎠ ⎝⎠ ⎝⎠ ( ) 123 4 3 103 200 , , 300 420 A aaa × ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ 1 2 3 4 (1, 2,3), (2,0,0), (0,0,3), (0, 4,0) t t t t b b b b = = = = 1 2 3 4 123 200 003 040 t t t t b b B b b ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ z 线性方程组的向量表示 11 1 12 2 1 1 21 1 22 2 2 2 11 2 2 , , . n n n n m m mn n m ax ax ax b ax ax ax b ax ax ax b ⎧ + ++ = ⎪ ⎪ + ++ = ⎨ ⎪ ⎪ + ++ = ⎩ " " """""""""""""" " 11 2 2 α xx x + ++ = α α " n n b 方程组与增广矩阵的列向量组之间一一对应。 (2) 线性组合, 线性表示 定义 给定向量组 1 2 :,,, A α α α " m ,对于任何一组实数 1 2 , m kk k , , ,向量 " 11 2 2 m m kk k α + ++ α α " 称为向量组的一个线性组合, 1 2 , m kk k , , 称为这个线 " 性组合的系数。 123 110 000 , , 0 11 11 0 ααα ⎛⎞ ⎛⎞ ⎛⎞ ⎜⎟ ⎜⎟ ⎜⎟ === − − ⎝⎠ ⎝⎠ ⎝⎠ − 123 3 0 2 3 1 1 ααα ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ +−= ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ 123 (, , ) α α α x = b 定义 给定向量组 1 2 :,,, A α α α " m 和向量b ,如果存在一组数 1 2 , m kk k ,, ,

使 b=ka+k42+…kan 则向量b是向量组A的线性组合,这时称向量b能由向量组A线性表示或线 性表出。 即线性方程组 a1+,g3+…+xam=b 有解。 定理n维向量B可由n维向量组a,凸,,a线性表示 一线性方程组xa,+x,a4+…+xan=B有解 白矩阵A=(a,心2,…,an)的秩等于矩阵A=(a,a2,…,a,)的秩。 向量b能由向量组A线性线性表示的充分必要条件是矩阵A=(a,,,a)的秩 等于矩阵B=(a,a2,…,&,B)的秩。 (3)线性相关性的概念 定义给定向量级A=(@,a,…,an)。如果存在不全为零的数k,k…,kn,使 k4+k凸+…+kan=0,则称向量组A是线性相关的,否则称它线性无关。 注意1.若a,4,…,a。线性无关,则只有当=…=入,=0时,才有 4+a2+…+an=0成立。 2.对于任一向量组,不是线相关就是线性无关。 3.向量组只包含一个向量a时,若a=0则说a线性相关,若a≠0, 则说α线性无关。 4.包含零向量的任何向量组是线性相关的。 5.对于含有丙个向量的向量组,它线性相关的充要条件是两向量的分量 对应成比例,几何意义是两向量共线;三个向量相关的几何意义是三向量共面。 ·线性相关性在线性方程组中的应用 若方程组中有某个方程是其余方程的线性组合时,这个方程就是多余的,这是称
70 使 11 2 2 m m bk k k = α + + α α " 则向量b 是向量组 A的线性组合,这时称向量b 能由向量组 A 线性表示或线 性表出。 即线性方程组 11 2 2 m m xα + x xb α α ++ = " 有解。 定理 n 维向量β 可由n 维向量组 1 2 ,,, α α α " m 线性表示 ⇔ 线性方程组 11 2 2 m m xx x α + ++ = α αβ … 有解 ⇔ 矩阵 1 2 (, , , ) A = α α α " m 的秩等于矩阵 1 2 (, , , ,) A = α α αβ " m 的秩。 向量b 能由向量组 A线性线性表示的充分必要条件是矩阵 1 2 (, , , ) A = α α α " m 的秩 等于矩阵 1 2 (, , , ,) B = α α αβ " m 的秩。 (3) 线性相关性的概念 定义 给定向量级 1 2 (, , , ) A = α α α " m 。如果存在不全为零的数 1 2 , m kk k , , ,使 " 11 2 2 0 m m kk k α + ++ = α α " ,则称向量组 A是线性相关的,否则称它线性无关。 注 意 1. 若 1 2 ,,, α α α " n 线性无关,则只有当 1 0 λ ="= = λn 时,才有 11 2 2 0 λα λα λα + ++ = " n n 成立。 2.对于任一向量组,不是线相关就是线性无关。 3.向量组只包含一个向量α 时,若α = 0 则说α 线性相关,若α ≠ 0 , 则说α 线性无关。 4.包含零向量的任何向量组是线性相关的。 5.对于含有丙个向量的向量组,它线性相关的充要条件是两向量的分量 对应成比例,几何意义是两向量共线;三个向量相关的几何意义是三向量共面。 z 线性相关性在线性方程组中的应用 若方程组中有某个方程是其余方程的线性组合时,这个方程就是多余的,这是称

方程组(各个方程)是线性相关的:当方程组中没有多余方程,就称该方程组(各 个方程)线性无关(或线性独立)。 结论向量组A线性相关就是齐次线性方程组x%,+xa,++xan=0,即 Ax=0有非零解。其中A=(a,,…am)。 例己知 试讨论向量组a,a,a的线性相关性。 解方法】判断齐次线性方程组是否有非零解 方法2直接由向量组形成的矩阵判断该矩阵所对应的齐次方程组解的情况。 例已知向量组a,a,a线性无关,=a+a2,b,=a,+a,=a,+a,试 证b,b2,b,线性无关。 证设有x,x,x,使 xb+xb+xb,=0 即x(a+a,)+x(a+a)+x(a,+a)=0 亦即 (x+x)a+(x+x2)a2+(x+x)a3=0 因aa,a,线性无关,故有 [x+x=0, 了+x3=0, +=0. 由于此方程组的系数行列式 10 110-2≠0 011 故方程组只有零解x=x2=x=0,所以向量组,b,b线性无关。 性质若向量组在a,a,…,an线性相关,则向量组B:a,…,a,C也线性相 11
71 方程组(各个方程)是线性相关的;当方程组中没有多余方程,就称该方程组(各 个方程)线性无关(或线性独立)。 结论 向量组 A 线性相关就是齐次线性方程组 11 2 2 0 m m xx x α + α α ++ = " ,即 A 0 x = 有非零解。其中 1 2 (, , ) A = α α α " m 。 例 已知 12 3 102 124 157 αα α ⎛⎞ ⎛ ⎞ ⎛ ⎞ ⎜⎟ ⎜ ⎟ ⎜ ⎟ == = ⎝⎠ ⎝ ⎠ ⎝ ⎠ ,,, 试讨论向量组 123 α , , α α 的线性相关性。 解 方法 1 判断齐次线性方程组是否有非零解。 方法 2 直接由向量组形成的矩阵判断该矩阵所对应的齐次方程组解的情况。 例 已知向量组 123 α , , α α 线性无关, 112 b =α +α , 2 23 b =α +α , 3 31 b = + α α ,试 证 123 bbb , , 线性无关。 证 设有 123 x , , x x ,使 11 2 2 33 xb xb xb + + = 0 即 11 2 22 3 33 1 xx x ( ) α ++ ++ += α αα αα ( ) ( )0 亦即 1 31 1 2 2 2 33 ( )( )( ) 0 xx xx xx + ++ ++ = α α α 因 , , 线性无关,故有 α123 α α 1 3 1 2 2 3 0, 0, 0. x x x x x x ⎧ + = ⎪ ⎨ + = ⎪ ⎩ + = 由于此方程组的系数行列式 101 110 20 011 = ≠ 故方程组只有零解 123 xxx === 0 ,所以向量组 123 bbb , , 线性无关。 性质 若向量组 1 2 ,,, A: 线性相关,则向量组 α α α " m 1 1 :,, , B α " α α m m+ 也线性相

关;反言之,若向量组B线性无关,则向量组A也线性无关。 (部分相关,则整体相关:整体无关,则部分无关)。 (4)线性相关性的判定 定理对于向量组在a,a,…,an,记A(g,a4,…,a),则 1.A线性相关的充要条件是R(4)n时,m个n维向量组成的向量组a,4,,a。一定线性相关。 推论3设有两个向量组 T:c,=(a42…,a)',U=1,2,m) 7:月=a4,0g4…,ay,0=l2…,m 若向量组T线性无关,则向量组T,也线性无关。 若向量组T,线性相关,则向量组T也线性相关。 例n维向量组 g=(1,0…,0),e2=(01…,0,…,en=(0,0…,0 称为n维单位坐标向量组,讨论其线性相关性, 解法1n维单位坐标向量组构成的矩阵E=(e,e,,e,)是n阶单位矩阵。即 R(E)等于向量组中向量个数,故由定理知此向量组是线性无关的
72 关;反言之,若向量组 B 线性无关,则向量组 A也线性无关。 (部分相关,则整体相关;整体无关,则部分无关)。 (4) 线性相关性的判定 定理 对于向量组 1 2 ,,, A: ,记 α α α " m A=(α1 2 ,,, α α " m ) ,则 1. A线性相关的充要条件是 R( ) A m 时,m 个n 维向量组成的向量组 2 ,,, α1 α α " m一定线性相关。 推论 3 设有两个向量组 1 12 : ( , , , ) ,( 1, 2, , ) T T aa a j m α j j j rj = = " … 2 12 1 : ( , , , , , , ) ,( 1, 2, , ) T T aa aa a j m β j j j rj r j nj = = "" … + 若向量组T1线性无关,则向量组T2 也线性无关。 若向量组T2 线性相关,则向量组T1也线性相关。 例 n 维向量组 1 2 ( )( ) ( ) 1,0, ,0 , 0,1, ,0 , 0,0, ,1 TT T n ee e == = " "" " , 称为 维单位坐标向量组 讨论其线性相关性 n , . 解 法 1 n 维单位坐标向量组构成的矩阵 1 2 (, , , ) E ee e = " n 是n 阶单位矩阵。即 R( ) E 等于向量组中向量个数,故由定理知此向量组是线性无关的

法2利用线性相关性的定义。 0) 2 例设a= =2 a4试讨论向量组a,a,a,及a,a,的线性相关 ( 5 7 性。 分析对矩阵a,a,a,施行行初等变换,化为行阶梯形矩阵,便可同时看出 矩阵(a,a,a)及(a,a的秩,利用定理即可得出结论 10引 解(a,,)=124 i57000 R(a,a2,a,》=2<3,向量组a,a,a,线性相关: R(a,4,)》=2,向量组a,a,线性无关 定理向量组a,a2,an(m之2)饯性相关的充要条件是a,a2,an中至少 有一个向量可由其它m-1个向量线性表示 证明必要性设4,a,…,an线性相关,则存在不全为零的数k,k,…,k,使得 ka1+k342+…+kam=0 不妨设k≠0, 即a,可由a,a,…&n线性表示 充分性设α,a,,a中至少有一个向量可由其他m-1个向量线性表示, 不妨设an可由a,a,…,a表示,则 a=ka+kaz+.+km-m- 移项得 ka+kaz+...+kma-a=0 所以,存在k,k,…,k1,-1不全为0
73 法 2 利用线性相关性的定义。 例 设 12 3 102 124 157 αα α ⎛⎞ ⎛ ⎞ ⎛ ⎞ ⎜⎟ ⎜ ⎟ ⎜ ⎟ == = ⎝⎠ ⎝ ⎠ ⎝ ⎠ ,,,试讨论向量组 123 12 α ,, , αα αα 及 的线性相关 性。 分析 123 对矩阵 施行行初等变换 ( , , ), , α α α 化为行阶梯形矩阵, 便可同时看出 123 12 矩阵 及 的秩 利用定理即可得出结论 (, , )(, ) , . α αα αα 解 123 102 102 (, , ) 124 022 157 000 ~ r ααα ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ = ⎝ ⎠⎝ ⎠ … 123 123 ∴R(( , , )) 2 3, , , α αα ααα = < 向量组 线性相关; 12 12 R(( , )) 2, , . α α αα = 向量组 线性无关 定理 12 12 , , , ( 2) , , , 向量组 线性相关的充要条件是 中至少 α α α αα α … … m m m ≥ 有一个向量可由其它 个向量线性表示 m −1 . 证明 必要性 1 2 ,,, , 设 线性相关 α α α " m 1 2 ,,, , m 则存在不全为零的数 使得 kk k " 11 2 2 0, m m kk k α + α α ++ = " 1 不妨设k ≠ 0, 2 3 1 23 11 1 ( ) ( ) ( ) , m m k k k kk k 则 α =− +− + +− αα α " 1 23 ,, . 即 可由 线性表示 α αα α " m 充分性 1 2 ,,, 设 中至少有一个向量可由其他 α α α " m m −1个向量线性表示, 不妨设α m可由 12 1 ,,, α α α " m− 表示,则 m mm 11 2 2 1 1 α = kk k αα α + ++ " − − 移项得 11 2 2 1 1 0 mm m kk k α + α αα ++ − = " − − 所以,存在 12 1 , , , ,1 m kk k " − − 不全为 0

所以a,a,…,an线性相关 定理设向量组A:a,a,…,an线性无关,而向量组B:a,,a,b线性相关,则 向量b必能由向量组A线性表示,且表示式是唯一的。 证明组B:a,…,a,b线性相关 .存在不全为零的数k,…,k,k,使得 ka+k凸+…+knan+kb=0 a,4,,Q线性无关k≠0, b=会4+会a+4(是 设b=,a+a2+…+九4n b=4a+山a3+…+4naw (4-)a+(42-2)a2+…+(4n-n)an=0, a,4,…,a线性无关4=,…,4n= 三、向量组的秩 1.向量组的等价 定义设有两个向量组A:a,a2,…,an与B:月,B,…,Bn若向量组B中 的向量均可由向量组A线性表示,则称向量组B可由向量组A线性表示: 若向量组A与向量组B可以相互线性表示,则称向量组A与向量组 B等价 性质:反身性、对称性、传递性 线性表示中的系数矩阵K 设有两个向量组A:a,a2,,an;B,b,…,b,B能由A线性表示,即对每个 向量b,=1,2,…,S)存在数k,k…k’使
74 所以 1 2 ,,, α α α " m线性相关 定理 设向量组 1 2 :,,, A α α α " m 线性无关,而向量组 1 :,, , B m α " α b 线性相关,则 向量b 必能由向量组 A线性表示,且表示式是唯一的。 证明 1 :,, , , ∵ " 组 线性相关 B b α α m 1, , ,, m ∴存在不全为零的数 使得 k kk " 11 2 2 0 m m k k k kb α + α α ++ + = " 1 2 , , , , 0, m ∵ " α α α 线性无关 ∴k ≠ 1 2 1 2 ( ) ( ) ( ); m m k k k b kk k ∴ =− +− + +− α α α " 11 2 2 , m m 设b = λα λα λ α + ++ " 11 2 2 , m m b = + ++ μ α μα μ α " 1 11 2 2 2 ( ) ( ) ( ) 0, μ − λα μ λα μ λ α + − ++ − = " m mm 12 1 1 ,,, , ,, . ∵" " α α α μλ μ λ m mm 线性无关 ∴ = = 三、向量组的秩 1. 向量组的等价 定义 设有两个向量组 1 2 : , , , A α α α " m 1 2 : , , , . 与 若向量组 B β β β " n B 中 的向量均可由向量组 A 线性表示, 则称向量组 B 可由向量组 A 线性表示; 若向量组 A 与向量组 B 可以相互线性表示, 则称向量组 A 与向量组 B 等价. 性质:反身性、对称性、传递性 线性表示中的系数矩阵 K 设有两个向量组 1 2 12 : , , , ;: , , , A Bb b b α α α " " m s ,B 能由 A线性表示,即对每个 向量 ( 1,2, , ) j bj s = " 存在数 1 2 , , j j mj kk k " ,使

b=ka+k42+…+kman b2=k2%+k2a3+…+km20 b,=ka1+k22+…+kmam b,=k,a1+k.%2+…+kma (6,6,…,b)=(a,4,…,an)K kk2…ka kk2…k K- k1k2…k 若矩阵C=AB,设Cnm,A,Bn bb2…bn bb2…bm 则C的列向量组能由的列向量组线性表示,B为这一表示的系数矩阵 类似地,若Cn=AnBn aa2…a)B y …a八Br C的行向量组能由的行向量组线性表示,A为这一表示的系数矩阵 定理若向量组T:,,,可由向量组2:月,月,,B线性表示,且m>n 则T线性相关。 推论1若向量组T:4,4,,an可由向量组T,:月,月,…,B线性表示,且T线性 无关,则m≤n。 推论2若两个线性无关向量组等价,则它们所包含的向量的个数相等
75 1 11 1 21 2 1 2 12 1 22 2 2 11 2 2 11 2 2 m m m m j j j mj m s s s ms m bk k k bk k k bk k k bk k k α α α α α α α α α α α α = + ++ = + ++ = + ++ = + ++ " " """" " """" " 12 1 2 (, , , ) ( , , , ) s m bb b K " " = α α α 11 12 1 21 22 2 1 2 s s m m ms kk k kk k K kk k ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " " ## # " , ,,, 若矩阵 设 C AB C A B = mn ms sn × ×× 11 12 1 21 22 2 12 1 2 1 2 (,,,)(, ,, ) n n n s s s sn bb b bb b cc c bb b αα α ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " " " " ## # " 则 的列向量组能由 的列向量组线性表示 为这一表示的系数矩阵 CA B, . , 类似地 若C AB mn ms sn × ×× = 1 1 11 12 1 2 2 21 22 2 1 2 T T s T T s T T m s m m ms aa a aa a aa a γ β γ β γ β ⎛⎞ ⎛⎞ ⎛ ⎞ ⎜⎟ ⎜⎟ ⎜ ⎟ = ⎝⎠ ⎝⎠ ⎝ ⎠ " " # # ## # " CB A 的行向量组能由 的行向量组线性表示 为这一表示的系数矩阵 , . 定理 若向量组 1 2 :,,, T α1 α α " m 可由向量组 2 2 :,,, T β1 β β " n线性表示,且m n > , 则T1线性相关。 推论 1 若向量组 1 2 :,,, T α1 α α " m 可由向量组 2 2 :,,, T β1 β β " n线性表示,且T1线性 无关,则m n ≤ 。 推论 2 若两个线性无关向量组等价,则它们所包含的向量的个数相等

定理矩阵A经初等行变换化为矩阵B,则A与B的任何对应的列向量构成的 列向量组有相同的线性组合关系。 2.最大线性无关组 定义设有向量组A:C,如果在向量组中存在r个向量a,a2,…,a,满足 ()向量组A,a,a,…,a,线性无关 (2)向量组4中任意r+1(若有个向量线性相关, 则称向量组4是向量组的一个最大线性无关组,(简称最大无关组) 定义向量组A,中所含向量的个数称为向量组的秩 向量组A:a,a,…,a的秩记作R(a,a,…,an),R(4) 只含0响量的向量组的秩规定为0 证明:a,4,a,是向量组的一个最大无关组 (100100 证明A=(a,a,a4)=010-010 111(001 ∴R(4)=3,∴向量组a,4,a,线性无关 又:任意4个向量构成的向量组线性相关, 4,4,a,是一个最大无关组 3.矩阵的秩与向量组的秩的关系 定理矩阵的秩等于它的列向量组的秩也等于它的行向量组的秩, 证设A=(a,4,,abR(A)=r,并设阶子式D,≠0.则D,所在的r列线性无关 又由A中所有r+1(若有)阶子式均为零,知A中任意r+I(若有)个列向量都 线性相关
76 定理 矩阵 A 经初等行变换化为矩阵 B,则 A 与 B 的任何对应的列向量构成的 列向量组有相同的线性组合关系。 2. 最大线性无关组 定义 1 2 :, ,,,, 设有向量组 如果在向量组 中存在 个向量 满足 A Ar αi r αα α " 0 12 (1) : , , , ; 向量组 线性无关 A α α α " r (2) 1( ) ; 向量组 中任意 若有 个向量线性相关 A r + 0 则称向量组 是向量组 的一个最大线性无关组,简称最大无关组 A A ( ). 定义 0 向量组 中所含向量的个数 称为向量组的秩 A r . 12 12 : , , , ( , , , ), ( ). 向量组 的秩记作 A a a a Ra a a RA " " m m 只含 向量的向量组的秩规定为 0 0. 例 设 123456 1 3 0 0 2 12 0 , 5 , 1 , 0 , 1 , 71 1 4 1 1 2 29 aaaaaa ⎛⎞ ⎛⎞ ⎛⎞ ⎛⎞ ⎛⎞ ⎛ ⎞ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟ ⎜ ⎟ ====== ⎝⎠ ⎝⎠ ⎝⎠ ⎝⎠ ⎝⎠ ⎝ ⎠ 134 证明: 是向量组 的一个最大无关组 aaa A ,, . 证明 134 100 100 (, , ) 0 1 0~0 1 0 111 001 A aaa ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ = = ⎝ ⎠⎝ ⎠ ∵ 134 ∴RA a a a ( ) 3, , , , = ∴向量组 线性无关 又 任意 个向量构成的向量组线性相关 ∵ 4 , 134 ∴aaa ,, . 是一个最大无关组 3. 矩阵的秩与向量组的秩的关系 定理 矩阵的秩等于它的列向量组的秩 也等于它的行向量组的秩 , . 证 A ( , , , ), (A) , 0. 1 2 m r 设 并设 阶子式 = =≠ aa a R r r D " . 则 所在的 列线性无关 D r r 又由 中所有 若有 阶子式均为零 知 中任意 若有 个列向量都 A 1( ) , A 1( ) r r + + 线性相关