
图的连通性 离散数学一图论初步 南京大学计算机科学与技术系
图的连通性 离散数学─图论初步 南京大学计算机科学与技术系

急售房 内容提要 ●通路与回路 。通路与同构 无向图的连通性 ●连通度 。2-连通图 ●有向图的连通性 。无向图的定向 2
内容提要 通路与回路 通路与同构 无向图的连通性 连通度 2-连通图 有向图的连通性 无向图的定向 2

售嘉 通路的定义 ·定义:图G中从v到yn的长度为n的通路是G的n条边 e1,en的序列,满足下列性质 。存在y,∈V(0<i<m),使得ya和y是e的两个端点(1≤i达n)。 ·相关点 。回路:起点与终点相同,长度大于0。 ·不必区分多重边时,可以用相应顶点的序列表示通路。 ●长度为0的通路由单个顶点组成。 简单通路:边不重复,即,i,j,j→; ●初级通路:点不重复,亦称为“路径” 3
通路的定义 定义:图G中从v0到vn的长度为n的通路是G的n条边 e1 ,…, en的序列,满足下列性质 存在viV (0in), 使得vi-1和vi是ei的两个端点 (1in)。 相关点 回路:起点与终点相同,长度大于0。 不必区分多重边时,可以用相应顶点的序列表示通路。 长度为0的通路由单个顶点组成。 简单通路:边不重复,即,i, j, ij ei ej 初级通路:点不重复,亦称为“路径” 3
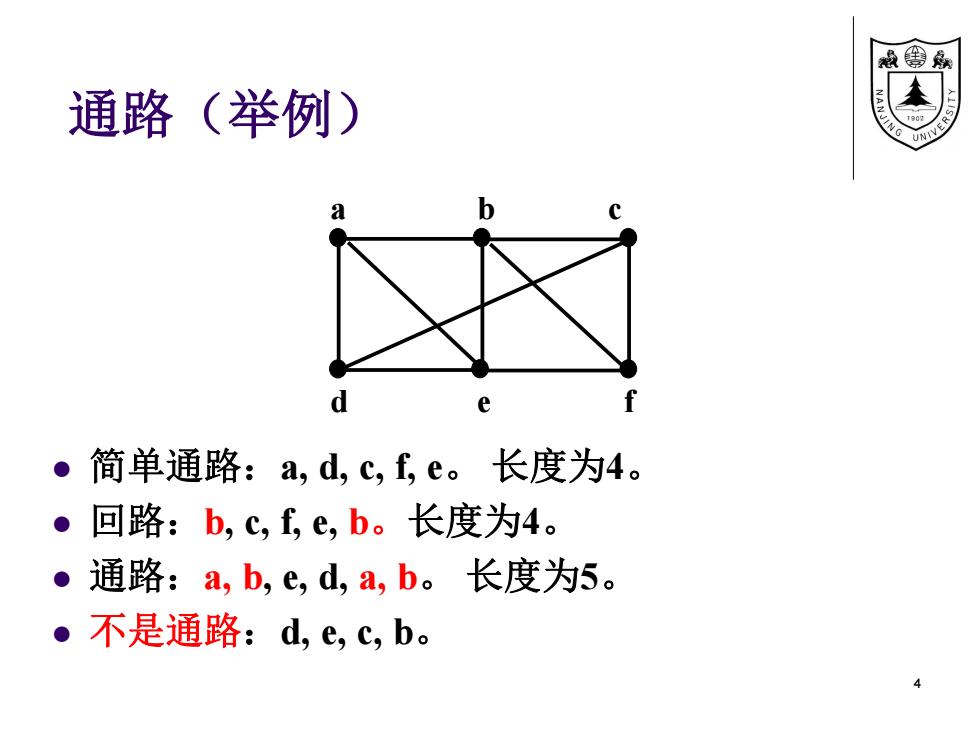
线兔 通路(举例) d ·简单通路:a,d,C,fe。长度为4。 ·回路:b,c,f,e,b。长度为4。 ●通路:a,b,e,d,a,b。长度为5。 。不是通路:d,e,c,b
通路(举例) 简单通路:a, d, c, f, e。 长度为4。 回路:b, c, f, e, b。长度为4。 通路:a, b, e, d, a, b。 长度为5。 不是通路:d, e, c, b。 4 a b c d e f

售嘉 通路的定义(有向图) 定义:有向图G中从v,到y的长度为n的通路是G的n 条边e,en的序列,满足下列性质 ·存在y,∈V(0<i<n),使得y和y,分别是e的起点和终点(1≤i≤)。 ·相关点 ·回路:起点与终点相同,长度大于0。 ·不必区分多重边时,可以用相应顶点的序列表示通路。 ·长度为0的通路由单个顶点组成。 。简单通路:边不重复,即,i,j,j→ee 5
通路的定义(有向图) 定义:有向图G中从v0到vn的长度为n的通路是G的n 条边e1 ,…, en的序列,满足下列性质 存在viV (0in), 使得vi-1和vi分别是ei的起点和终点 (1in)。 相关点 回路:起点与终点相同,长度大于0。 不必区分多重边时,可以用相应顶点的序列表示通路。 长度为0的通路由单个顶点组成。 简单通路: 边不重复,即,i, j, ij ei ej 5
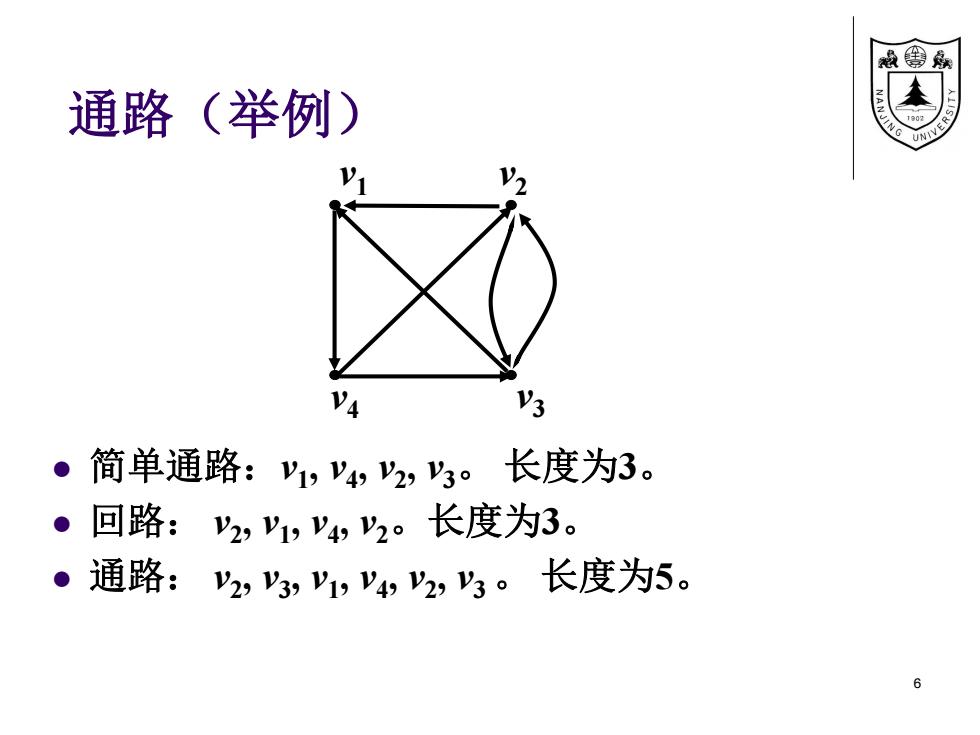
线兔 通路(举例) VA V3 ·简单通路:1,4,2,3。长度为3。 ·回路:2,1,V4,2。长度为3。 ·通路:2,3,1,4,2,3。长度为5。 6
通路(举例) 简单通路:v1 , v4 , v2 , v3。 长度为3。 回路: v2 , v1 , v4 , v2。长度为3。 通路: v2 , v3 , v1 , v4 , v2 , v3 。 长度为5。 6 v1 v2 v v4 3

款嘉 通路与同构 。设图G的邻接矩阵为A ●(A):到y的长度为k的通路个数 ●(A:y到,的长度为k的回路个数 。同构图的不变量:长度为k的回路的存在性
通路与同构 设图G的邻接矩阵为A (Ak )i,j: vi到vj的长度为k的通路个数 (Ak )i,i: vi到vi的长度为k的回路个数 同构图的不变量:长度为k的回路的存在性。 7
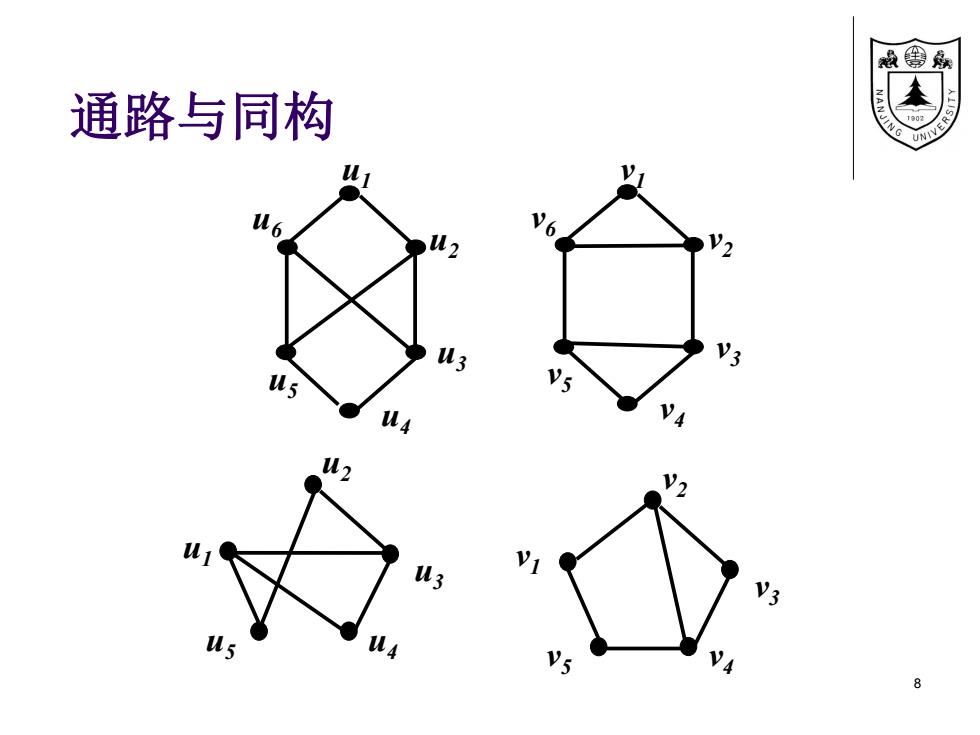
线兔 通路与同构 u3 V: us v5 u3 Vs 8
通路与同构 8 u6 u2 u1 u5 u3 u4 v6 v2 v1 v5 v3 v4 u2 u5 u1 u3 u4 v2 v5 v1 v3 v4
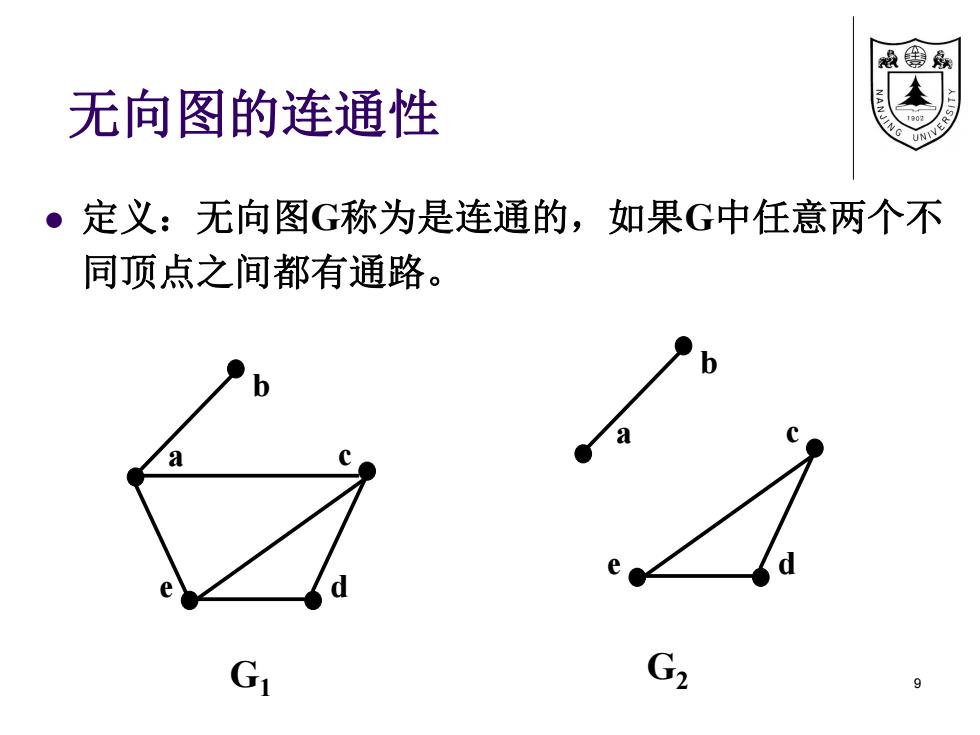
款线嘉 无向图的连通性 。定义:无向图G称为是连通的,如果G中任意两个不 同顶点之间都有通路。 9 G2 9
无向图的连通性 定义:无向图G称为是连通的,如果G中任意两个不 同顶点之间都有通路。 9 a c b e d a c b e d G1 G2

线感 连通分支 ●连通分支 。极大连通子图 。每个无向图是若干个互不相交的连通分支的并。 。“顶点之间存在通路”是一个等价关系,任一等价类上的 导出子图即为一个连通分支。 ●若图G中存在从u到v的通路,则一定有从u到v的简 单通路。 ·证明:最短通路必是简单的,事实上,它没有重复顶点。 10
连通分支 连通分支 极大连通子图 每个无向图是若干个互不相交的连通分支的并。 “顶点之间存在通路”是一个等价关系,任一等价类上的 导出子图即为一个连通分支。 若图G中存在从u到v的通路,则一定有从u到v的简 单通路。 证明:最短通路必是简单的,事实上,它没有重复顶点。 10