
☒有京大赞 NANJING UNIVERSITY 离散数学 Discrete Mathematics 偏序与偏序格 南京大学计算机科学与技术系
偏序与偏序格 离 散 数 学 Discrete Mathematics 南京大学计算机科学与技术系

&嘉 回顾 ·关系的闭包 ·闭包的定义 。 闭包的计算公式 ·传递闭包的Warshall?算法 等价关系 ·等价类 ·划分
回顾 2 • 关系的闭包 • 闭包的定义 • 闭包的计算公式 • 传递闭包的Warshall算法 • 等价关系 • 等价类 • 划分
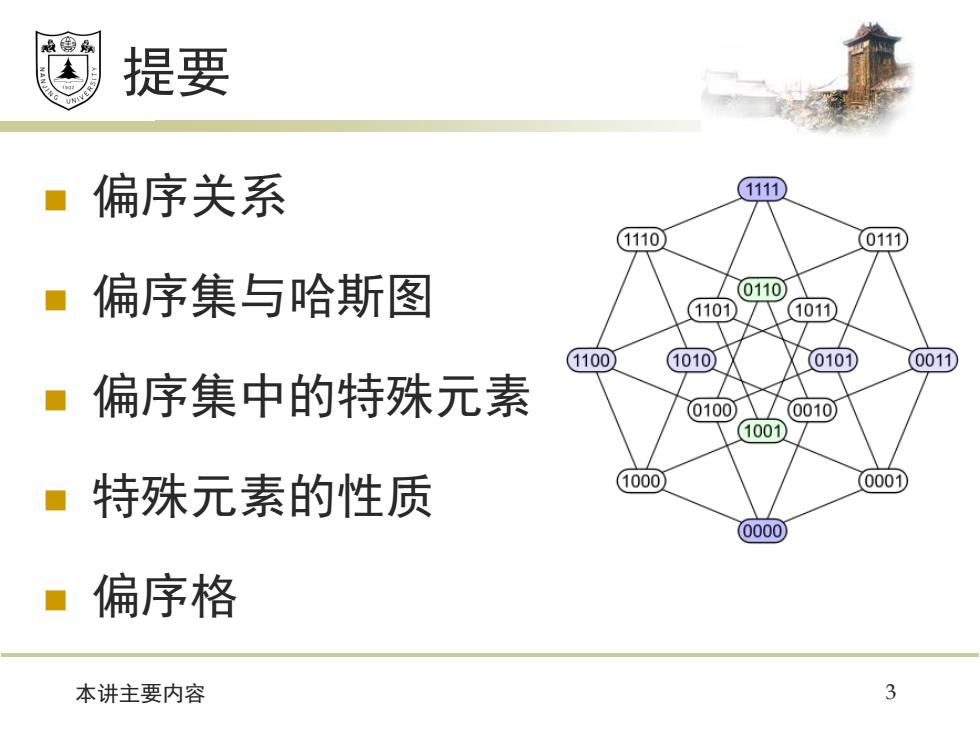
&原 提要 ·偏序关系 (1111 1110 0111 ■偏序集与哈斯图 0110 1101T1011 1100 1010】 0101 001① ■偏序集中的特殊元素 0100 0010 10017 ■特殊元素的性质 1000】 (0001) (0000 ·偏序格 本讲主要内容 3
提要 本讲主要内容 3 偏序关系 偏序集与哈斯图 偏序集中的特殊元素 特殊元素的性质 偏序格

偏序关系(Partial Order) 定义(偏序关系):非空集合A上的自反、 反对称和传递的关系称为A上的偏序关系, 记为:≤ 设≤为偏序关系,若(a,b)∈≤,则记为a≤b 读作“a小于或等于b” 实例 集合A上的恒等关系I4是A上的偏序关系 小于或等于关系,整除关系和包含关系也是相应集合上的 偏序关系 偏序关系
偏序关系(Partial Order) 偏序关系 4

& 偏序关系(续) 定义: 设R为非空集合A上的偏序关系, x,y∈A,x与y可比台xyVy<x 任取两个元素x和y,可能有下述几种情况发生: x<y(或y<x),x=少,x与y不是可此的 定义:R为非空集合A上的偏序关系 Vxy EA,x与y都是可比的,则称R为全序(或线序) 实例:数集上的小于或等于关系是全序关系 整除关系不是正整数集合上的全序关系 定义:xy∈A,如果x<y且不存在z∈A使得x<z<y,则称y覆盖x. 例如{1,2,4,6}集合上的整除关系,2覆盖1,4和6覆盖2.但4不 覆盖1 偏序关系 5
偏序关系(续) 偏序关系 5 : : :

&易 偏序集(poset)与哈斯图 1. 偏序集 定义: 集合A和A上的偏序关系<一起叫做偏序集,记作(A,≤)】 实例: 整数集合Z和数的小于或等于关系≤构成偏序集(Z,≤) 集合A的幂集P(4)和包含关系R构成偏序集(P(4),R)》 2.哈斯图 利用偏序关系的自反、反对称、传递性进行简化的关系图 特点: 。每个结点没有环 两个连通的结点之间的序关系通过结点位置的高低表示,位置 低的元素的顺序在前 具有覆盖关系的两个结点之间连边 偏序集与哈斯图 6
偏序集(poset)与哈斯图 偏序集与哈斯图 6 : ( ) ( ) ( )

& 偏序集 例:证明(P(A),S)为全序当且仅当|A≤1 证明: (1)“←”: Case1:A=0,P(A)={0},(P(A),)为全序 Case2:A=1,设A={a},P(A={0,{a},(P(A),)为全序 “→”:只需证A≥2时,(P(A),)非全序 A≥2.可取a,b∈A,a≠b {a{b}不可比∴.(P(A),)非全序 偏序集 7
偏序集 偏序集 7 {a} {b}不可比

& 偏序集(续) 例:字典序(lexicographic order)与偏序集 0 给定两个偏序集(A,≤4)与(B,≤B),在A×B 上定义新关系“≤”: (a,b)≤(c,d)台a<cV(a=c∧b≤d) ■ 另证,4×B,)是-个偏序集。A 偏序集 8
偏序集(续) 例:字典序(lexicographic order)与偏序集 给定两个偏序集 𝐴, ≼𝐴 与 (𝐵, ≼𝐵) ,在 𝐴 × 𝐵 上定义新关系“≼”: 𝑎, 𝑏 ≼ 𝑐, 𝑑 ⇔ 𝑎 ≺ 𝑐 ∨ (𝑎 = 𝑐 ∧ 𝑏 ≼ 𝑑) 易证, (𝐴 × 𝐵, ≼) 是一个偏序集。 偏序集 8

&原 偏序集(续) 例:在字典中“part”和“park”两个单词 的顺序如何? Dictionary Thesaurus 定义全序集(英文字母表)S={a,b,c,…,z: 元素满足线序关系Q≤b,b≤C,…,y≤z,令 S4=S×S×S×S,易见,(p,a,r,t)∈S4, (p,a,T,k)∈S4;根据字典序,park≤part 偏序集 9
偏序集(续) 偏序集 9
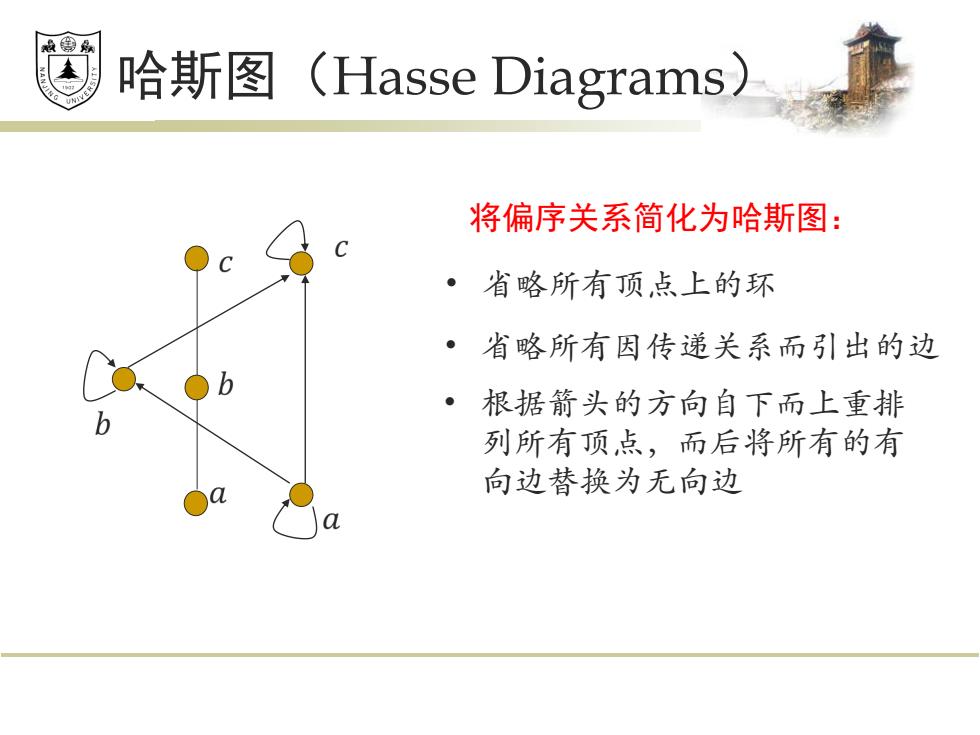
&是 哈斯图(Hasse Diagrams) 将偏序关系简化为哈斯图: ·省略所有顶点上的环 ·省略所有因传递关系而引出的边 ·根据箭头的方向自下而上重排 列所有顶点,而后将所有的有 向边替换为无向边
哈斯图(Hasse Diagrams) 将偏序关系简化为哈斯图: • 省略所有顶点上的环 • 省略所有因传递关系而引出的边 • 根据箭头的方向自下而上重排 列所有顶点,而后将所有的有 向边替换为无向边