
生成树 离散数学一树 南京大学计算机科学与技术系
生成树 离散数学─树 南京大学计算机科学与技术系

内容提要 ·生成树 ·深度优先搜索 。广度优先搜索 ●有向图的深度优先搜索 ·回溯 ·最小生成树算法
内容提要 生成树 深度优先搜索 广度优先搜索 有向图的深度优先搜索 回溯 最小生成树算法

生成树 ●定义:若图G的生成子图是树,则该子图称为G 的生成树。 ·无向图G连通当且仅当G有生成树 。证明(充分性显然): →注意:若G是有简单回路的连通图,删除回路上的 一条边,G中的回路一定减少。(因此,用“破圈 法”总可以构造连通图的生成树) ·简单无向图G是树当且仅当G有唯一的生成树。 。注意:G中任一简单回路至少有三条不同的边
生成树 定义:若图G的生成子图是树,则该子图称为G 的生成树。 无向图G连通 当且仅当 G有生成树 证明(充分性显然): 注意:若G是有简单回路的连通图,删除回路上的 一条边,G中的回路一定减少。(因此,用“破圈 法”总可以构造连通图的生成树) 简单无向图G是树 当且仅当 G有唯一的生成树。 注意:G中任一简单回路至少有三条不同的边
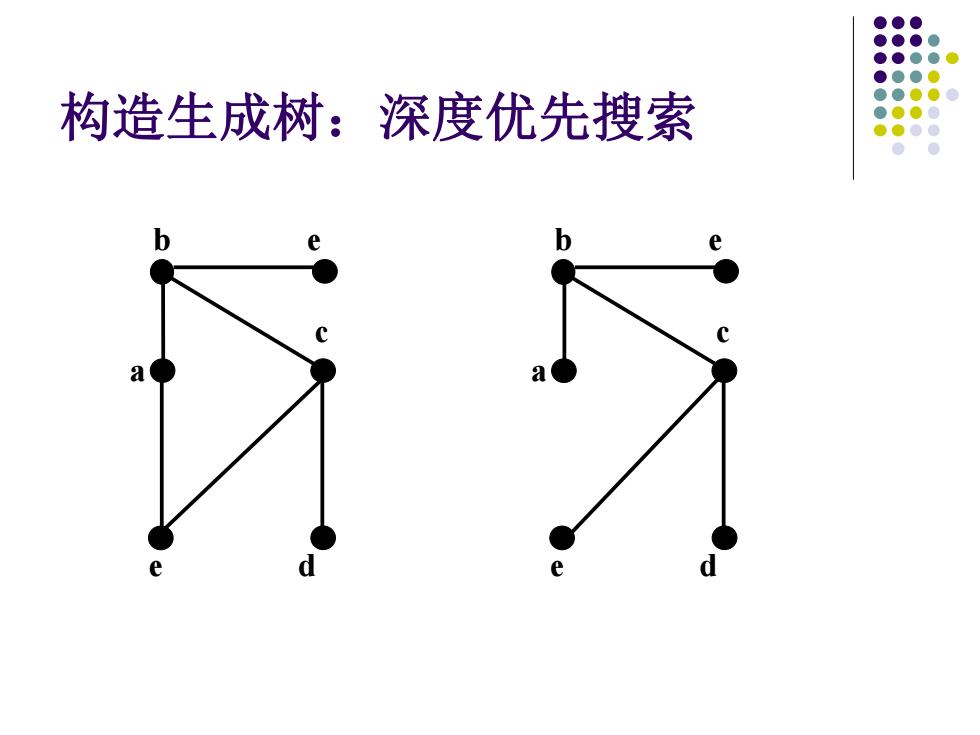
构造生成树:深度优先搜索
构造生成树:深度优先搜索 a c b e d e a c b e d e

深度优先搜索算法 Procedure DFS(G:带顶点1,,yn的连通图) T:=只包含顶点y的树; visit(v); Procedure visit(:G的]顶点) for每个邻居w{ ifw不在T中then{ 加入顶点w和边{y,w到T; visit(w);
深度优先搜索算法 Procedure DFS(G: 带顶点v1 , …,vn的连通图) T:=只包含顶点v1的树; visit(v1 ); Procedure visit(v: G的顶点) for v每个邻居w { if w不在T中 then { 加入顶点w和边{v, w}到T; visit(w); } }
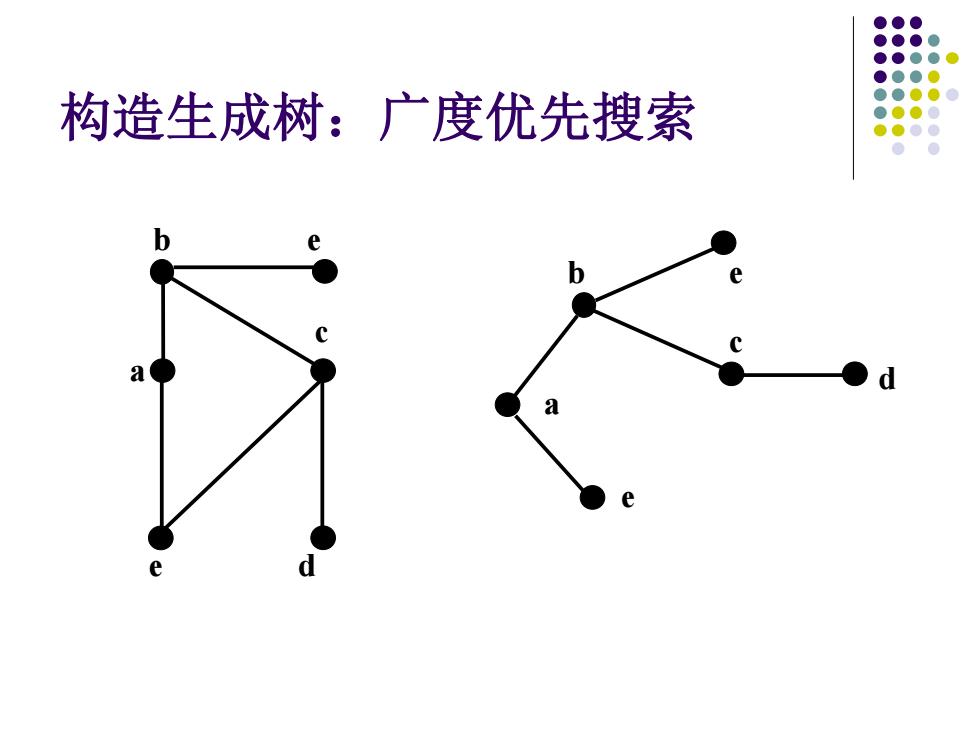
构造生成树:广度优先搜索
构造生成树:广度优先搜索 a b e d c e a c b e d e

广度优先搜索算法 Procedure BFS(G:带顶点y1,,yn的连通图) T:=只包含顶点y,的树;L:=空表;把y放入表L中 While L非空{ 删除L中的第一个顶点; for的每个邻居w{ ifw既不在L中也不在T中hen{ 加入w到L的末尾; 加入顶点w和边{y,w到T;
广度优先搜索算法 Procedure BFS(G: 带顶点v1 , …,vn的连通图) T:=只包含顶点v1的树; L:=空表; 把v1放入表L中 While L非空 { 删除L中的第一个顶点v; for v的每个邻居w { if w既不在L中也不在T中 then { 加入w到L的末尾; 加入顶点w和边{v, w}到T; } } }

Spanning Tree:Examples Different spanning tree are obtained from a symmetric, connected relatioin: Breadth first Breaking cycles Depth first
Spanning Tree: Examples Different spanning tree are obtained from a symmetric, connected relatioin: Breaking cycles Breadth first Depth first

最小生成树MST Minimum Spanning Tree ·考虑边有权重的连通无向图。其生成树可能不 唯一。定义生成树的权重为其所含各边之和。 一个带权连通图的最小生成树是其权重最小的 生成树。 ●注意,这里的最小(Minimum)并不意味着唯一。 。最小生成树有广泛的应用
最小生成树 MST Minimum Spanning Tree 考虑边有权重的连通无向图。其生成树可能不 唯一。定义生成树的权重为其所含各边之和。 一个带权连通图的最小生成树是其权重最小的 生成树。 注意,这里的最小(Minimum)并不意味着唯一。 最小生成树有广泛的应用

Prim算法(求最小生成树) 1:E={e,e是权最小的边 2:从E以外选择与E里顶点关联, 又不会与E中的边构成回路的 权最小的边加入E 3:重复第2步,直到E中包含n-1 条边 算法结束
Prim算法(求最小生成树) 1: E={e}, e是权最小的边 2: 从E以外选择与E里顶点关联, 又不会与E中的边构成回路的 权最小的边加入E 3: 重复第2步,直到E中包含n-1 条边 算法结束