
《概率论与数理统计I》 课程教学大纲 一、 课程基本信息 课程类型 理论课 课程编码 7029501 总学时48学时学分3学分 课程名称概率论与数理统计I 课程英文名称Probability and Mathematical Statistics I 适用专业 理工、经管等非统计专业 先修课程 (7030701)高等数学1、(7101201)线性代数1 开课部门理学院统计学系 二、 课程性质与目标 本课程为高等院校理工、经管等非统计专业四年制本科生的专业基础必修 课。为学生进一步学习相关专业课程奠定良好的概率统计基础,让学生熟悉概率 论与数理统计的基本概念,掌握处理随机现象的基本原理和方法,锻炼学生的逻 辑思维能力,培养学生运用所学知识分析和解决实际问题的能力。 课程目标1:学生应掌握概率论与数理统计的基本理论、基本思想和基本方 法。 课程目标2:学生应具备处理随机问题的基本意识和基本能力 课程目标3:学生应能利用所学的概率统计方法解决一些实际问题。 课程思政目标:根据概率论与数理统计课程处理随机数据的特点,运用课程 怡当案例进行点点滴滴、细致入微地培养社会主义建设的合格接班人。充分发挥 本课程所承载的育人功能,引导并积极优化学生的学习体验,实现较好的学习效 果。从而坚定学生理想信念、厚植爱国主义情怀、加强品德修养,进一步在培有 学生科学精神上下功夫,孕有学生的创新精神、工匠精神等为祖国建设和发展贡 献力量。 三、课程教学基本内容与要求 1.概率论的基础知识 基本内容:随机试验、随机事件、样本空间的概念:事件间的关系及事件的 运算:概率的统计定义、古典概型、概率的加法法则:条件概率、乘法公式、全 概率公式和贝叶斯公式:事件的独立性和几何概率。 1
1 《概率论与数理统计 I》 课程教学大纲 一、 课程基本信息 课程类型 理论课 课程编码 7029501 总学时 48 学时 学分 3 学分 课程名称 概率论与数理统计 I 课程英文名称 Probability and Mathematical Statistics I 适用专业 理工、经管等非统计专业 先修课程 (7030701)高等数学 I、(7101201)线性代数 I 开课部门 理学院统计学系 二、 课程性质与目标 本课程为高等院校理工、经管等非统计专业四年制本科生的专业基础必修 课。为学生进一步学习相关专业课程奠定良好的概率统计基础,让学生熟悉概率 论与数理统计的基本概念,掌握处理随机现象的基本原理和方法,锻炼学生的逻 辑思维能力,培养学生运用所学知识分析和解决实际问题的能力。 课程目标 1:学生应掌握概率论与数理统计的基本理论、基本思想和基本方 法。 课程目标 2: 学生应具备处理随机问题的基本意识和基本能力。 课程目标 3:学生应能利用所学的概率统计方法解决一些实际问题。 课程思政目标:根据概率论与数理统计课程处理随机数据的特点,运用课程 恰当案例进行点点滴滴、细致入微地培养社会主义建设的合格接班人。充分发挥 本课程所承载的育人功能,引导并积极优化学生的学习体验,实现较好的学习效 果。从而坚定学生理想信念、厚植爱国主义情怀、加强品德修养,进一步在培育 学生科学精神上下功夫,孕育学生的创新精神、工匠精神等为祖国建设和发展贡 献力量。 三、 课程教学基本内容与要求 1.概率论的基础知识 基本内容:随机试验、随机事件、样本空间的概念;事件间的关系及事件的 运算;概率的统计定义、古典概型、概率的加法法则;条件概率、乘法公式、全 概率公式和贝叶斯公式;事件的独立性和几何概率

要求: (①)理解随机事件和样本空间的概念,熟练掌握事件之间的关系和基本运算: (②)理解事件频率的概念,了解随机事件的统计规律性及概率的统计定义: (③)掌握概率的基本性质,并会用这些性质计算概率: (④)理解条件概率的概念,掌握乘法公式、全概率公式和贝叶斯公式,并会 应用这些公式: (⑤)掌握事件独立性的概念、贝努里试验概型及有关的概率计算 2.随机变量及其分布 基本内容:随机变量及其分布函数:离散型随机变量及其分布(0-1分布、 二项分布、超几何分布、泊松分布、几何分布):连续型随机变量及其分布(均 匀分布、指数分布及正态分布):随机变量函数的分布。 要求 ()了解随机变量的概念,掌握离散型和连续性随机变量的描述方法 (②)掌握随机变量的分布律、概率密度函数、分布函数的概念和性质及它们 之间的相互关系: (③)掌握二项分布、超几何分布、泊松分布、均匀分布和正态分布的性质和 特征: (④)会求简单的随机变量函数的分布。 3.多维随机变量及其分布 基本内容:二维随机变量;二维离散型随机变量:二维连续型随机变量:随 机变量的独立性:随机变量的函数的分布。 要求: ()掌握二维随机变量的联合分布、边缘分布、条件分布的概念及其相互关 系 (②)理解随机变量独立性的概念,并掌握其有关计算: (③)会求简单的二维随机变量函数的分布。 4.随机变量的数字特征 基本内容:随机变量的数学期望(定义、公式、性质):方差(定义、公式、 性质):协方差与相关系数:随机变量的矩。 要求: ()理解数学期望、方差的概念,并掌握它们的性质与计算,会计算随机变量 函数的数学期望: (②)掌握二项分布、泊松分布、超几何分布、几何分布、均匀分布、指数分 2
2 要求: ⑴ 理解随机事件和样本空间的概念,熟练掌握事件之间的关系和基本运算; ⑵ 理解事件频率的概念,了解随机事件的统计规律性及概率的统计定义; ⑶ 掌握概率的基本性质,并会用这些性质计算概率; ⑷ 理解条件概率的概念,掌握乘法公式、全概率公式和贝叶斯公式,并会 应用这些公式; ⑸ 掌握事件独立性的概念、贝努里试验概型及有关的概率计算。 2.随机变量及其分布 基本内容:随机变量及其分布函数;离散型随机变量及其分布(0-1 分布、 二项分布、超几何分布、泊松分布、几何分布);连续型随机变量及其分布(均 匀分布、指数分布及正态分布);随机变量函数的分布。 要求: ⑴ 了解随机变量的概念,掌握离散型和连续性随机变量的描述方法; ⑵ 掌握随机变量的分布律、概率密度函数、分布函数的概念和性质及它们 之间的相互关系; ⑶ 掌握二项分布、超几何分布、泊松分布、均匀分布和正态分布的性质和 特征; ⑷ 会求简单的随机变量函数的分布。 3.多维随机变量及其分布 基本内容:二维随机变量;二维离散型随机变量;二维连续型随机变量;随 机变量的独立性;随机变量的函数的分布。 要求: ⑴ 掌握二维随机变量的联合分布、边缘分布、条件分布的概念及其相互关 系; ⑵ 理解随机变量独立性的概念,并掌握其有关计算; ⑶ 会求简单的二维随机变量函数的分布。 4.随机变量的数字特征 基本内容:随机变量的数学期望(定义、公式、性质);方差(定义、公式、 性质);协方差与相关系数;随机变量的矩。 要求: ⑴ 理解数学期望、方差的概念,并掌握它们的性质与计算,会计算随机变量 函数的数学期望; ⑵ 掌握二项分布、泊松分布、超几何分布、几何分布、均匀分布、指数分

布及正态分布的数学期望和方差; ③)了解协方差及相关系数的概念、性质与计算 (④)了解矩的概念。 5.大数定律及中心极限定理 基本内容:大数定律(定义、引理:契比雪夫大数定律、伯努利大数定律、 辛软大数定律)、中心极限定理(林德伯格一勒维中心极限定理、李雅普诺夫中 心极限定理、德莫佛一拉普拉斯中心极限定理), 要求: ()掌握契比雪夫不等式: (②)了解契比雪夫、贝努利和辛钦大数定理: (3)理解独立同分布的中心极限定理及德莫佛一拉普拉斯定理,了解李雅普 诺夫中心极限定理 6.样本及抽样分布 基本内容:简单随机样本及相关概念:统计量及其相关概念:抽样分布(x 分布、1分布、F布)的概念、性质和正态总体的抽样分布及相关定理。 要求: (①)理解总体、样本、统计量和抽样分布的概念: (②)掌握样本均值、样本方差和样本矩的计算: (③)了解x分布、:分布、F分布的定义和特征,并会查相应的分位数表: (④了解正态分布的某些常用统计量的分布。 7.参数估计 基本内容:点估计(矩估计法、最大似然估计法)的定义、原理及求法步骤: 估计量的评价标准:区间估计(正态总体均值的区间估计、均值差的区间估计 方差与方差比的区间估计)。 要求: ()理解点估计的概念,掌握矩估计法和极大似然估计法: (②)了解估计量的评价标准: ()理解区间估计的概念,会求正态总体的均值与方差的置信区间。 8.假设检验 基本内容:假设检验的基本概念、单个正态总体参数的假设检验、两个正态 总体参数的假设检验。 要求: ()理解假设检验的基本思想,掌握假设检验的基本步骤及两类错误:
3 布及正态分布的数学期望和方差; ⑶ 了解协方差及相关系数的概念、性质与计算; ⑷ 了解矩的概念。 5.大数定律及中心极限定理 基本内容:大数定律(定义、引理;契比雪夫大数定律、伯努利大数定律、 辛钦大数定律)、中心极限定理(林德伯格—勒维中心极限定理、李雅普诺夫中 心极限定理、德莫佛—拉普拉斯中心极限定理)。 要求: ⑴ 掌握契比雪夫不等式; ⑵ 了解契比雪夫、贝努利和辛钦大数定理; ⑶ 理解独立同分布的中心极限定理及德莫佛—拉普拉斯定理,了解李雅普 诺夫中心极限定理。 6.样本及抽样分布 基本内容:简单随机样本及相关概念;统计量及其相关概念;抽样分布( 2 分布、t 分布、 F 布)的概念、性质和正态总体的抽样分布及相关定理。 要求: ⑴ 理解总体、样本、统计量和抽样分布的概念; ⑵ 掌握样本均值、样本方差和样本矩的计算; ⑶ 了解 2 分布、t 分布、 F 分布的定义和特征,并会查相应的分位数表; ⑷ 了解正态分布的某些常用统计量的分布。 7.参数估计 基本内容:点估计(矩估计法、最大似然估计法)的定义、原理及求法步骤; 估计量的评价标准;区间估计(正态总体均值的区间估计、均值差的区间估计、 方差与方差比的区间估计)。 要求: ⑴ 理解点估计的概念,掌握矩估计法和极大似然估计法; ⑵ 了解估计量的评价标准; ⑶ 理解区间估计的概念,会求正态总体的均值与方差的置信区间。 8.假设检验 基本内容:假设检验的基本概念、单个正态总体参数的假设检验、两个正态 总体参数的假设检验。 要求: ⑴ 理解假设检验的基本思想,掌握假设检验的基本步骤及两类错误;
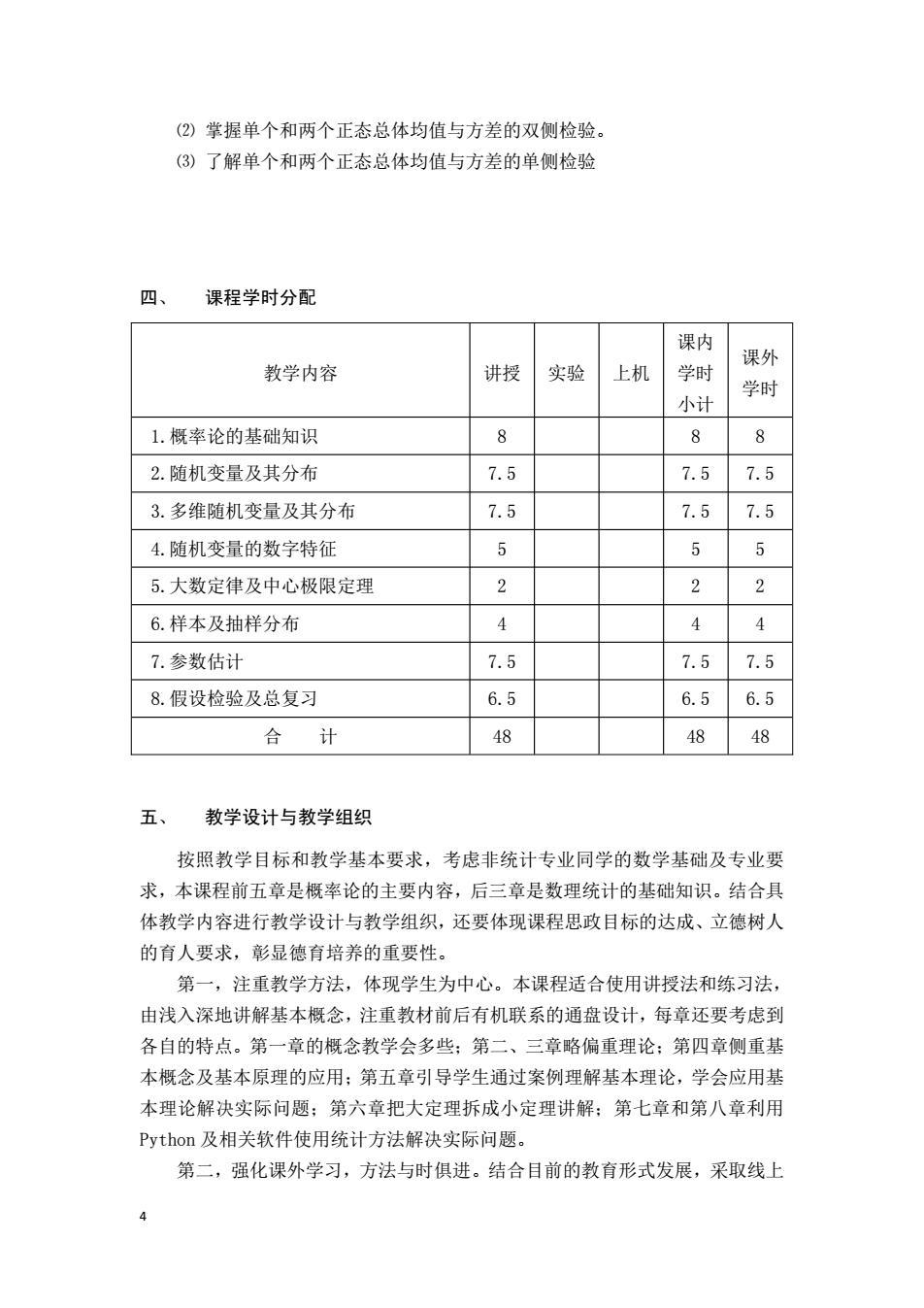
(②)掌握单个和两个正态总体均值与方差的双侧检验。 (③)了解单个和两个正态总体均值与方差的单侧检验 四、 课程学时分配 课内 课外 教学内容 讲授 实验 上机 学时 学时 小计 1.概率论的基础知识 8 2.随机变量及其分布 7.5 7.5 7.5 3.多维随机变量及其分布 7.5 7.5 7.5 4.随机变量的数字特征 5 5.大数定律及中心极限定理 2 6.样本及抽样分布 4 7.参数估计 7.5 7.5 7.5 8.假设检验及总复习 6.5 6.5 6.5 合计 48 48 48 五、 教学设计与教学组织 按照教学目标和教学基本要求,考虑非统计专业同学的数学基础及专业要 求,本课程前五章是概率论的主要内容,后三章是数理统计的基础知识。结合具 体教学内容进行教学设计与教学组织,还要体现课程思政目标的达成、立德树人 的育人要求,彰显德育培养的重要性。 第一,注重教学方法,体现学生为中心。本课程适合使用讲授法和练习法, 由浅入深地讲解基本概念,注重教材前后有机联系的通盘设计,每章还要考虑到 各自的特点。第一章的概念教学会多些:第二、三章略偏重理论:第四章侧重基 本概念及基本原理的应用:第五章引导学生通过案例理解基本理论,学会应用基 本理论解决实际问题:第六章把大定理拆成小定理讲解:第七章和第八章利用 Python及相关软件使用统计方法解决实际问题。 第二,强化课外学习,方法与时俱进。结合目前的教育形式发展,采取线上 4
4 ⑵ 掌握单个和两个正态总体均值与方差的双侧检验。 ⑶ 了解单个和两个正态总体均值与方差的单侧检验 四、 课程学时分配 教学内容 讲授 实验 上机 课内 学时 小计 课外 学时 1.概率论的基础知识 8 8 8 2.随机变量及其分布 7.5 7.5 7.5 3.多维随机变量及其分布 7.5 7.5 7.5 4.随机变量的数字特征 5 5 5 5.大数定律及中心极限定理 2 2 2 6.样本及抽样分布 4 4 4 7.参数估计 7.5 7.5 7.5 8.假设检验及总复习 6.5 6.5 6.5 合 计 48 48 48 五、 教学设计与教学组织 按照教学目标和教学基本要求,考虑非统计专业同学的数学基础及专业要 求,本课程前五章是概率论的主要内容,后三章是数理统计的基础知识。结合具 体教学内容进行教学设计与教学组织,还要体现课程思政目标的达成、立德树人 的育人要求,彰显德育培养的重要性。 第一,注重教学方法,体现学生为中心。本课程适合使用讲授法和练习法, 由浅入深地讲解基本概念,注重教材前后有机联系的通盘设计,每章还要考虑到 各自的特点。第一章的概念教学会多些;第二、三章略偏重理论;第四章侧重基 本概念及基本原理的应用;第五章引导学生通过案例理解基本理论,学会应用基 本理论解决实际问题;第六章把大定理拆成小定理讲解;第七章和第八章利用 Python 及相关软件使用统计方法解决实际问题。 第二,强化课外学习,方法与时俱进。结合目前的教育形式发展,采取线上

线下结合,课前利用雨课堂、企业微信课程群、MOOC及往届的录像形成系统的 课外练习资料,并设计课堂与学生互动细节,调动、激励学生主动性与创造性 体现学生为中心,实现工程教育的培养目标,体现工程教育专业认证理念之“结 果导向”。 第三,注重过程考核,严保学习质量。综合考虑教学内容与要求、学生基础、 课程性质与目标等因素,充分利用现代信息技术等教学手段,比如雨课堂实现与 所有学生的课堂上随机互动,随时展示学生的学习成果。精心设计课后作业,注 意问题的典型性与代表性并且难易结合,通过作业检查学生对概念的理解对理论 的运用,有利于对学生学习成果的科学评价。 第四,精心组织教学。围绕基本知识基本理论及学生的基本情况,及工程教 育专业认证目标进行教学组织,充分体现现代教学方法、手段,全面体现线上线 下混合教学的优点和长处,认真组织教学,在大的教学班中尽量关照调动每个同 学的学习情况,巧妙设计课堂线上训练题,使学生的通讯工具变成有利于学习的 工具。 第五,科学评价教学。好的教学设计和教学组织要体现合适的学生学法和教 师教法,选用科学恰当的评估方式非常重要。本课程重复利用大数据技术对学生 的每一点反馈、练习结果都进行量化评估,科学评估教法和学法,本课程平时成 绩占40%,期末考试占60%,平时成绩涵盖学习过程的方方面面并进行适当的加 权,权重会根据实际情况进行调整。 第六,三全育人融入教学。第一章概率论的基础知识中,引入中奖问题、新 冠感染率、“狼来了”等具体例子,培有学生的爱国主义精神和学习热情,教育 学生要诚实守信:第二、三章的讲解过程中,引入工程中常见的各种分布,如通 过二项分布在生产维修中的应用,培育学生团结合作意识:第四章的学习,利用 数学期望和方差来求解证券投资组合问题:第五章应用到通信理论、信号处理中 的除噪问题,培养科学精神:第六章引导学生思考概率与统计的关系,建立知识 体系意识:第七章、八章强调点估计和假设检验在工业生产中的应用,培养学生 解决实际问题的能力。 总之,教学方式和教学组织要结合概率论与数理统计的课程特点,围绕工程 教育的结果导向,充分利用现代教育技术,科学恰当地进行教学设计、体现学生 为中心,精心进行教学组织,全面调动学生学习积极性,掌握科学知识并服务于 社会发展。 六、教材与参考资料 1.教材 《概率论与数理统计》(第1版),刘喜波等主编,北京:北京邮电大学出版
5 线下结合,课前利用雨课堂、企业微信课程群、MOOC 及往届的录像形成系统的 课外练习资料,并设计课堂与学生互动细节,调动、激励学生主动性与创造性, 体现学生为中心,实现工程教育的培养目标,体现工程教育专业认证理念之“结 果导向”。 第三,注重过程考核,严保学习质量。综合考虑教学内容与要求、学生基础、 课程性质与目标等因素,充分利用现代信息技术等教学手段,比如雨课堂实现与 所有学生的课堂上随机互动,随时展示学生的学习成果。精心设计课后作业,注 意问题的典型性与代表性并且难易结合,通过作业检查学生对概念的理解对理论 的运用,有利于对学生学习成果的科学评价。 第四,精心组织教学。围绕基本知识基本理论及学生的基本情况,及工程教 育专业认证目标进行教学组织,充分体现现代教学方法、手段,全面体现线上线 下混合教学的优点和长处,认真组织教学,在大的教学班中尽量关照调动每个同 学的学习情况,巧妙设计课堂线上训练题,使学生的通讯工具变成有利于学习的 工具。 第五,科学评价教学。好的教学设计和教学组织要体现合适的学生学法和教 师教法,选用科学恰当的评估方式非常重要。本课程重复利用大数据技术对学生 的每一点反馈、练习结果都进行量化评估,科学评估教法和学法,本课程平时成 绩占 40%,期末考试占 60%,平时成绩涵盖学习过程的方方面面并进行适当的加 权,权重会根据实际情况进行调整。 第六,三全育人融入教学。第一章概率论的基础知识中,引入中奖问题、新 冠感染率、“狼来了”等具体例子,培育学生的爱国主义精神和学习热情,教育 学生要诚实守信;第二、三章的讲解过程中,引入工程中常见的各种分布,如通 过二项分布在生产维修中的应用,培育学生团结合作意识;第四章的学习,利用 数学期望和方差来求解证券投资组合问题;第五章应用到通信理论、信号处理中 的除噪问题,培养科学精神;第六章引导学生思考概率与统计的关系,建立知识 体系意识;第七章、八章强调点估计和假设检验在工业生产中的应用,培养学生 解决实际问题的能力。 总之,教学方式和教学组织要结合概率论与数理统计的课程特点,围绕工程 教育的结果导向,充分利用现代教育技术,科学恰当地进行教学设计、体现学生 为中心,精心进行教学组织,全面调动学生学习积极性,掌握科学知识并服务于 社会发展。 六、 教材与参考资料 1.教材 《概率论与数理统计》(第 1 版),刘喜波等主编,北京:北京邮电大学出版

社出版,2020.8,ISBN:978756356003 2.参考资料 《概率论与数理统计》(第4版),盛骤等主编,北京:北京高等教育出版社 出版,2008.6,ISBN:9787040238969 七、课程考核方式与成绩评定标准 本课程期末采用闭卷考试形式,期末考试成绩占学期总成绩的60%,平时成 绩占学期总成绩的40%。平时成绩包括每次课后作业、课堂提问、平时练习(线 上考核、线下小测等)、考勤等。 八、大纲制(修)订说明 无 大纲执笔人:崔玉杰 大纲审核人:徐嗣棪 开课系主任:刘喜波 开课学院教学副院长:李红梅 制(修)订日期:2021年8月 6
6 社出版,2020.8,ISBN:9787563560035 2.参考资料 《概率论与数理统计》(第 4 版),盛骤等主编,北京:北京高等教育出版社 出版,2008.6,ISBN:9787040238969 七、 课程考核方式与成绩评定标准 本课程期末采用闭卷考试形式,期末考试成绩占学期总成绩的 60%,平时成 绩占学期总成绩的 40%。平时成绩包括每次课后作业、课堂提问、平时练习(线 上考核、线下小测等)、考勤等。 八、 大纲制(修)订说明 无 大纲执笔人:崔玉杰 大纲审核人:徐嗣棪 开课系主任:刘喜波 开课学院教学副院长:李红梅 制(修)订日期:2021 年 8 月