
《复变函数与积分变换》 课程教学大纲 课程基本信息 总学时为学时数 ☑理论课(含上机、实验学时) 课程类型 总学时为周数 口实习 口课程设计口毕业设计 课程编码 7029401 总学时48 学分 3 课程名称 复变函数与积分变换 课程英文名称Complex Variable Function and Integral Transformation 适用专业 工科专业 先修课程 (7030702)高等数学 开课部门 理学院数学系 二、 课程性质与目标 《复变函数与积分变换》是工科专业一门主要的专业必修课,是高等数学的 后续课程。它的理论和方法,对于数学的其他学科,对于物理、力学、工程技术 中的一些问题,有许多重要的应用。通过本课程的教学,学生为从事教学、科研 及其他实际工作打好基础。 课程目标1:学生应掌握复变函数与积分变换的基本理论和方法。 课程目标2:学生应能获得独立地分析和解决某些实际问题的能力。 课程思政目标:数学学科发现发展的历史,培养学生感受人类对真理的不断 追求,对未知世界的强烈好奇心和求知欲,激发学生的科学精神与创新精神:教 学过程中培养学生抓住问题本质的意识、能力以及严谨务实的科学态度:面对复 杂问题的分析,培养学生看问题看大势、看主流的大局观和判断力,激发责任心 和使命感。培育学生科学精神、创新精神、工匠精神等。 三、 课程教学基本内容与要求 1.复数与复变函数 基本内容及要求: (1)掌握复数的各种表示方法及其运算。 (2)了解区域的概念。 (3)理解复变函数的概念。 (4)学握复变函数的极限和连续的概念
《复变函数与积分变换》 课程教学大纲 一、 课程基本信息 课程类型 总学时为学时数 理论课(含上机、实验学时) 总学时为周数 □实习 □课程设计 □毕业设计 课程编码 7029401 总学时 48 学分 3 课程名称 复变函数与积分变换 课程英文名称 Complex Variable Function and Integral Transformation 适用专业 工科专业 先修课程 (7030702)高等数学 开课部门 理学院数学系 二、 课程性质与目标 《复变函数与积分变换》是工科专业一门主要的专业必修课,是高等数学的 后续课程。它的理论和方法,对于数学的其他学科,对于物理、力学、工程技术 中的一些问题,有许多重要的应用。通过本课程的教学,学生为从事教学、科研 及其他实际工作打好基础。 课程目标 1:学生应掌握复变函数与积分变换的基本理论和方法。 课程目标 2:学生应能获得独立地分析和解决某些实际问题的能力。 课程思政目标:数学学科发现发展的历史,培养学生感受人类对真理的不断 追求,对未知世界的强烈好奇心和求知欲,激发学生的科学精神与创新精神;教 学过程中培养学生抓住问题本质的意识、能力以及严谨务实的科学态度;面对复 杂问题的分析,培养学生看问题看大势、看主流的大局观和判断力,激发责任心 和使命感。培育学生科学精神、创新精神、工匠精神等。 三、 课程教学基本内容与要求 1.复数与复变函数 基本内容及要求: (1)掌握复数的各种表示方法及其运算。 (2)了解区域的概念。 (3)理解复变函数的概念。 (4)掌握复变函数的极限和连续的概念

(5)理解复变函数的导数及解析函数的概念。 (6)掌握复变函数解析的充要条件。 (7)了解常见初等解析函数 重点:复变函数的概念,解析函数的基本概念。 难点:解析函数的概念。 2.复变函数的积分 基本内容及要求: (1)理解复变函数积分的定义,了解其性质,会求复变函数的积分 (2)熟练学握Cauchy-Courcas定理、复合闭路定理、柯西积分公式。 (3)了解Cauchy-Courcas定理、复合闭路定理、柯西积分公式的证明。 (4)会求解析函数的高阶导数。 (5)掌握解析函数与调和函数基本概念。 重点:Cauchy-Courcas定理,复合闭路定理,柯西积分公式。 难点:Cauchy--Courcas定理,复合闭路定理,柯西积分公式。 3.级数 基本内容及要求: (1)理解复数项级数收敛、发散及绝对收敛等概念。 (2)了解幂级数收敛圆的概念,掌握收敛半径的求法,了解收敛圆内的一 些基本性质。 (3)了解泰勒定理,会e、sin:、Ln0+)、(+的麦克劳林展开式,并 能利用它们将一些简单的解析函数展开为幂级数。 (4)了解罗朗定理,掌握将简单的函数展开为罗朗级数的间接方法。 重点:收敛半径的求法,解析函数展开为幂级数的方法,简单的函数展 开为罗朗级数的间接方法。 难点:解析函数展开为幂级数的方法,简单的函数展开为罗朗级数的间 接方法。 4.留数理论及其应用 基本内容及要求: (1)掌握极点处留数的求法以及用留数求复变函数沿闭路积分的方法。 (2)掌握孤立奇点的分类与性质。 (3)了解孤立奇点性质的证明。 (4)掌握留数的概念和留数计算定积分的方法。 重点:极点处留数的求法,用留数求复变函数沿闭路积分的方法,留数 计算定积分的方法
(5)理解复变函数的导数及解析函数的概念。 (6)掌握复变函数解析的充要条件。 (7)了解常见初等解析函数。 重 点:复变函数的概念,解析函数的基本概念。 难 点:解析函数的概念。 2. 复变函数的积分 基本内容及要求: (1)理解复变函数积分的定义,了解其性质,会求复变函数的积分。 (2)熟练掌握 Cauchy-Courcas 定理、复合闭路定理、柯西积分公式。 (3)了解 Cauchy-Courcas 定理、复合闭路定理、柯西积分公式的证明。 (4)会求解析函数的高阶导数。 (5)掌握解析函数与调和函数基本概念。 重 点:Cauchy-Courcas 定理, 复合闭路定理,柯西积分公式。 难 点:Cauchy-Courcas 定理, 复合闭路定理,柯西积分公式。 3. 级数 基本内容及要求: (1)理解复数项级数收敛、发散及绝对收敛等概念。 (2)了解幂级数收敛圆的概念,掌握收敛半径的求法,了解收敛圆内的一 些基本性质。 (3)了解泰勒定理,会 z e 、sin z 、Ln 1 z 、1 z 的麦克劳林展开式,并 能利用它们将一些简单的解析函数展开为幂级数。 (4)了解罗朗定理,掌握将简单的函数展开为罗朗级数的间接方法。 重 点:收敛半径的求法,解析函数展开为幂级数的方法,简单的函数展 开为罗朗级数的间接方法。 难 点:解析函数展开为幂级数的方法,简单的函数展开为罗朗级数的间 接方法。 4. 留数理论及其应用 基本内容及要求: (1)掌握极点处留数的求法以及用留数求复变函数沿闭路积分的方法。 (2)掌握孤立奇点的分类与性质。 (3)了解孤立奇点性质的证明。 (4)掌握留数的概念和留数计算定积分的方法。 重 点:极点处留数的求法,用留数求复变函数沿闭路积分的方法,留数 计算定积分的方法
难点:用留数求复变函数沿闭路积分的方法,留数计算定积分的方法。 5.傅氏变换 基本内容及要求: (1)了解傅氏积分的概念及傅氏积分定理。 (2)了解8函数及其傅氏变换,了解频谱的概念,掌握求傅氏变换和傅氏 逆变换的方法,会计算简单的问题。 (3)掌握傅氏变换的性质并能用于计算,了解查表方法, (4)了解卷积的概念及卷积定理,掌握卷积的计算方法。 重点:求傅氏变换和傅氏逆变换的方法,卷积的计算方法。 雅点:求傅氏变换和傅氏逆变换的方法。 6.拉氏变换 基本内容及要求: (1)了解拉氏变换的概念及拉氏变换存在定理。掌握求拉氏变换的方法, 会解一般的问题。 (2)掌握拉氏变换的性质并能用于计算,了解查表方法。 (3)了解拉氏逆变换的概念,掌握求拉氏逆变换的方法。 (4)了解卷积的概念及卷积定理,掌握卷积的计算方法。 (5)掌握用拉氏变换求解微分方程或微分方程组的方法。 重点:求拉氏变换的方法,求拉氏逆变换的方法。 难点:求拉氏变换的方法,求拉氏逆变换的方法。 四、 课程学时分配 课内 课外 教学内容 讲授 实验 习题 学时 学时 小计 1.复数与复变函数 10 2.复变函数的积分 8 3.级数 6 4.留数理论及其应用 6 2 5.傅氏变换 4 6.拉氏变换 合 、计 10 48 五、 实践性教学内容的安排与要求
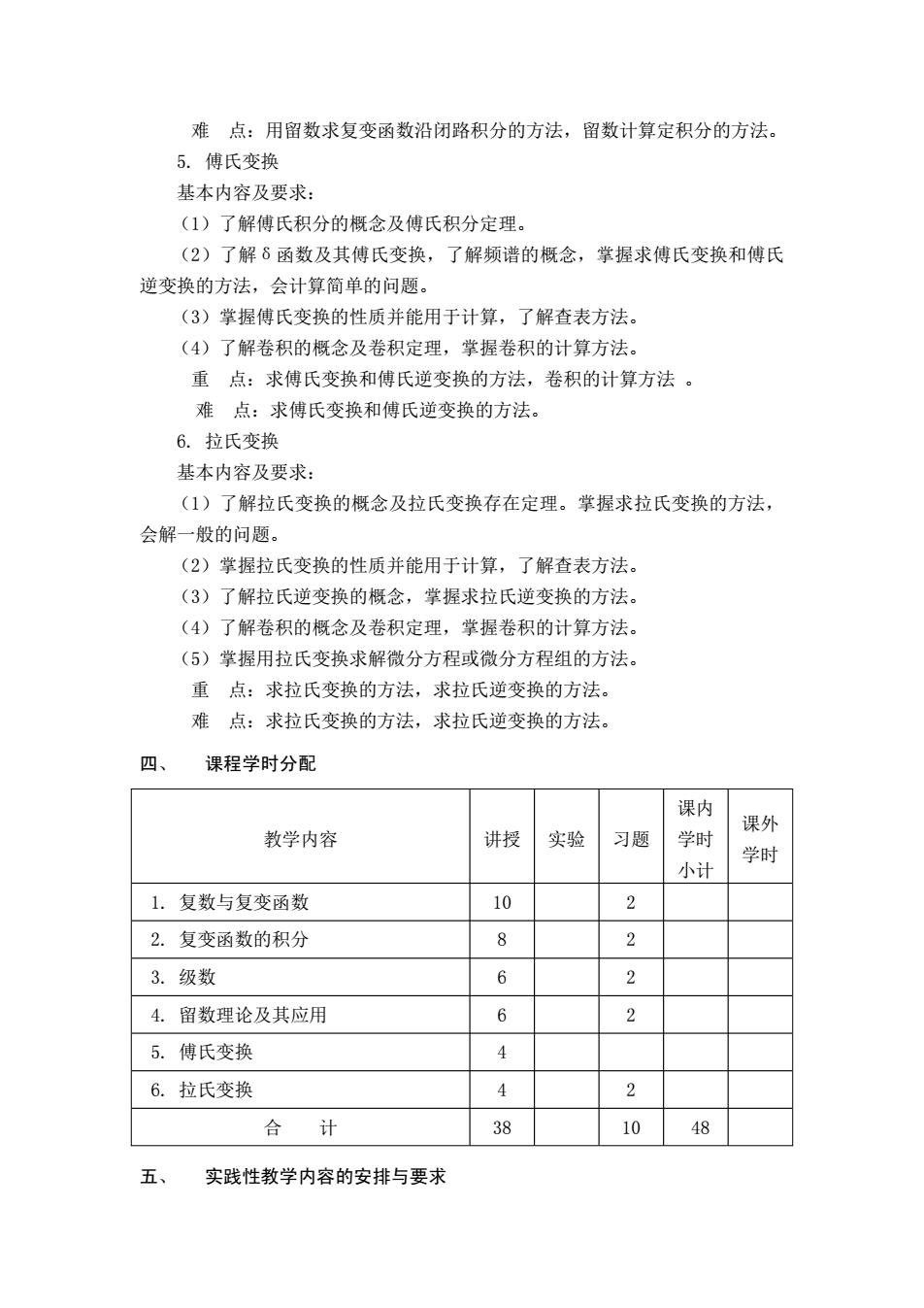
难 点:用留数求复变函数沿闭路积分的方法,留数计算定积分的方法。 5. 傅氏变换 基本内容及要求: (1)了解傅氏积分的概念及傅氏积分定理。 (2)了解δ函数及其傅氏变换,了解频谱的概念,掌握求傅氏变换和傅氏 逆变换的方法,会计算简单的问题。 (3)掌握傅氏变换的性质并能用于计算,了解查表方法。 (4)了解卷积的概念及卷积定理,掌握卷积的计算方法。 重 点:求傅氏变换和傅氏逆变换的方法,卷积的计算方法 。 难 点:求傅氏变换和傅氏逆变换的方法。 6. 拉氏变换 基本内容及要求: (1)了解拉氏变换的概念及拉氏变换存在定理。掌握求拉氏变换的方法, 会解一般的问题。 (2)掌握拉氏变换的性质并能用于计算,了解查表方法。 (3)了解拉氏逆变换的概念,掌握求拉氏逆变换的方法。 (4)了解卷积的概念及卷积定理,掌握卷积的计算方法。 (5)掌握用拉氏变换求解微分方程或微分方程组的方法。 重 点:求拉氏变换的方法,求拉氏逆变换的方法。 难 点:求拉氏变换的方法,求拉氏逆变换的方法。 四、 课程学时分配 教学内容 讲授 实验 习题 课内 学时 小计 课外 学时 1. 复数与复变函数 10 2 2. 复变函数的积分 8 2 3. 级数 6 2 4. 留数理论及其应用 6 2 5. 傅氏变换 4 6. 拉氏变换 4 2 合 计 38 10 48 五、 实践性教学内容的安排与要求

为保证达到本课程的教学目的和教学要求,必须布置适量的课外作业,原则 上可安排18小时的课外作业 六、 教学设计与教学组织 教学设计:本课程属基础理论课,思想性强,教学内容与相关基础课及专业 课程联系较多。教师在教学中应充分利用如PPT、网络视频等现代信息技术:教 师应注重启发并引导学生学握重要概念的背景思想,理解重要概念的思想本质, 培养学生应用数学思想方法解决应用问题的能力。同时,通过对数学思想和理论 的建立和推演过 达到激发 老生好奇心和求知欲、培养科 与创新精科 育人要求。教学环节包括理论教学、课堂练习、课后作业、答疑及辅导等。教 在教学中注重过程培养,一方面通过教法加深学生对课堂教学内容的理解和对理 论知识的掌握,提高学生分析问题和解决问题能力:另一方面,教学中适当地介 绍本课程和专业课程之间的关系,促进学生学习本课程的主动性和积极性。 教学组织:基于本学科课堂信息量、难度高等特点,课堂教学应以教师讲授 为主,并辅 课堂练 习、课后作业和 习题讲解。教师做到作业全批全 攻。 学生应 按时保质保量地完成作业,特别强化课后作业和答疑辅导环节。通过目标达成, 本课程将调动学生的学习兴趣,增强学生解决问题的能力。 七、教材与参考资料 1.教材 《复变函数与积分变换》,张建国、李冱岸主编,机械工业出版社出版,2013 年6月,ISBN:9787111645375 2.参考资料 (1)《复变函数与积分变换》,杨巧林主编,机械工业出版社出版,2012年 12月,ISBN:9787111430841 (2)《复变函数与积分变换》,焦红伟、尹景本主编,北京大学出版社出版 2007年9月,1SBN:9787301126349 八、课程考核方式与成绩评定标准 定期考试和平时作业双向考查。采用闭卷笔试,要求卷面内容覆盖本大纲 80%以上。以百分制评定成绩,平时成绩占30%,期末成绩占70%。平时成绩由作 业成绩、考勤两部分组成,其中作业占90%,考勤占10%。 九、大纲制(修)订说明 无 大纲执笔人:孔新雷
为保证达到本课程的教学目的和教学要求,必须布置适量的课外作业,原则 上可安排 18 小时的课外作业。 六、 教学设计与教学组织 教学设计:本课程属基础理论课,思想性强,教学内容与相关基础课及专业 课程联系较多。教师在教学中应充分利用如 PPT、网络视频等现代信息技术;教 师应注重启发并引导学生掌握重要概念的背景思想,理解重要概念的思想本质, 培养学生应用数学思想方法解决应用问题的能力。同时,通过对数学思想和理论 的建立和推演过程,达到激发学生好奇心和求知欲、培养科学精神与创新精神的 育人要求。教学环节包括理论教学、课堂练习、课后作业、答疑及辅导等。教师 在教学中注重过程培养,一方面通过教法加深学生对课堂教学内容的理解和对理 论知识的掌握,提高学生分析问题和解决问题能力;另一方面,教学中适当地介 绍本课程和专业课程之间的关系,促进学生学习本课程的主动性和积极性。 教学组织:基于本学科课堂信息量、难度高等特点,课堂教学应以教师讲授 为主,并辅以课堂练习、课后作业和习题讲解。教师做到作业全批全改。学生应 按时保质保量地完成作业,特别强化课后作业和答疑辅导环节。通过目标达成, 本课程将调动学生的学习兴趣,增强学生解决问题的能力。 七、 教材与参考资料 1.教材 《复变函数与积分变换》,张建国、李冱岸主编,机械工业出版社出版,2013 年 6 月,ISBN:9787111645375 2.参考资料 (1)《复变函数与积分变换》,杨巧林主编,机械工业出版社出版,2012 年 12 月,ISBN:9787111430841 (2)《复变函数与积分变换》,焦红伟、尹景本主编,北京大学出版社出版, 2007 年 9 月,ISBN:9787301126349 八、 课程考核方式与成绩评定标准 定期考试和平时作业双向考查。采用闭卷笔试,要求卷面内容覆盖本大纲 80%以上。以百分制评定成绩,平时成绩占 30%,期末成绩占 70%。平时成绩由作 业成绩、考勤两部分组成,其中作业占 90%,考勤占 10%。 九、 大纲制(修)订说明 无 大纲执笔人:孔新雷

大纲审核人:孙明正 开课系主任:邹杰涛 开课学院教学副院长:李红梅 制(修)订日期:2021年08月
大纲审核人:孙明正 开课系主任:邹杰涛 开课学院教学副院长:李红梅 制(修)订日期:2021 年 08 月