
《高等数学B1》课程教学大纲(0BE模式) 一、课程基本信息 1.课程名称 高等数学B1 Advanced Mathematics B1 2.课程代码 13208013 3.课程类别 数理基础课程 4.课程性质 必修 5.学时/学分 64/4 6.先修课程 初等数学 7.后续课程 高等数学B2、概率论与数理统计、统计学等 8.适用专业 国际贸易、财务管理、市场营销、会计、旅游、金融、公共事业管理等各经济本科专业 二、课程的主要任务及目标 1.课程的主要任务 《高等数学B1》课程是高等学校经济管理各专业必修的一门重要基础理论课。通过本 课程的学习,一方面要使学生掌握高等数学B1的基本概念、基本理论和基本运算技能, 为学习后继课程和进一步获得数学知识奠定必要的数学基础。另一方面通过本课程的学 习,逐步培养学生具有比较熟练的运算能力,一定的抽象思维能力和逻辑推理能力以及运 用所学知识去分析、解决各类经济活动中的实际问题的能力,准确理解和勇于创新的能力, 提高学生的素质。在讲授该门课程时,应结合应用型大学数学课程的特点和思政教育的内 涵,通过学习数学定义、公式、定理,理解数学思想,使学生对事物的方法规律有本质的 认识,培养学生的辩证唯物主义观。在立足知识的前提下,借助数学发展史、典故以及优 秀的数学家奋斗历程等,培养学生不畏艰难、坚持到底的科学态度和创新精神,同时引导 1
1 《高等数学 B1》课程教学大纲(OBE 模式) 一、课程基本信息 1.课程名称 高等数学 B1 / Advanced Mathematics B1 2.课程代码 13208013 3.课程类别 数理基础课程 4.课程性质 必修 5.学时/学分 64/4 6.先修课程 初等数学 7. 后续课程 高等数学 B2、概率论与数理统计、统计学等 8.适用专业 国际贸易、财务管理 、市场营销、会计、旅游、金融、公共事业管理等各经济本科专业 二、课程的主要任务及目标 1.课程的主要任务 《高等数学 B1》课程是高等学校经济管理各专业必修的一门重要基础理论课。通过本 课程的学习,一方面要使学生掌握高等数学 B1 的基本概念、基本理论和基本运算技能, 为学习后继课程和进一步获得数学知识奠定必要的数学基础。另一方面通过本课程的学 习,逐步培养学生具有比较熟练的运算能力,一定的抽象思维能力和逻辑推理能力以及运 用所学知识去分析、解决各类经济活动中的实际问题的能力,准确理解和勇于创新的能力, 提高学生的素质。在讲授该门课程时,应结合应用型大学数学课程的特点和思政教育的内 涵,通过学习数学定义、公式、定理,理解数学思想,使学生对事物的方法规律有本质的 认识,培养学生的辩证唯物主义观。在立足知识的前提下,借助数学发展史、典故以及优 秀的数学家奋斗历程等,培养学生不畏艰难、坚持到底的科学态度和创新精神,同时引导

学生学会有效沟通交流,增强其团队合作意识,提高学生的实践能力、创造能力、就业能 力和创业能力。 2.课程目标 根据课程的主要任务,现确定高等数学B1课程目标如下: 课程目标1:掌握经济管理中有关问题所需的微积分相关基础理论知识。 熟练学握微积分的相关基础理论知识,培养学生对相关数学概念、定理及一些结论的 理解能力和逻辑推理能力。 课程目标2:提升在经济管理等各方面解决相关问题所需的计算能力及应用能力。 熟练掌握微积分中遇到的各种计算问题的计算方法,并能够以此为工具分析和处理经 济管理中的实际问题。通过计算结果,能准确地分析其在经济管理中的意义。 三、课程教学内容与学时分配 支 推 知识单 知识点 敏学基本要求 学 号元/童节 学 时 式 标 1、了解函数的四个基本性质- -单调性、有界性、奇偶性和层 第二方:集合与函数 期性。 2、理解反函数、复合函数、分 讲 第一章 复合函数概念,初等函数概念 函数的概念 理解常见的经济 授 4 函数 第二节:经济学中的常用函数 讨1、2 知识点:五类常见的经济函数一需求函数 3、掌界复合函数的复合过程以及 论 供给函数、成本函数、收入函数、利润函数。 基本初等函数的性质及其图形. 能列出尚单实际问题中的函数黄 第一节:数列的极限 【、了解函数(数列)极限概念, 知识点:数列概念,数列极限的概念。 知道极限的“一6 第二章第二节:函数的极限 N”定义。了解两个极限存在准 讲 极限与 知识点:自变量挡于有限数时的极限概念,自 则、无穷小、无穷大的框念:了 12 量挡于无穷时的极阻唇,极限的基本性历 解初等函数的连续性,闭区间上 讨12 连 第三节:极限的运算法则 连续函数的性质 知识点:极限的四则运算法则,无穷小量与无 2、理解函数在一点处连续的 穷大量,极限的复合运算法则。 念,会判断间断点的类型
2 学生学会有效沟通交流,增强其团队合作意识,提高学生的实践能力、创造能力、就业能 力和创业能力。 2.课程目标 根据课程的主要任务,现确定高等数学 B1 课程目标如下: 课程目标 1:掌握经济管理中有关问题所需的微积分相关基础理论知识。 熟练掌握微积分的相关基础理论知识,培养学生对相关数学概念、定理及一些结论的 理解能力和逻辑推理能力。 课程目标 2:提升在经济管理等各方面解决相关问题所需的计算能力及应用能力。 熟练掌握微积分中遇到的各种计算问题的计算方法,并能够以此为工具分析和处理经 济管理中的实际问题。通过计算结果,能准确地分析其在经济管理中的意义。 三、课程教学内容与学时分配 序 号 知识单 元/章节 知识点 教学基本要求 推 荐 学 时 教 学 方 式 支 撑 课 程 目 标 1 第 一 章 函数 第一节:集合与函数 知识点:集合、区间与邻域、函数概念,函数 基本性质,反函数概念,六类基本初等函数, 复合函数概念,初等函数概念。 第二节:经济学中的常用函数 知识点:五类常见的经济函数——需求函数、 供给函数、成本函数、收入函数、利润函数。 1、了解函数的四个基本性质— —单调性、有界性、奇偶性和周 期性。 2、理解反函数、复合函数、分段 函数的概念、理解常见的经济函 数。 3、掌握复合函数的复合过程以及 基本初等函数的性质及其图形, 能列出简单实际问题中的函数关 系。 4 讲 授 讨 论 1、2 2 第 二 章 极 限 与 连续 第一节:数列的极限 知识点:数列概念,数列极限的概念。 第二节:函数的极限 知识点:自变量趋于有限数时的极限概念,自 变量趋于无穷时的极限概念,极限的基本性质。 第三节:极限的运算法则 知识点:极限的四则运算法则,无穷小量与无 穷大量,极限的复合运算法则。 1、了解函数(数列)极限概念, 知道极限的〝ε-δ〞、〝ε- N〞定义;了解两个极限存在准 则、无穷小、无穷大的概念;了 解初等函数的连续性,闭区间上 连续函数的性质。 2、理解函数在一点处连续的概 念,会判断间断点的类型。 12 讲 授 讨 论 1、2

第四节:极限存在准则与两个重要极限 3、掌异极限四则运算法则以及极 知识点:两个极限花在准则 夹逼准则、单限的一此基本计算方法(如利用 调有界准则:两个重要极限 两个重要极限公式、极限存在 第五节:无穷小的比较 期、等价无穷小作代换、初等 知识点:无穷小的比较概念,等价无穷小概念 数变形、连续性及变量代换等) 等价无穷小的性历及其应用」 会进行无穷小的比较。 第六节:函数的连线性 知识点:函数连续橱念,间断点的类型,连续 函数的运算法则 初等函数的连续性,闭区间 上连续函数的性质 第一节:导数的概念 知识点:导数概念,左右导数概念,导数的 何意义,函数可导与连续的关系。 第二节:导数的运算 知识点:函数的和(差)求导法侧、积商求写 法则,反函数的求导法则,高阶导数概念及其 、了解高阶导数的念 求法,数学归纳法求n阶导数。 第三章 复合函数求导的链式法则,基本求导法则,导 、理解导数与微分的几何意义 讲 导数与数公式表。 、握初等函数的求导(包括高 阶导数)及微分,隐函数、参数 10 第三节:隐函数及由参数方程所确定的函数的 1、2 微分 方程确定的函数的一阶,二阶导 导数 论 数的求法:会用导数的几何意义 知识点:隐函数求导法由参数方程确定的函 数的导数:隐函数和由参数方程确定的函数的 解决几何问 二阶导数求法, 第四节:函数的微分 知识点:函数微分的概含,可微的条件,微分 几何意义,微分运算法则,微分在近似计算中 的应用。 第一节:微分中值定理 知识点:罗尔定理,拉格朗日中值定理,柯西 l、了解柯西(Cauchy)中值定理 中值定理。 2、理解罗尔(Ro11er)定理和 第一节。洛必达法叫 知识点:洛必达法则,利用洛必达法则求极限 朗日 (Lagrange )中值定理, 第三节:函数的单调性与极值 会应用Lagrange中值定理:理解 函数的极值概念。 第四奇知识点:函数单调性的判别法,利用单调性证 3、堂挥利用洛苏达(L 中值定 明不绘式。函韵极伯的启义及位专法,极估存 讲 HosD1ta1)法则求极限的方法 授 理与导 在的必要条件和充分条件,极值的求法,函数 求函数的极估 14 数的应 最值及其求法,极值最值应用 掌判断函数 讨1、2 第四节:曲线的凹凸性、拐点及函数图形的描 的单调性与函数图形的凹凸性 论 用 函数图形的拐点的方法,会描经 绘 知识点:曲叫几性宁义、判别方法,拐点定 函数的图形:会求函数的边际函 数和弹性函数,掌握由边际函数 义:曲线的渐近线,函数图形的措绘 求总量函数的方法。能求解较活 第五节:导数在经济管理中的应用 知识点:边际函数的概念 经济中常用的边网 单的最大值和最小值的应用 题 函数:弹性的概仑,常见的弹性函数,需求弹 性。供给弹性
3 第四节:极限存在准则与两个重要极限 知识点:两个极限存在准则——夹逼准则、单 调有界准则;两个重要极限。 第五节:无穷小的比较 知识点:无穷小的比较概念,等价无穷小概念, 等价无穷小的性质及其应用。 第六节:函数的连续性 知识点:函数连续概念,间断点的类型,连续 函数的运算法则,初等函数的连续性,闭区间 上连续函数的性质。 3、掌握极限四则运算法则以及极 限的一些基本计算方法(如利用 两个重要极限公式、极限存在准 则、等价无穷小作代换、初等函 数变形、连续性及变量代换等); 会进行无穷小的比较。 3 第 三 章 导 数 与 微分 第一节:导数的概念 知识点:导数概念,左右导数概念,导数的几 何意义,函数可导与连续的关系。 第二节:导数的运算 知识点:函数的和(差)求导法则、积商求导 法则,反函数的求导法则,高阶导数概念及其 求法,数学归纳法求 n 阶导数。 复合函数求导的链式法则,基本求导法则,导 数公式表。 第三节:隐函数及由参数方程所确定的函数的 导数 知识点:隐函数求导法,由参数方程确定的函 数的导数;隐函数和由参数方程确定的函数的 二阶导数求法。 第四节:函数的微分 知识点:函数微分的概念,可微的条件,微分 几何意义,微分运算法则,微分在近似计算中 的应用。 1、了解高阶导数的概念。 2、理解导数与微分的几何意义。 3、掌握初等函数的求导(包括高 阶导数)及微分,隐函数、参数 方程确定的函数的一阶、二阶导 数的求法;会用导数的几何意义 解决几何问题。 10 讲 授 讨 论 1、2 4 第 四 章 中 值 定 理 与 导 数 的 应 用 第一节:微分中值定理 知识点:罗尔定理,拉格朗日中值定理,柯西 中值定理。 第二节:洛必达法则 知识点:洛必达法则,利用洛必达法则求极限。 第三节:函数的单调性与极值 知识点:函数单调性的判别法,利用单调性证 明不等式;函数极值的定义及其求法,极值存 在的必要条件和充分条件,极值的求法,函数 最值及其求法,极值最值应用。 第四节:曲线的凹凸性、拐点及函数图形的描 绘 知识点:曲线凹凸性定义、判别方法,拐点定 义;曲线的渐近线,函数图形的描绘。 第五节:导数在经济管理中的应用 知识点:边际函数的概念,经济中常用的边际 函数;弹性的概念,常见的弹性函数,需求弹 性,供给弹性。 1、了解柯西(Cauchy)中值定理。 2、理解罗尔(Roller)定理和拉 格朗日(Lagrange)中值定理, 会应用 Lagrange 中值定理;理解 函数的极值概念。 3 、 掌 握 利 用 洛 必 达 ( L ′ Hospital)法则求极限的方法; 会求函数的极值、掌握判断函数 的单调性与函数图形的凹凸性、 函数图形的拐点的方法,会描绘 函数的图形;会求函数的边际函 数和弹性函数,掌握由边际函数 求总量函数的方法,能求解较简 单的最大值和最小值的应用问 题。 14 讲 授 讨 论 1、2

第一节:不定积分的概念与性质 知占原函、不定和分的据,不定积分 1、了耀特殊期分技巧训统,对于 的几何意义 不定积分的性质,基本积分公式。 简单有理函数、三角有理式和无 直接积分法。 第五章 函数可作例题训练 讲 第二节;换元积分法 不定积知识点:第一换元法(漆微分法),第二换元 ,理解不定积分的概念,牢记 本积分公式, 0 2 3、拿握不定积分的换元积分法。 第三节:分部积分法 论 分部积分法。 知识点:分部积分公式,分部积分法的应用。 第五节:积分表的使用 知识点:积分表的使用方法。 第一节:定积分的概念与性质 了解广义积分收敛与发散的 知识点,定积分的韬念。定积分几何查义,定 念以及「数的概念及性质。 积分的运算性质、估值定理、积分中值定理。 理解定积分的概念及性质以及 第二节:微积分基本公式 定积分的几何意义,熟记微积分 知识点:积分上限函数的定义、求导,原函 公式:理解用微元分析法解决应 存在定理,微积分基本定理(牛顿一一莱布尼 用问题的方法。 兹公式)。 捉变上限积分函数及其求号 第六章第三节:定积分的计算 方法 粘卷牛顿 一莱布尼兹 讲 定积分知识点:定积分的换元法,定积分的分部积分 式,熟练运用定积分的换元积分 法与分部积分法求定积分,注音 14按 及其应 讨 12 第四节:广义积分与厂函数 定积分换元法与不定积分换元法 论 知识点:无限区间上的广义积分概念及其求法, 多间的相似性与区别,登据计 无界函数的广义积分概念及其求法,厂函数的 两种广义积分的方法 握求 概含及递推公式, 而图形的面积方法:会求已知平 第五节:定积分的应用 行截面面积的主体的体积和旋利 知识点:微元法,应用定积分求平面图形的面 体的体和:会求平面曲线的孤长 积、旋转体的体积、平面曲线的长:用定积 (包括直角坐标和参数方程形式 分求经济管理中的总量问题,贴现问愿。 下的曲线) 会用定积分求经济 管理中的总量问题。 四、课程教学方式 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解 决问题的能力,引导学生主动通过实践和自主学习获得相关的知识。 2.在教学内容上,按照章节结构系统讲述,重点分析各知识点、定义、定理,强调 知识的应用,训练学生的理解能力和计算与应用能力。 3.在教学过程中采取多媒体教学与传统板书、教具教学相结合的教学方式,提高课 堂教学信息量,增强教学的直观性。重视课后的习题练习,不定期讲解作业。 4.课内讨论和课外答疑相结合,线上线下相结合,灵活使用现代教学技术和手段
4 5 第 五 章 不 定 积 分 第一节:不定积分的概念与性质 知识点:原函数、不定积分的概念,不定积分 的几何意义,不定积分的性质,基本积分公式, 直接积分法。 第二节:换元积分法 知识点:第一换元法(凑微分法),第二换元 法。 第三节:分部积分法 知识点:分部积分公式,分部积分法的应用。 第五节:积分表的使用 知识点:积分表的使用方法。 1、了解特殊积分技巧训练,对于 简单有理函数、三角有理式和无 理函数可作例题训练。 2、理解不定积分的概念,牢记基 本积分公式。 3、掌握不定积分的换元积分法、 分部积分法。 10 讲 授 讨 论 2 6 第 六 章 定 积 分 及 其 应 用 第一节:定积分的概念与性质 知识点:定积分的概念,定积分几何意义;定 积分的运算性质、估值定理、积分中值定理。 第二节:微积分基本公式 知识点:积分上限函数的定义、求导,原函数 存在定理,微积分基本定理(牛顿――莱布尼 兹公式)。 第三节:定积分的计算 知识点:定积分的换元法,定积分的分部积分 法。 第四节:广义积分与 函数 知识点:无限区间上的广义积分概念及其求法, 无界函数的广义积分概念及其求法, 函数的 概念及递推公式。 第五节:定积分的应用 知识点:微元法,应用定积分求平面图形的面 积、旋转体的体积、平面曲线的弧长;用定积 分求经济管理中的总量问题,贴现问题。 1、了解广义积分收敛与发散的概 念以及 函数的概念及性质。 2、理解定积分的概念及性质以及 定积分的几何意义,熟记微积分 公式;理解用微元分析法解决应 用问题的方法。 3、掌握变上限积分函数及其求导 方法,熟悉牛顿――莱布尼兹公 式,熟练运用定积分的换元积分 法与分部积分法求定积分,注意 定积分换元法与不定积分换元法 之间的相似性与区别,掌握计算 两种广义积分的方法。掌握求平 面图形的面积方法;会求已知平 行截面面积的主体的体积和旋转 体的体积;会求平面曲线的弧长 (包括直角坐标和参数方程形式 下的曲线);会用定积分求经济 管理中的总量问题。 14 讲 授 讨 论 1、2 四、课程教学方式 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解 决问题的能力,引导学生主动通过实践和自主学习获得相关的知识。 2.在教学内容上,按照章节结构系统讲述,重点分析各知识点、定义、定理,强调 知识的应用,训练学生的理解能力和计算与应用能力。 3.在教学过程中采取多媒体教学与传统板书、教具教学相结合的教学方式,提高课 堂教学信息量,增强教学的直观性。重视课后的习题练习,不定期讲解作业。 4.课内讨论和课外答疑相结合,线上线下相结合,灵活使用现代教学技术和手段
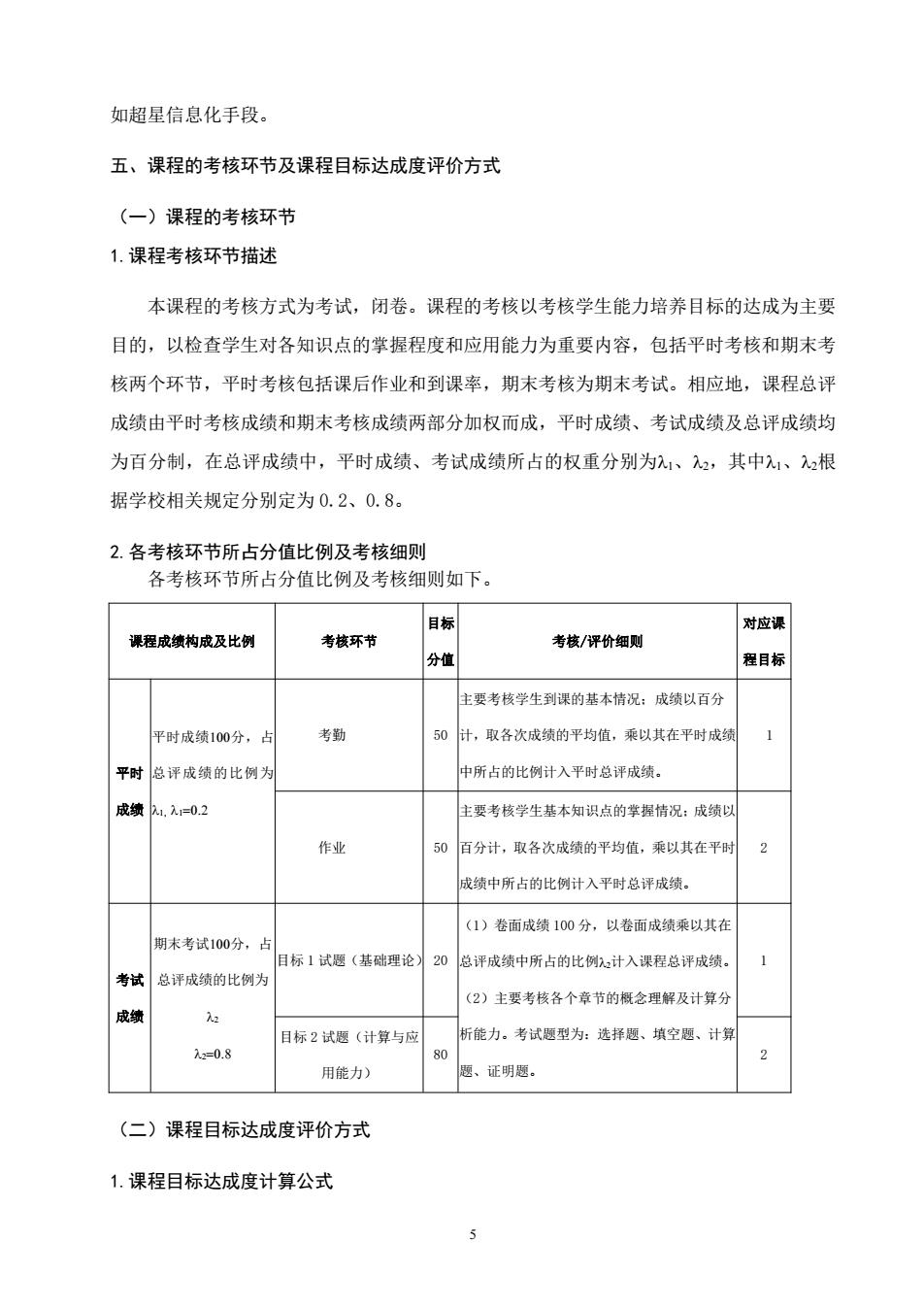
如超星信息化手段。 五、课程的考核环节及课程目标达成度评价方式 (一)课程的考核环节 1.课程考核环节描述 本课程的考核方式为考试,闭卷。课程的考核以考核学生能力培养目标的达成为主要 目的,以检查学生对各知识点的学握程度和应用能力为重要内容,包括平时考核和期末考 核两个环节,平时考核包括课后作业和到课率,期末考核为期末考试。相应地,课程总评 成绩由平时考核成绩和期末考核成绩两部分加权而成,平时成绩、考试成绩及总评成绩均 为百分制,在总评成绩中,平时成绩、考试成绩所占的权重分别为入、2,其中、2根 据学校相关规定分别定为0.2、0.8。 2.各考核环节所占分值比例及考核细则 各考核环节所占分值比例及考核细则如下。 目标 对应课 课程成绩构成及比例 考核环节 考核/评价细则 程目标 上要考核学生到课的基本情况:成绩以百分 平时成绩100分, 考勤 50计,取各次成绩的平均值,乘以其在平时成绩 平时总评成绩的比例为 中所占的比例计入平时总评成绩。 成绩1.元0.2 主要考核学生基本知识点的掌握情况:成绩以 作业 0百分计,取各次成绩的平均值,乘以其在平时 2 成绩中所占的比例计入平时总评成绩。 (1)卷面成绩100分,以卷面成绩柔以其在 期末考试100分,占 日标1试愿(基础理论 总评成绩中所占的比例计入课程总评成绩 考试总评成绩的比例为 (2)主要考核各个章节的概念理解及计算分 目标2试题(计算与应 析能力。考试题型为:选择题、填空惠、计算 =0.8 用能力) 题、证明题 (二)课程目标达成度评价方式 1.课程目标达成度计算公式
5 如超星信息化手段。 五、课程的考核环节及课程目标达成度评价方式 (一)课程的考核环节 1.课程考核环节描述 本课程的考核方式为考试,闭卷。课程的考核以考核学生能力培养目标的达成为主要 目的,以检查学生对各知识点的掌握程度和应用能力为重要内容,包括平时考核和期末考 核两个环节,平时考核包括课后作业和到课率,期末考核为期末考试。相应地,课程总评 成绩由平时考核成绩和期末考核成绩两部分加权而成,平时成绩、考试成绩及总评成绩均 为百分制,在总评成绩中,平时成绩、考试成绩所占的权重分别为、,其中、根 据学校相关规定分别定为 0.2、0.8。 2.各考核环节所占分值比例及考核细则 各考核环节所占分值比例及考核细则如下。 课程成绩构成及比例 考核环节 目标 分值 考核/评价细则 对应课 程目标 平时 成绩 平时成绩分,占 总评成绩的比例为 , 考勤 50 主要考核学生到课的基本情况;成绩以百分 计,取各次成绩的平均值,乘以其在平时成绩 中所占的比例计入平时总评成绩。 1 作业 50 主要考核学生基本知识点的掌握情况;成绩以 百分计,取各次成绩的平均值,乘以其在平时 成绩中所占的比例计入平时总评成绩。 2 考试 成绩 期末考试分,占 总评成绩的比例为 目标 1 试题(基础理论) 20 (1)卷面成绩 100 分,以卷面成绩乘以其在 总评成绩中所占的比例计入课程总评成绩。 (2)主要考核各个章节的概念理解及计算分 析能力。考试题型为:选择题、填空题、计算 题、证明题。 1 目标 2 试题(计算与应 用能力) 80 2 (二)课程目标达成度评价方式 1.课程目标达成度计算公式
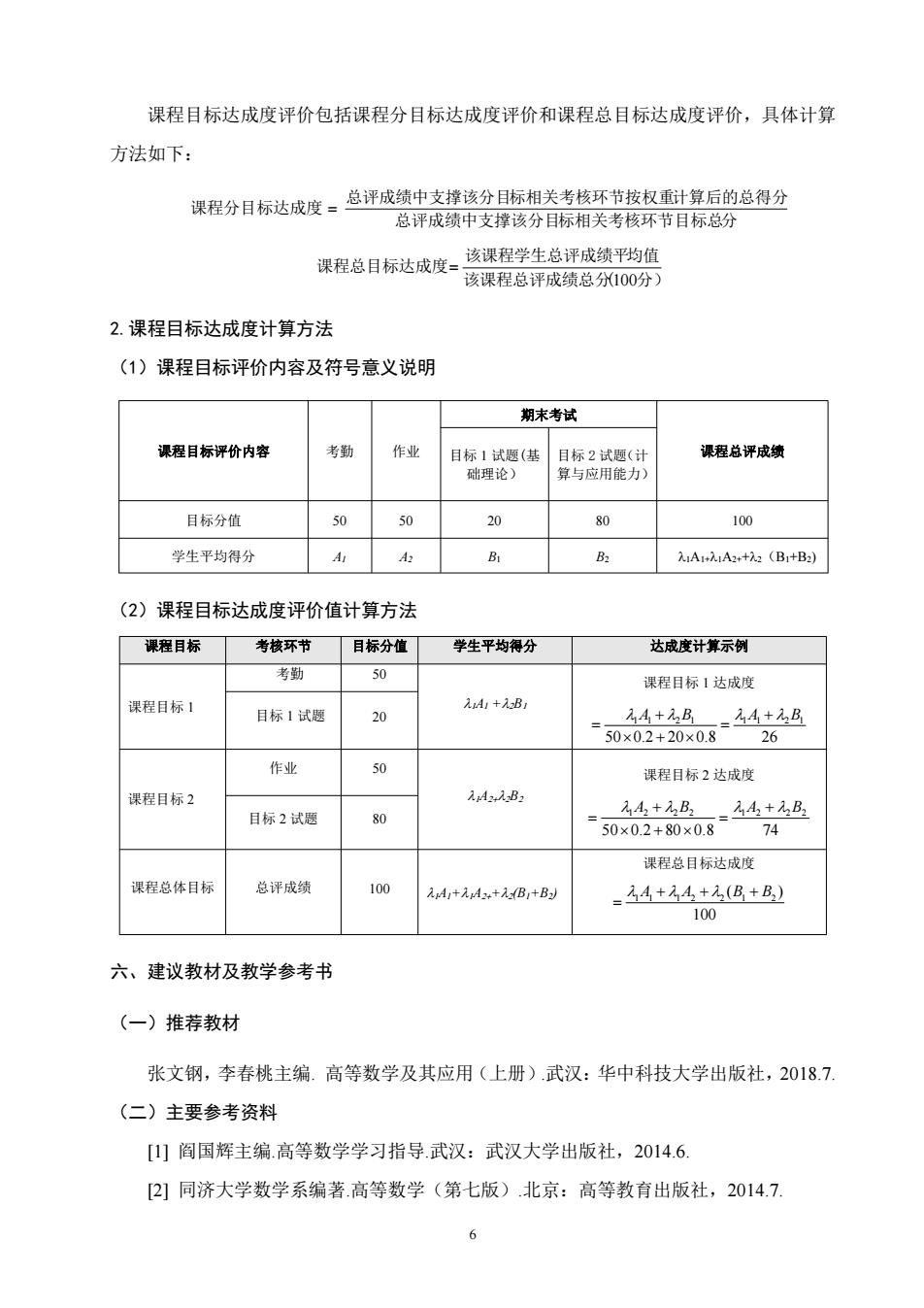
课程目标达成度评价包括课程分目标达成度评价和课程总目标达成度评价,具体计算 方法如下: 课程分目标达成度。总评成绩中支撑该分目际相关考核环节按权重计算后的总得分 总评成绩中支撑该分目标相关考核环节目标总分 课程总目标达成度= 该课程学生总评成绩平均值 该课程总评成绩总分100分) 2.课程目标达成度计算方法 (1)课程目标评价内容及符号意义说明 期末考试 课程目标评价内容 作业 目标1试趣(基目标2试趣( 课程总评成绩 础理论) 算与应用能力 目标分值 50 50 20 80 100 学生平均得分 B 入1A+:A:+3(B1+B2) (2)课程目标达成度评价值计算方法 课程目标 考核环节目标分值 学生平均得分 达成度计算示例 考勤 50 课程目标1达成度 程日标1 标1试腿 20 d+B 2A+2B 作业 课程目标2达成度 误程目标2 4,B 目标2试题 4+B 4+B 50×0.2+80×0.81 74 课程总目标达成度 课程总体目标 总评成绩 Ar+iA:.+A:(Br+B =34+4+(8+B) 100 六、建议教材及教学参考书 (一)推荐教材 张文钢,李春桃主编.高等数学及其应用(上册)武汉:华中科技大学出版社,20187 (二)主要参考资料 [山阁国辉主编高等数学学习指导.武汉:武汉大学出版社,2014.6 [2]同济大学数学系编著.高等数学(第七版)北京:高等教有出版社,2014.7. 6
6 课程目标达成度评价包括课程分目标达成度评价和课程总目标达成度评价,具体计算 方法如下: 总评成绩中支撑该分目标相关考核环节目标总分 总评成绩中支撑该分目标相关考核环节按权重计算后的总得分 课程分目标达成度 该课程总评成绩总分( 分) 该课程学生总评成绩平均值 课程总目标达成度 100 2.课程目标达成度计算方法 (1)课程目标评价内容及符号意义说明 (2)课程目标达成度评价值计算方法 课程目标 考核环节 目标分值 学生平均得分 达成度计算示例 课程目标 1 考勤 50 A1 +B 课程目标 1 达成度 50 0.2 20 0.8 26 1A1 2B1 1A1 2B1 目标 1 试题 20 课程目标 2 作业 50 AB 课程目标 2 达成度 50 0.2 80 0.8 74 1A2 2B2 1A2 2B2 目标 2 试题 80 课程总体目标 总评成绩 100 A1+A+(B1+B2) 课程总目标达成度 100 ( ) 1A1 1A2 2 B1 B2 六、建议教材及教学参考书 (一)推荐教材 张文钢,李春桃主编. 高等数学及其应用(上册).武汉:华中科技大学出版社,2018.7. (二)主要参考资料 [1] 阎国辉主编.高等数学学习指导.武汉:武汉大学出版社,2014.6. [2] 同济大学数学系编著.高等数学(第七版).北京:高等教育出版社,2014.7. 课程目标评价内容 考勤 作业 期末考试 目标 1 试题(基 课程总评成绩 础理论) 目标 2 试题(计 算与应用能力) 目标分值 50 50 20 80 100 学生平均得分 A1 A2 B1 B2 A1+A2++(B1+B2)

[3)同济大学数学系编著微积分(第三版).北京:高等牧育出版社,2010.12. 七、其他说明 无 执笔人(签字): 年月日 审核人(签字): 年月日
7 [3] 同济大学数学系编著.微积分(第三版).北京:高等教育出版社,2010.12. 七、其他说明 无 执笔人(签字): 年 月 日 审核人(签字): 年 月 日