南京大学：《离散数学 Discrete Mathmatics》课程教学资源（课件讲稿，2018）关系——第13章 关系的闭包、等价关系

关系的闭包、等价关系 离散数学一集合论 南京大学计算机科学与技术系

关系的闭包、等价关系 离散数学－集合论 南京大学计算机科学与技术系

殿原 回顾 ●关系：笛卡尔积的子集 ·函数的定义 关系的运算 ● 子集的像 。 集合运算；复合运算；逆 。单射与满射 ·0-1矩阵运算 ·反函数 关系的性质 ·自反，反自反，对称，反对 ●函数的复合 称，传递 ·函数加法与乘法 。图特征；矩阵特征

回顾  关系：笛卡尔积的子集  关系的运算  集合运算；复合运算；逆  0-1矩阵运算  关系的性质  自反，反自反，对称，反对 称，传递  图特征；矩阵特征  函数的定义  子集的像  单射与满射  反函数  函数的复合  函数加法与乘法

款售角 提要 ●闭包的定义 ·闭包的计算公式 ●传递闭包的Warshall算法 ·等价关系 ●等价类 ·划分

提要  闭包的定义  闭包的计算公式  传递闭包的Warshall算法  等价关系  等价类  划分

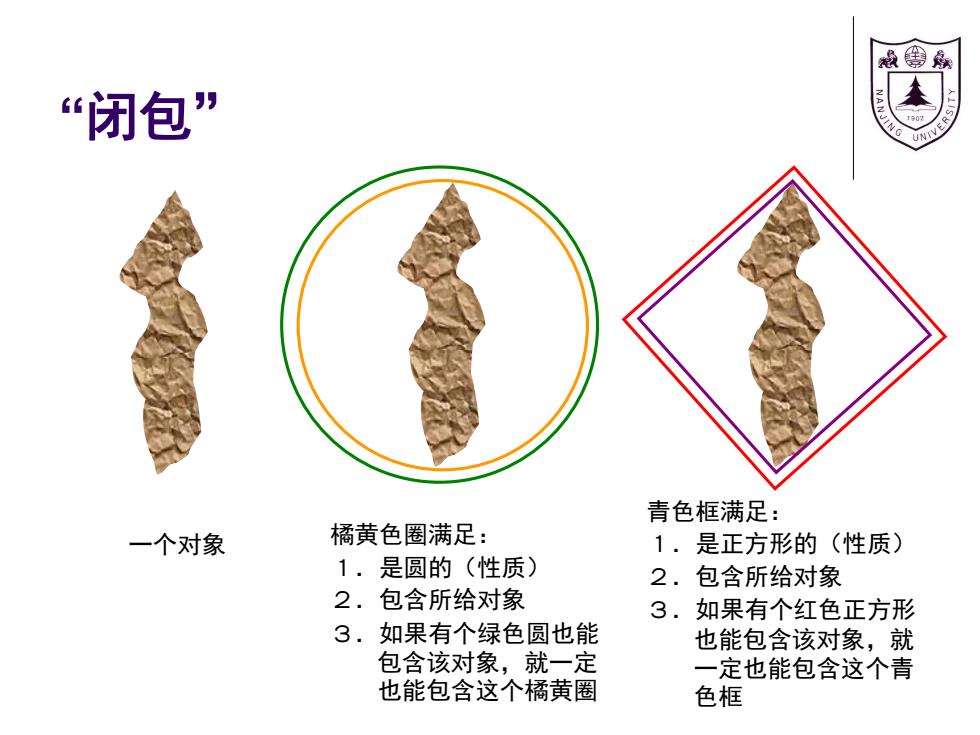
殿原 “闭包” 青色框满足： 一个对象 橘黄色圈满足： 1.是正方形的（性质） 1.是圆的（性质） 2.包含所给对象 2.包含所给对象 3.如果有个红色正方形 3.如果有个绿色圆也能 也能包含该对象，就 包含该对象，就一定 一定也能包含这个青 也能包含这个橘黄圈 色框

“闭包” 一个对象 橘黄色圈满足： １．是圆的（性质） ２．包含所给对象 ３．如果有个绿色圆也能 包含该对象，就一定 也能包含这个橘黄圈 青色框满足： １．是正方形的（性质） ２．包含所给对象 ３．如果有个红色正方形 也能包含该对象，就 一定也能包含这个青 色框

关系的闭包：一般概念 ●设R是集合A上的关系，P是给定的某种性质（如： 自反、对称、传递)，满足下列所有条件的关系R, 称为R的关于P的闭包： RCR ●R满足性质P ●如果存在集合A上的关系R',R'满足性质P并包含R,则 RCR' ·自反闭包(R)、对称闭包s(R)、传递闭包R)

关系的闭包：一般概念  设R是集合A上的关系，P是给定的某种性质（如： 自反、对称、传递），满足下列所有条件的关系R1 称为R的关于P的闭包:  RR1  R1 满足性质P  如果存在集合A上的关系R’，R’ 满足性质P 并包含R，则 R1R’  自反闭包r(R)、对称闭包s(R)、传递闭包t(R)

售嘉 自反闭包的定义 ●设R的是集合A上的关系，其自反闭包r(R)也是A 上的关系，且满足： 。(R)满足自反性； OR三r(R); ●对A上的任意关系R',若R也满足自反性，且也包含R,则 rR)CR ·例子 令A={1,2,3},R={1,1),(1,3),(2,3),(3,2)}。则(R)={(1,1), (1,3),(2,3)2(3,2),(2,2),(3,3)}

自反闭包的定义  设 R的是集合A上的关系，其自反闭包r(R)也是A 上的关系，且满足：  r(R)满足自反性；  R  r(R);  对A上的任意关系R’, 若R’也满足自反性，且也包含R，则 r(R)R’  例子  令A={1,2,3}, R={(1,1), (1,3), (2,3), (3,2)}。则r(R)={(1,1), (1,3), (2,3), (3,2), (2,2), (3,3)}

急雪扇 自反闭包的计算公式 ●(R)=ROIA IA是集合A上的恒等关系 (证明所给表达式满足自反闭包定义中的三条性质) 1.对任意x∈A,(x,x)EI4,因此，(x,x)∈RUI4 2.RCROI 3.设R集合A上的自反关系，且RcR',则对 任意(x,y)∈RUI4有(xy)∈R,或者(x,y)∈IA 对两种情况，均有(x,y)∈R',因此，RUI4R

自反闭包的计算公式  r(R) = RIA , IA是集合A上的恒等关系 (证明所给表达式满足自反闭包定义中的三条性质) 1. 对任意 xA, (x,x)IA , 因此, (x,x)RIA 2. RRIA 3. 设 R’ 集合A 上的自反关系，且RR’, 则对 任意 (x,y)RIA , 有(x,y)R, 或者 (x,y)IA。 对两种情况，均有 (x,y)R’, 因此, RIAR’

对称闭包的计算公式 ·s(R)=RURl,这里RI是R的逆关系 ·s(R)是对称的。对任意xyEA,如果(x,y)Es(R),则(x,y)ER或 者(x,y)∈R-l,即y,x)∈R1,或者Oy,x)∈R,y,x)Es(R) ●RCS(R) ●设R是集合A上的对称关系，并且RcR',则对任意(x,y)∈s(R), 有(x,y)∈R,或者(x,y)∈R1 ●情况1：(x,y)∈R,则(x,y)∈R ·情况2：(x,y)∈R1,则Oy,x)∈R,于是y,x)∈R’。根据R的对称 性：(xy)∈R 因此，s(R)二R

对称闭包的计算公式  s(R) = RR-1 , 这里R-1是R的逆关系  s(R)是对称的。对任意 x,yA, 如果 (x,y)s(R), 则(x,y)R 或 者(x,y) R-1 , 即(y,x) R-1 , 或者 (y,x) R,  (y,x)s(R)  R s(R)  设R’是集合A上的对称关系, 并且RR’, 则对任意(x,y)s(R), 有(x,y) R, 或者(x,y) R-1 .  情况1: (x,y) R, 则 (x,y) R’  情况2: (x,y) R-1 , 则 (y,x) R, 于是 (y,x) R’ 。根据R’的对称 性：(x,y) R’ 因此, s(R) R’

连通关系 ●R是集合A上的关系 ●定义集合A上的“R连通”关系R*如下： ● 对任意a,b∈A,aRb当且仅当：存在t1,2.(∈A(k是正整 数)，满足(a,)∈R,(t1,)eR,;(4,b)eR。(可以表述为： 从a到b之间存在长度至少为1的通路) ●显然：对任意a,b∈A,aR*b当且仅当存在某个正整数k, 使得aRb。 。于是：R*=RUR2UR3U.RU..= R

连通关系  R是集合A上的关系  定义集合A上的“R连通”关系R*如下：  对任意a,bA, a R*b 当且仅当：存在t1 ,t2…tk A(k是正整 数)，满足(a,t1 ) R; (t1 ,t2 )R;…; (tk ,b)R。(可以表述为： 从a到b之间存在长度至少为1的通路)  显然：对任意a,bA, a R*b 当且仅当存在某个正整数k, 使得aRkb。  于是：R* = R1R2R3…Ri… = k k R  1

传递闭包 190 1(R)=R* 1.若(xy)∈R*,(y,2)∈R*,则有S1,S2,,S,以及t,t2,,4, 满足：(x,S),…,(s,y),(y,t)2…,(,2)∈R, 因此，（x,z)∈R*. 2.RCR 3.设R是集合A上的传递关系，且包含R。若(x,y)∈R, 则有t,t2,,t,满足：(x,t)2…,(t,y)∈R, 于是(x,t),(t,2),…,(t,y)∈R 根据R的传递性，(x,y)∈R

传递闭包 t(R)  R* ,( , ) *. ( , ), ,( , ),( , ), ,( , ) , 1. ( , ) *,( , ) *, , ,..., , ,..., , 1 1 1 2 1 2 x z R x s s y y t t z R x y R y z R s s s t t t j k j k     因此 满足： 若 则有 以及   ' ( , ) '. ( , ),( , ), ,( , ) ' , ,..., , ( , ), ,( , ) , 3. ' , ( , ) , 2. 1 1 2 1 2 1 * * R x y R x t t t t y R t t t x t t y R R A R x y R R R k k k      根据 的传递性， 于是 则有 满足： 设 是集合 上的传递关系 且包含 。若  