
南京大学计算机科学与技术系 离散概率 离散数学课程组 南京大学计算机科学与技术系
南京大 学计算机 科学与技术系 离 散 概 率 离散数学课程组 南京大学计算机科学与技术系
离散数学:离散概率 提要 。直觉概率分析:三门问题 。直觉的形式化:概率空间 。条件概率与贝叶斯定理 ·随机变量及其期望与方差
离 散 数 学 : 离散概率 直觉概率分析:三门问题 直觉的形式化:概率空间 条件概率与贝叶斯定理 随机变量及其期望与方差 提要

离散数学:离散概率 三门问题(Monty Hall Problem) LETS M:UKoE D西 3
离 散 数 学 : 离散概率 三门问题(Monty Hall Problem)

离散数学:离散概率 三门问题(Monty Hall Problem) 。1 假设你正在参加一个有奖游戏。 ·你被要求在三扇门中选择一扇,其中一扇后面有一辆 车,其余两扇后面则是山羊: ·你选择了一道门; ·然后知道门后面有什么的主持人,开启了另一扇后面 有山羊的门。 ·他然后问你:“你想改变主意而选择剩下来的这个门 吗?” ·问题是:改变选择对你来说有利吗?
离 散 数 学 : 离散概率 • 假设你正在参加一个有奖游戏。 • 你被要求在三扇门中选择一扇,其中一扇后面有一辆 车,其余两扇后面则是山羊; • 你选择了一道门; • 然后知道门后面有什么的主持人,开启了另一扇后面 有山羊的门。 • 他然后问你:“你想改变主意而选择剩下来的这个门 吗?” • 问题是:改变选择对你来说有利吗? 三门问题(Monty Hall Problem)

离散数学:离散概率 进一步明确 ·你在三扇门中挑选一扇。你并不知道门内有什么。 ·主持人知道每扇门后面有什么。 ·主持人必须开启剩下的其中一扇门,并且必须提供你换门 的机会。 ·主持人永远都会挑一扇有山羊的门。 ▣如果你挑了一扇有山羊的门,主持人必须挑另一扇有山羊的门。 ▣如果参赛者挑了一扇有汽车的门,主持人随机(概率均匀分布)在 另外两扇门中挑一扇有山羊的门。 ·你会被问是否保持原来选择,还是选择剩下的那道门
离 散 数 学 : 离散概率 你在三扇门中挑选一扇。你并不知道门内有什么。 主持人知道每扇门后面有什么。 主持人必须开启剩下的其中一扇门,并且必须提供你换门 的机会。 主持人永远都会挑一扇有山羊的门。 如果你挑了一扇有山羊的门,主持人必须挑另一扇有山羊的门。 如果参赛者挑了一扇有汽车的门,主持人随机(概率均匀分布)在 另外两扇门中挑一扇有山羊的门。 你会被问是否保持原来选择,还是选择剩下的那道门。 进一步明确

离散数学:离散概率 直觉的概率分析 ·四步法 l.选定样本空间(Find the sample space) 2.定义相关事件(Define events of interests) 3.确定结果概率(Determine outcome probabilities) 4.计算事件概率(Compute event probabilities)
离 散 数 学 : 离散概率 四步法 1. 选定样本空间 (Find the sample space) 2. 定义相关事件 (Define events of interests) 3. 确定结果概率 (Determine outcome probabilities) 4. 计算事件概率 (Compute event probabilities) 直觉的概率分析

离散数学:离散概率 第一步:选定样本空间 ·试验:从一组可能的结果中得出一个结果的过程 ▣试验的某个特定“结果”通常是由若干随机因素的某 种选择而导致的。这里 ▣因素一:车在哪个门后? ▣因素二:你开始选的哪个门? ▣因素三:主持人打开哪个门? ·样本空间:所有可能结果的集合
离 散 数 学 : 离散概率 试验:从一组可能的结果中得出一个结果的过程 试验的某个特定“结果”通常是由若干随机因素的某 种选择而导致的。这里 因素一:车在哪个门后? 因素二:你开始选的哪个门? 因素三:主持人打开哪个门? 样本空间:所有可能结果的集合 第一步: 选定样本空间
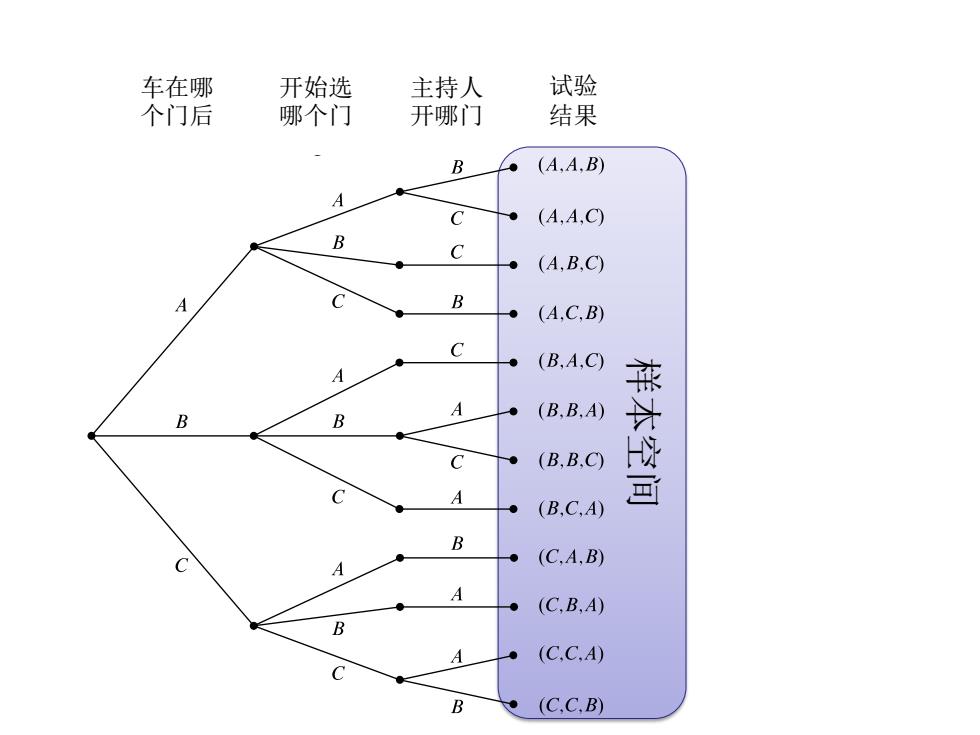
车在哪 开始选 主持人 试验 个门后 哪个门 开哪门 结果 B (A.A,B) A C ● (A,A,C) 夕 C (A,B.C) A C B (A.C,B) C A (B,A,C) A 】 B B (B.B.A) C (B,B.C) H C A (B.C.A) B (C.A,B) (C.B,A) 6 (C.C.A) C B (C.C.B)
样本空间 车在哪 个门后 开始选 哪个门 主持人 开哪门 试验 结果

离散数学:离散概率 第二步:定义相关事件 ·事件:样本空间的一个子集 回例如: ▣车在C门后:{C,A,B),(C,B,A),(C,C,A),(C,C,B)} 口第一次就选中有车的门: {(A,A,B),(A,A,C),(B,B,A),(B,B,C),(C,C,A),(C,C,B)} ▣改变选择才赢的情况: {(A,B,C),(A,C,B),(B,A,C),B,C,A),(C,A,B),(C,B,A)} 6对6,似乎换不换都一样 X
离 散 数 学 : 离散概率 第二步:定义相关事件 事件:样本空间的一个子集 例如: 车在C门后:{(C, A, B), (C, B, A), (C, C, A), (C, C, B) } 第一次就选中有车的门: {(A, A, B), (A, A, C), (B, B, A), (B, B, C), (C, C, A), (C, C, B)} 改变选择才赢的情况: {(A, B, C), (A, C, B), (B, A, C), (B, C, A), (C, A, B), (C, B, A)} 6对6,似乎换不换都一样?

离散数学:离散概率 第三步:确定结果概率 B1/2·(A,A,B)1/18 ·给每个边确定概率 A1/3 C12·(A,A,C1/18 B1/3 .C1·(A,B.C1/9 A1/3 C1B。B1·(A.C,B)1/9 A I 。C1·(B,A.C1/9 B1/3 B1/3 A1/2·(B,B,A)1/18 ·计算各结果概率 C12·(B,B,C)1/18 Pr[(A,B,B)] C1B。A1。(B.C,A01/9 1111 C1/3 4e81GA.B19 332=18 。A1·(C,B.A)1/9 B1/3 A12·(C,C,A)1/18 c1/3 B1/2·(C,C,B)1/18
离 散 数 学 : 离散概率 给每个边确定概率 计算各结果概率 Pr 𝐴, 𝐵, 𝐵 = 1 3 ⋅ 1 3 ⋅ 1 2 = 1 18 第三步:确定结果概率