南京大学：《离散数学 Discrete Mathmatics》课程教学资源（课件讲稿，2018）计数与离散概率——第10章 基本计数技术

计数 南京大学离散数学教学组

计数 南京大学离散数学教学组

款雪扇 回顾 ·布尔函数 ·代数系统与布尔代数 ·作为有补分配格的布尔代数 ·布尔代数与逻辑电路

回顾  布尔函数  代数系统与布尔代数  作为有补分配格的布尔代数  布尔代数与逻辑电路

&食感 提要 ·集合计数 ·容斥原理 ●鸽笼原理 ·排列与组合

提要  集合计数  容斥原理  鸽笼原理  排列与组合

毁 集合用于分类 ING 将属于某个集合的元素理 解为“具有某种性质”的 E F 对象，则属于该集合的补 集的元素则是“不具有某 EOF 种性质”的对象。 例如： 将全班同学的集合视为全集。 其子集E是学英语的同学的集 合，或理解为满足性质E的对 既学英语，又学法语的同学 象的集合。类似地，F是学法 语的同学的集合，即满足性质 F的对象的集合

集合用于分类 既学英语，又学法语的同学 E F EF 将属于某个集合的元素理 解为“具有某种性质”的 对象，则属于该集合的补 集的元素则是“不具有某 种性质”的对象。 例如： 将全班同学的集合视为全集。 其子集E是学英语的同学的集 合，或理解为满足性质E的对 象的集合。类似地，F是学法 语的同学的集合，即满足性质 F的对象的集合

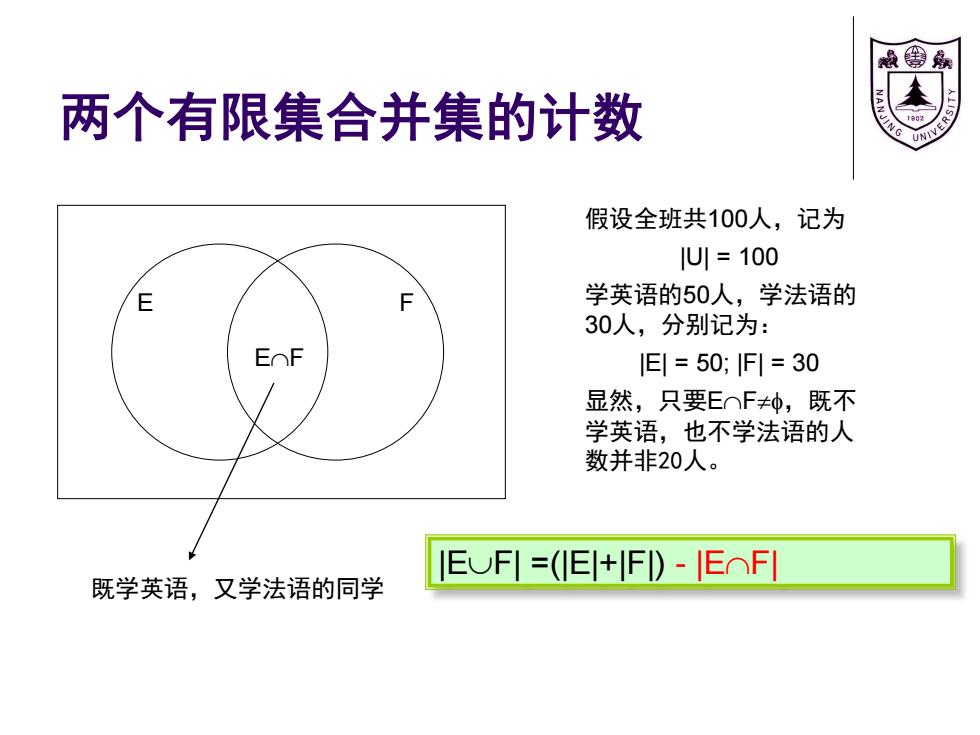
两个有限集合并集的计数 假设全班共100人，记为 U1=100 F 学英语的50人，学法语的 30人，分别记为： E=50;F1=30 显然，只要E⌒F≠种，既不 学英语，也不学法语的人 数并非20人。 IEUFI=(IE+FI)-JEOFI 既学英语，又学法语的同学

两个有限集合并集的计数 既学英语，又学法语的同学 E F EF 假设全班共100人，记为 |U| = 100 学英语的50人，学法语的 30人，分别记为： |E| = 50; |F| = 30 显然，只要EF，既不 学英语，也不学法语的人 数并非20人。 |EF| =(|E|+|F|) - |EF|

多少种排法？ 。将0,1,2，，9排成一列，要求第1个数字大于1，最后一 个数字小于8，共有多少种排法？ 。这10个数字所有的排法构成全集U,U=10! 。第1个数字不大于1的排法构成子集A(即所有以0或者1开头的排法)， 1A=29! 。最后一个数字不小于8的排法构成子集B(即所有以8或者9结末的 排法)，B=2·9! ●AnB=228! 。题目要求的排法构成子集(~A⌒~B) I~An~B1=U|-IAUB|=U|-A-IB|+IAnB=10！-49！ +4•8！=2,338,560

多少种排法？  将0,1,2,...,9排成一列，要求第1个数字大于1，最后一 个数字小于8，共有多少种排法？  这10个数字所有的排法构成全集U, |U|=10!  第1个数字不大于1的排法构成子集A(即所有以0或者1开头的排法), |A|=29!  最后一个数字不小于8的排法构成子集B(即所有以8或者9结束的 排法), |B|=29!  |AB|=228!  题目要求的排法构成子集(~A~B)  |(~A~B)| = |U| - |AB| = |U| -|A| - |B| + |AB| = 10! - 49! + 48! = 2,338,560

三个有限集合并集的计数 ·假设定义全集的三个子集A,B,C。则： JAUBUC=|A+|B|+IC-IA∽B-HA∽C-HIB∽C+|A⌒B∽CI 证明： JAUBOCI=JAUBI+CI-(AUB)OC] =lA+BHA⌒B+|C-H(A∽CU(B∽C)I =lA+|B-IA∽B+C-I(A∽C)H(B∽C)+l(A⌒B∽C)I =IA+lB+C-IAB-HA∽C-HB∽C+|AnB∽CI

三个有限集合并集的计数  假设定义全集的三个子集A,B,C。则： |ABC|=|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC| 证明： |ABC|=|AB|+|C|-|(AB)C| =|A|+|B|-|AB|+|C|-|(AC)(BC)| =|A|+|B|-|AB|+|C| - |(AC)|-|(BC)|+|(ABC)| =|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC|

关于选课的例子 。全班共有160个学生 。选数学课64人，选计算机课94人，选金融课58人 。选数学与金融的28人，选数学与计算机的26人，选 计算机与金融的22人 ·三种课全选的14人。 ·问：这三种课都没选的是多少？只选一门计算 机的有多少？

关于选课的例子  全班共有160个学生  选数学课64人，选计算机课94人，选金融课58人  选数学与金融的28人，选数学与计算机的26人，选 计算机与金融的22人  三种课全选的14人。  问：这三种课都没选的是多少？只选一门计算 机的有多少？

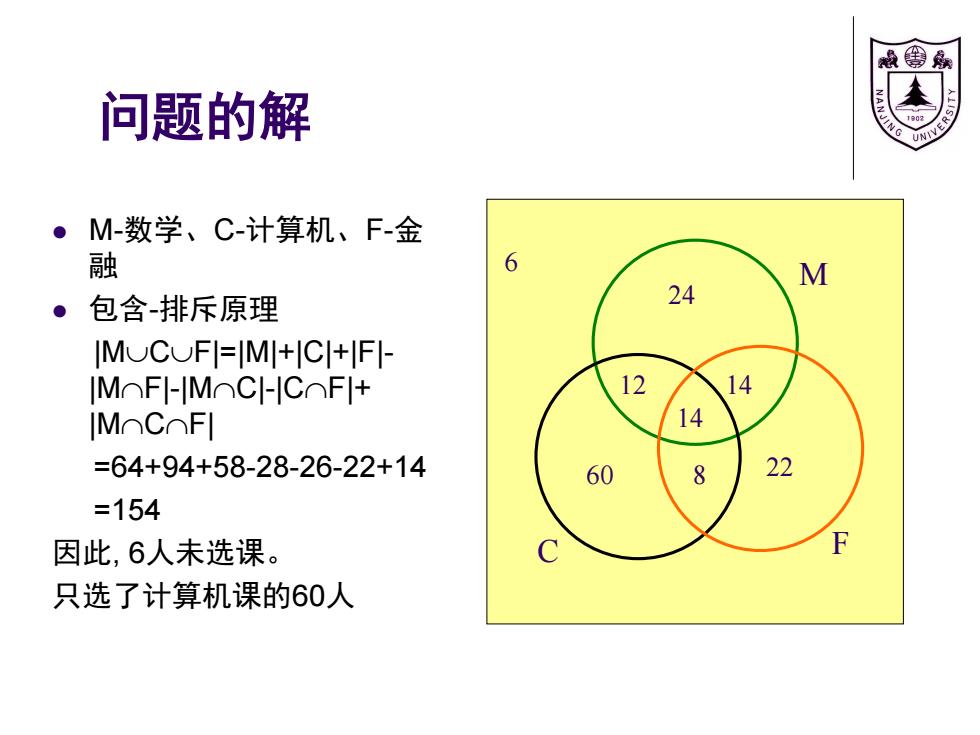
般国嘉 问题的解 ● M-数学、C-计算机、F-金 融 6 M ·包含-排斥原理 24 MOCUFI=MI+C+FI IMOFI-MOCH-COFI+ 12 14 IMC⌒FI 14 =64+94+58-28-26-22+14 60 8 22 =154 因此，6人未选课。 只选了计算机课的60人

问题的解  M-数学、C-计算机、F-金 融  包含-排斥原理 |MCF|=|M|+|C|+|F|- |MF|-|MC|-|CF|+ |MCF| =64+94+58-28-26-22+14 =154 因此, 6人未选课。 只选了计算机课的60人 M C F 14 12 14 8 24 60 22 6

容斥原理 毁扇 (Principle of Inclusion and Exclusion 假设A,A,,An是n个有限集合，则它们的拼集的元素个数是： UA,=S,-S2+S3-+(-1)S6++(-1)S i=1 其中，S6=∑1A∩A,∩∩A1k=1,2…n 1si≤i2≤.≤ik≤n 例如：4个子集的公式为： A+IA21+IA3l+A4I -(IA1∩A2l+|A∩A3+A∩A4+|A2∩A3l+A2∩A4+lA3A4I) +(A1∩A2∩A3l+lA∩A2∩A4+lA1∩A3∩A4l+lA2∩A3A4l) -IA∩A2A3nA4l

容斥原理 (Principle of Inclusion and Exclusion )                   i i i n k i i i n n k k n k k S A A A k n S S S S S A A A 1 ... -1 -1 1 2 3 n i 1 i 1 2 1 2 1 2 | ... | 1,2,..., A - -... ( 1) ... ( 1) , ,..., n 其中， 假 设 是 个有限集合，则它们的并集的元素个数是：  例如：4个子集的公式为： |A1 |+ |A2 |+ |A3 |+ |A4 | - (|A1A2 |+|A1A3 |+|A1A4 |+|A2A3 |+|A2A4 |+|A3A4 |) + (|A1A2A3 |+|A1A2A4 |+|A1A3A4 |+|A2A3A4 |) - |A1A2A3A4 |