
回顾 。 插值:给定数据点,找出多项式经过所有点 -对于n个数据点,有且仅有一个 -存在性:拉格朗日插值方法 - 唯一性:代数基本定理 一龙格现象:等距采样 -插值的不可预测性的应用:分享秘密、自纠错码(Reed-Solomon code) 函数逼近/拟合:给定函数,找出与之相近的函数(多项式) - Neierstrass定理:对于连续函数,多项式可以任意地逼近(即使是等 距采样) 这节课: · Chebyshev:多项式 ·最小二乘法 4
回顾 • 插值:给定数据点,找出多项式经过所有点 – 对于 �个数据点,有且仅有一个 – 存在性:拉格朗日插值方法 – 唯一性:代数基本定理 – 龙格现象:等距采样 – 插值的不可预测性的应用:分享秘密、自纠错码(Reed-Solomon code) • 函数逼近/拟合:给定函数,找出与之相近的函数(多项式) – Weierstrass定理:对于连续函数,多项式可以任意地逼近(即使是等 距采样) 这节课: • Chebyshev多项式 • 最小二乘法 4
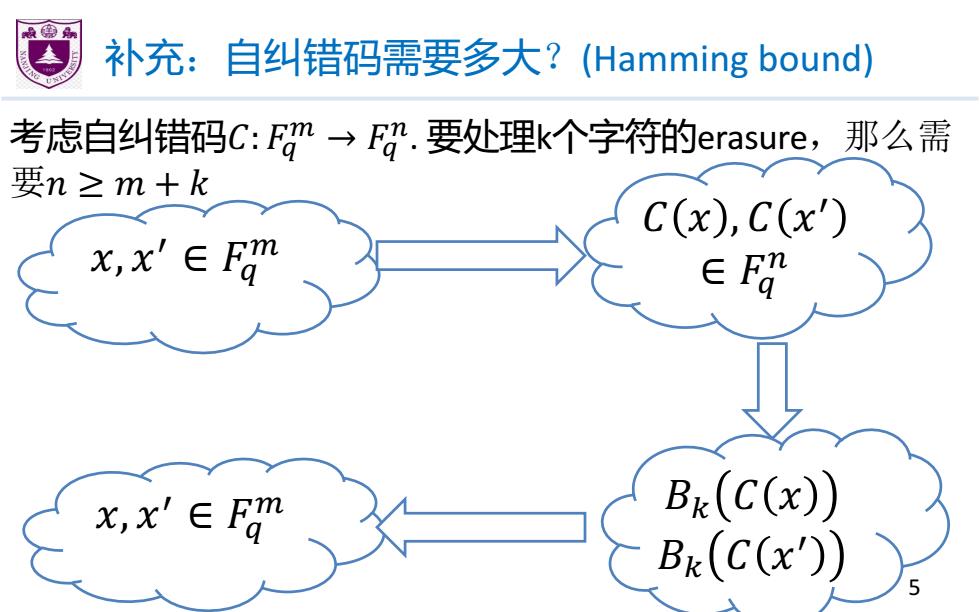
补充:自纠错码需要多大?(Hamming bound) 考虑自纠错码C:Fm→F.要处理k个字符的erasure,那么需 要n≥m+k C(x),C(x') 七,x'∈fgm x,x'∈Em Bx(C(x)) B&(C(x))
补充:自纠错码需要多大?(Hamming bound) 考虑自纠错码�: �! " → �! #. 要处理k个字符的erasure,那么需 要� ≥ � + � 5 �, �! ∈ �" # � � , � �! ∈ �" $ �, �! ∈ �" # �% � � �% � �!

补充:自纠错码需要多大?(Hamming bound) 考虑自纠错码C:Fgm→Fg.要处理k个字符的erasure,那么需要n≥ m+k 反证法:假设n≤m+k-1 考虑所有的codewordi的集合:{C(x):x∈Fm 去掉这些codeword的后面k位(投影到前面m-1位) ·剩下每个codeword的长度最多为m-1 由Pigeon-hole principle,一定存在两个codeword在前m一1位是相同 的,记为x,x 。 这意味着,存在x,x'∈Fgm,x≠x,使得C(x)和C(x)在去掉了最后 的k位后相等 这与能处理k个字符的erasurel的假设矛盾。 6
补充:自纠错码需要多大?(Hamming bound) 考虑自纠错码�: �" # → �" $. 要处理k个字符的erasure,那么需要� ≥ � + � 反证法:假设� ≤ � + � − 1 • 考虑所有的codeword的集合: � � : � ∈ �" # • 去掉这些codeword的后面 � 位 (投影到前面� − 1位) • 剩下每个codeword的长度最多为� − 1 • 由Pigeon-hole principle,一定存在两个codeword在前� − 1位是相同 的,记为�, �′ • 这意味着,存在�, �% ∈ �" # , � ≠ �′,使得� � 和 � �′ 在去掉了最后 的 � 位后相等 • 这与能处理k个字符的erasure的假设矛盾。 6

补充:自纠错码需要多大?(Hamming bound) 考虑自纠错码C:Fm→F.要处理k个字符的corruption,那么需要n≥m+2k 反证法:假设n≤m+2k-1 ·考虑所有的codeword的集合:{C(x):x∈Fgm} ·去掉这些codeword的后面2k位(投影到前面m-1位) ·剩下每个codeword的长度最多为m-1 由Pigeon-hole principle,.一定存在两个codeword在前m-1位是相同的,记为x,x' ·这意味着,存在x,x'∈Fm,x≠x',使得C(x)和C(x)在去掉了最后的2k位后相等 因此,可以从C(x)修改最多k个字符,再从C(x)修改最多k个字符,将得到一样的 信息 ,将无法区分这是由C(x)修改最多k个字符得到的,还是从C(x) 这与能处理k个字符的corruption矛盾 ● 7
补充:自纠错码需要多大? (Hamming bound) 考虑自纠错码�: �! " → �! #. 要处理k个字符的corruption,那么需要� ≥ � + 2� 反证法:假设� ≤ � + 2� − 1 • 考虑所有的codeword的集合: � � : � ∈ �! " • 去掉这些codeword的后面 2� 位 (投影到前面� − 1位) • 剩下每个codeword的长度最多为� − 1 • 由Pigeon-hole principle,一定存在两个codeword在前� − 1位是相同的,记为�, �′ • 这意味着,存在�, �$ ∈ �! " , � ≠ �′,使得� � 和 � �′ 在去掉了最后的 2� 位后相等 • 因此,可以从� � 修改最多�个字符,再从� �′ 修改最多�个字符,将得到一样的 信息 • 从接收者的角度看,将无法区分这是由� � 修改最多�个字符得到的,还是从� �′ 修改最多�个字符得到的 • 这与能处理k个字符的corruption矛盾 7
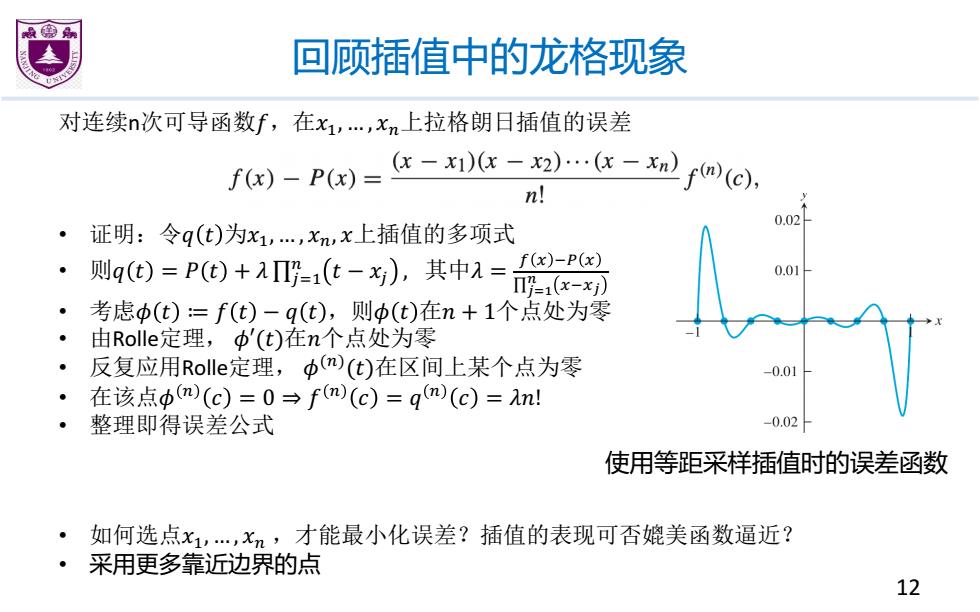
回顾插值中的龙格现象 对连续n次可导函数f,在x1,…,xn上拉格朗日插值的误差 f)-P)=区-)6x-2…x-x) f(n)(c), n! 0.02 证明:令q(t)为x1,…,x,x上插值的多项式 则q()=P(t)+Π=1(t-x),其中入=)-P 0.01 Π=1(x-x) 考虑φ(t)=f(t)-q(t),则φ(t)在n+1个点处为零 由Rolle定理,中'(t)在n个点处为零 反复应用Rolle定理,中m)(t)在区间上某个点为零 -0.01 在该点中m)(c)=0→f(c)=qm)(c)=l 整理即得误差公式 -0.02 使用等距采样插值时的误差函数 如何选点x1,,xn,才能最小化误差?插值的表现可否媲美函数逼近? ,采用更多靠近边界的点 12
回顾插值中的龙格现象 12 对连续n次可导函数�,在�!, … , �"上拉格朗日插值的误差 • 证明:令� � 为�!, … , �", �上插值的多项式 • 则� � = � � + � ∏#$! " � − �# , 其中� = % & '( & ∏!"# $ &'&! • 考虑� � ≔ � � − � � ,则� � 在� + 1个点处为零 • 由Rolle定理, �′(�)在�个点处为零 • 反复应用Rolle定理, �(") (�)在区间上某个点为零 • 在该点� " � = 0 ⇒ � " � = � " � = ��! • 整理即得误差公式 • 如何选点�!, … , �" ,才能最小化误差?插值的表现可否媲美函数逼近? • 采用更多靠近边界的点 使用等距采样插值时的误差函数

Chebyshev插值基点 不失一般性地,假设函数是定义在[-1,1]上的 目标:选取x1,…,xn使得 max I(x-x1)(x-x2)...(x-xn) (*) xe[-1,1] 最小 定理:令x=cos21严,i=1,,n,得到()最小值/2-1 2n Chebyshev多项式Tn(x)=2n-1(x-x1)(x-x2)(x-xn) Chebyshev插值多项式:选取Chebyshev基点进行拉格朗日插值得到的多 项式 13
Chebyshev插值基点 不失一般性地,假设函数是定义在[-1,1]上的 目标:选取�!, … , �"使得 max %∈[(),)] | � − �) � − �, … � − �# | (∗) 最小 • 定理:令�- = cos ,-() . ,# , � = 1, … , �,得到(∗)最小值 ⁄) ,!"# • Chebyshev多项式 �# � ≔ 2#() � − �) � − �, … � − �# • Chebyshev插值多项式:选取Chebyshev基点进行拉格朗日插值得到的多 项式 13

Chebyshev多项式 等价的定义Tn(x):=cos(n arccos x),x∈[-1,1] 这为什么是一个多项式? ·回忆三角函数的倍角公式 cos(n0)可以展开成为关于cos的n次多项式 令x=cos0,则cos(n0)是关于x的m次多项式 cos(ne)=cos(narccosx) T(x)=1 T(x)=x T2(x)=c0S20=2c0s20-1=2x2-1 14
Chebyshev多项式 等价的定义 �! � ≔ cos(� arccos �) , � ∈ [−1,1] 这为什么是一个多项式? • 回忆三角函数的倍角公式 • cos(��)可以展开成为关于 cos �的�次多项式 • 令� = cos �,则cos(��)是关于�的�次多项式 • cos �� = cos(� arccos �) �" � = 1 �# � = � �$ � = cos 2� = 2 cos$ � − 1 = 2�$ − 1 14

Chebyshev多项式 等价的定义Tn(x)=cos(n arccos x),x∈[-1,1] 令x=cos0 T0(x)=1 T(x)=x T2(x)=c0s20=2c0s20-1=2x2-1 应用倍角公式: Tn+1 (x)=cos(ne+0)=cosne cos0-sinne sin Tn-1 (x)=cos(ne-0)=cosne cos0+sinne sin0 两式相加 Tn+1 (x)+Tn-1(x)=2 cosne cos0 2xTn (x) 递归关系 Tn+1(x)=2xTn(x)-Tn-1(x) 15
Chebyshev多项式 等价的定义 �" � ≔ cos(� arccos �) , � ∈ [−1,1] 令� = cos � �# � = 1 �! � = � �$ � = cos 2� = 2 cos$ � − 1 = 2�$ − 1 应用倍角公式: �"%! � = cos �� + � = cos �� cos � − sin �� sin � �"&! � = cos �� − � = cos �� cos � + sin �� sin � 两式相加 �"%! � + �"&! � = 2 cos �� cos � = 2��" � 递归关系 �"%! � = 2��" � − �"&! � 15

Chebyshev多项式 等价的定义 T (x):=cos(narccosx),xE [-1,1] 些观察: ·次数为n,最高次项的系数是2n-1 ·Tn(1)=1,Tn(-1)=(-1)m ·lTn(x川≤1 .Th)的零点恰好是=os2,i=1,n 2n >cosn8=0ifn8=(2i-1)·Z,i=1,,n ·Tn(x)在-1到1之间来回往返n+1次,分别在 cos0,cosco 。(n-1)π ,C0Sπ 16
Chebyshev多项式 等价的定义 �! � ≔ cos(� arccos �) , � ∈ [−1,1] 一些观察: • 次数为�,最高次项的系数是2!%# • �! 1 = 1, �! −1 = −1 ! • �! � ≤ 1 • �! � 的零点恰好是 �& = cos $&%# ' $! , � = 1, … , � Øcos �� = 0 iff �� = 2� − 1 ⋅ ! " , � = 1, … , � • �! � 在-1到1之间来回往返n+1次,分别在 cos 0, cos ' ! , … , cos !%# ' ! , cos � 16

Chebyshev多项式 观察:Tn(x)在-1到1之间来回往返n+1次,分别在 cos0,cosco n,C0sπ Chebyshev定理:令x=cos2ir,i=1,,n,得到max,K-x)(x- 2n xe[-1,1] x2)(x-xn)最小值/2n-1 证明: 假设有另一组x的选择,使得Pn(x)=(x-x1)(x-x2).(x-xn)在[-1,1] 上有更小的极犬值。换言之,xe-1,1],它n(x)川</2 /2n-1o 考虑(x)-Tn(x)/2n-1则在n+1个点上的符号是正负交替的。因此 B(x)n7n(x7224有n个零点。 注意到Pn(x)和Tn(x)/2n-1都是首1的多项式(最高次系数为1) 影盾欧舞2务智n四/2-有个 17
Chebyshev多项式 观察:�# � 在-1到1之间来回往返n+1次,分别在 cos 0, cos . # , … , cos #() . # , cos � Chebyshev定理:令�- = cos ,-() . ,# , � = 1, … , �,得到 max %∈[(),)] � − �) ( ) � − �, … (� − �#)最小值 ⁄) ,!"# 证明: • 假设有另一组�-的选择,使得�# � ≔ � − �) � − �, … (� − �#)在[-1,1] 上有更小的极大值。换言之, ∀� ∈ −1,1 , |�# � | < ⁄) ,!"# 。 • 考虑�# � − �# � /2/(),则在n+1个点上的符号是正负交替的。因此 �# � − �# � /2/()有n个零点。 • 注意到 �# � 和 �# � /2/()都是首1的多项式(最高次系数为1) • �# � − �# � /2/()的次数最多为n-1次,这与�# � − �# � /2/()有�个 零点矛盾。(除非�# � − �# � /2/()为零多项式) 17