
《概率论与数理统计》 学习指导 疑难分析 例题解析 李永明 2006年3月20日
《概率论与数理统计》 学习指导 ·疑难分析 ·例题解析 李永明 2006 年 3 月 20 日

目录 第一章事件与概率 第二章离散型随机变量…1山 第三章连续型随机变量.…200 第四章大数定律与中心极限定理…2 第五章数理统计的基本概念.…5 第六章点估计. 0……38 第七章假设检验…42 第八章方差分析和回归分析…45
1 目 录 第一章 事件与概率 ...................................... 2 第二章 离散型随机变量 .............................. 111 第三章 连续型随机变量 .............................. 200 第四章 大数定律与中心极限定理 ..................... 32 第五章 数理统计的基本概念 .......................... 35 第六章 点估计 ......................................... 38 第七章 假设检验....................................... 42 第八章 方差分析和回归分析 .......................... 45

第一章事件与概率 疑难分析 1、必然事件与不可能事件 必然事件是在一定条件下必然发生的事件,不可能事件指的是在一定条件下 必然不发生的事件.它们都不具有随机性,是确定性的现象,但为研究的方便,把 它们看作特殊的随机事件. 2、互逆事件与互斥事件 如果两个事件A与B必有一个事件发生,且至多有一个事件发生,则A、B 为互逆事件:如果两个事件A与B不能同时发生,则A、B为互斥事件.因而, 互逆必定互斥,互斥未必互逆.区别两者的关键是:当样本空间只有两个事件时, 两事件才可能互逆,而互斥适用与多个事件的情形.作为互斥事件在一次试验中两 者可以都不发生,而互逆事件必发生一个且只发生一个 3、两事件独立与两事件互斥 两事件A、B独立,则A与B中任一个事件的发生与另一个事件的发生无关, 这时P(AB)=P(A)P(B):而两事件互斥,则其中任一个事件的发生必然导致另 一个事件不发生,这两事件的发生是有影响的, B 这时AB=中,P(AB)=0.可以用图形作一直观 A 解释.在图1.1左边的正方形中, 图1.1 P(4B)=P4)=2=P(B),表示样本空间中两事件的独立关系,而在右边的 正方形中,P(AB)=0,表示样本空间中两事件的互斥关系
2 第一章 事件与概率 疑 难 分 析 1、必然事件与不可能事件 必然事件是在一定条件下必然发生的事件,不可能事件指的是在一定条件下 必然不发生的事件.它们都不具有随机性,是确定性的现象,但为研究的方便,把 它们看作特殊的随机事件. 2、互逆事件与互斥事件 如果两个事件 A 与 B 必有一个事件发生,且至多有一个事件发生,则 A 、B 为互逆事件;如果两个事件 A 与 B 不能同时发生,则 A 、 B 为互斥事件.因而, 互逆必定互斥,互斥未必互逆.区别两者的关键是:当样本空间只有两个事件时, 两事件才可能互逆,而互斥适用与多个事件的情形.作为互斥事件在一次试验中两 者可以都不发生,而互逆事件必发生一个且只发生一个. 3、两事件独立与两事件互斥 两事件 A 、B 独立,则 A 与 B 中任一个事件的发生与另一个事件的发生无关, 这时 P(AB) = P(A)P(B) ;而两事件互斥,则其中任一个事件的发生必然导致另 一个事件不发生,这两事件的发生是有影响的, 这时 AB = ,P(AB) = 0 .可以用图形作一直观 解释.在图 1.1 左边的正方形中, 图 1.1 ( ) 2 1 , ( ) 4 1 P(AB) = P A = = P B ,表示样本空间中两事件的独立关系,而在右边的 正方形中, P(AB) = 0 ,表示样本空间中两事件的互斥关系. A B AB A B

4、条件概率P(AB)与积事件概率P(AB) P(AB)是在样本空间Ω内,事件AB的概率,而P(AB)是在试验E增加 了新条件B发生后的缩减的样本空间2。中计算事件A的概率,虽然A、B都发 生,但两者是不同的,一般说来,当A、B同时发生时,常用P(AB),而在有 包含关系或明确的主从关系时,用P(A|B).如袋中有9个白球1个红球,作不放 回抽样,每次任取一球,取2次,求:(1)第二次才取到白球的概率:(2)第一 次取到的是白球的条件下,第二次取到白球的概率.问题(1)求的就是一个积事 件概奉的问题,而问题(2)求的就是一个条件概率的问题。 5、全概率公式与贝叶斯Bayes)公式 当所求的事件概率为许多因素引发的某种结果,而该结果又不能简单地看作 这诸多事件之和时,可考虑用全概率公式,在对样本空间进行划分时,一定要注 意它必须满足的两个条件.贝叶斯公式用于试验结果已知,追查是何种原因(情况、 条件)下引发的概率。 例题解析 【例1】写出下列随机试验的样本空间及下列事件包含的样本点: (1)掷一棵骰子,出现奇数点. (2)投掷一枚均匀硬币两次: 1)第一次出现正面:2)两次出现同一面:3)至少有一次出现正面 (3)在1,2,3,4四个数中可重复地抽取两个数,其中一个数是另一个数 的两倍。 (4)将a,b两只球随机地放到3个盒子中去,第一个盒子中至少有一个球
3 4、条件概率 P(A| B) 与积事件概率 P(AB) P(AB) 是在样本空间 内,事件 AB 的概率,而 P(A| B) 是在试验 E 增加 了新条件 B 发生后的缩减的样本空间 B 中计算事件 A 的概率.虽然 A 、 B 都发 生,但两者是不同的,一般说来,当 A 、 B 同时发生时,常用 P(AB) ,而在有 包含关系或明确的主从关系时,用 P(A| B) .如袋中有 9 个白球 1 个红球,作不放 回抽样,每次任取一球,取 2 次,求:(1)第二次才取到白球的概率;(2)第一 次取到的是白球的条件下,第二次取到白球的概率.问题(1)求的就是一个积事 件概率的问题,而问题(2)求的就是一个条件概率的问题. 5、全概率公式与贝叶斯(Bayes)公式 当所求的事件概率为许多因素引发的某种结果,而该结果又不能简单地看作 这诸多事件之和时,可考虑用全概率公式,在对样本空间进行划分时,一定要注 意它必须满足的两个条件.贝叶斯公式用于试验结果已知,追查是何种原因(情况、 条件)下引发的概率. 例 题 解 析 【例 1】写出下列随机试验的样本空间及下列事件包含的样本点: (1)掷一棵骰子,出现奇数点. (2)投掷一枚均匀硬币两次: 1)第一次出现正面;2)两次出现同一面;3)至少有一次出现正面. (3)在 1,2,3,4 四个数中可重复地抽取两个数,其中一个数是另一个数 的两倍. (4)将 a,b 两只球随机地放到 3 个盒子中去,第一个盒子中至少有一个球

分析:可对照集合的概念来理解样本空间和样本点:样本空间可指全集,样 本点是元素,事件则是包含在全集中的子集, 解:()掷一棵骰子,有六种可能结果,如果用“1”表示“出现1点”这个 样本点,其余类似.则样本空间为:2=1,2,3,4,5,6卧,出现奇数点的事件 为:{1,3,5. (2)投掷一枚均匀硬币两次,其结果有四种可能,若用(正,反)表示“第 一次出现正面,第二次出现反面”这一样本点,其余类似.则样本空间为:2={(正, 正),(正,反),(反,正),(反,反)},用A、B、C分别表示上述事件1)、2)、 3),则事件A={(正,正),(正,反):事件B={(正,正),(反,反):事 件C={(正,正),(正,反),(反,正)} (3)在1,2,3,4四个数中可重复地抽取两个数,共有42=16种可 能,若用(位,)表示“第一次取数1,第二次取数j”这一样本点,则样本空间为: 2={(亿,)}(亿,j=1,2,3,4):其中一个数是另一个数的两倍的事件为:{(1,2), (2,1),(2,4),(4,2). (4)三个盒子分别记为甲、乙、丙,将品,b两只球随机地放到3个盒子中去共 有九种结果.若用(甲、乙)表示“a球放入甲盒,b球放入乙盒”这一样本点, 其余类似.则样本空间为:={(甲,甲),(甲,乙),(甲,丙),(乙, 乙),(乙,甲),(乙,丙),(丙,甲),(丙,乙),(丙,丙):第 个盒子中至少有一个球的事件为:{(甲,甲),(甲,乙),(甲,丙),(乙, 甲),(丙,甲)}. 【例2】设A、B、C为三个事件,用A、B、C的运算关系表示下列各事件 (1)仅A发生: (2)A与C都发生,而B不发生: (3)所有三个事件都不发生:(4)至少有一个事件发生:
4 分析:可对照集合的概念来理解样本空间和样本点:样本空间可指全集,样 本点是元素,事件则是包含在全集中的子集. 解:(1) 掷一棵骰子,有六种可能结果,如果用“1”表示“出现 1 点”这个 样本点,其余类似.则样本空间为: ={1,2,3,4,5,6},出现奇数点的事件 为:{1,3,5}. (2)投掷一枚均匀硬币两次,其结果有四种可能,若用(正,反)表示“第 一次出现正面,第二次出现反面”这一样本点,其余类似.则样本空间为: ={(正, 正),(正,反),(反,正),(反,反)},用 A、B、C 分别表示上述事件 1)、2)、 3),则事件 A ={(正,正),(正,反)};事件 B ={(正,正),(反,反)};事 件 C ={(正,正),(正,反),(反,正)}. (3)在 1,2,3,4 四个数中可重复地抽取两个数,共有 4 16 2 = 种可 能,若用 (i, j) 表示“第一次取数 i ,第二次取数 j ”这一样本点,则样本空间为: ={ (i, j) } (i, j =1,2,3,4) ;其中一个数是另一个数的两倍的事件为:{(1,2), (2,1),(2,4),(4,2)}. (4)三个盒子分别记为甲、乙、丙,将 a,b 两只球随机地放到 3 个盒子中去共 有九种结果.若用(甲、乙)表示“a 球放入甲盒,b 球放入乙盒”这一样本点, 其余类似.则样本空间为: ={(甲,甲),(甲,乙),(甲,丙),(乙, 乙),(乙,甲),(乙,丙),(丙,甲),(丙,乙),(丙,丙)};第一 个盒子中至少有一个球的事件为:{(甲,甲),(甲,乙),(甲,丙),(乙, 甲),(丙,甲)}. 【例 2】设 A、B、C 为三个事件,用 A、B、C 的运算关系表示下列各事件: (1)仅 A 发生; (2) A 与 C 都发生,而 B 不发生; (3)所有三个事件都不发生;(4)至少有一个事件发生;

(5)至多有两个事件发生:(6)至少有两个事件发生: (7)恰有两个事件发生:(8)恰有一个事件发生. 分析:利用事件的运算关系及性质来描述事件 解:(1)ABC:(2)ABC:(3)ABC或AUBOC:(4)AUBUC 或ABCABCABCUABCABCUABCABC:(5)AUBUC或 ABCABCUABCUABCUABCUABCUABC: (6)ABUACBC ABCUABCABCUABC (7)ABCUABCUABC:(8)ABCABCUABC. 【例3】把n个不同的球随机地放入N(N≥)个盒子中,求下列事件的概率: (1)某指定的n个盒子中各有一个球: (2)任意n个盒子中各有一个球: (3)指定的某个盒子中恰有m(m<n)个球 分析:这是古典概率的一个典型问题,许多古典概率的计算问题都可归结为 这一类型.每个球都有N种放法,n个球共有N"种不同的放法.“某指定的n个 盒子中各有一个球”相当于n个球在n个盒子中的全排列:与(1)相比,(2) 相当于先在N个盒子中选n个盒子,再放球:(3)相当于先从n个球中取m个 放入某指定的盒中,再把剩下的n一m个球放入N-1个盒中. 解:样本空间中所含的样本点数为N”. )该事件所含的样本点数是川,故:p=以:
5 (5)至多有两个事件发生; (6)至少有两个事件发生; (7)恰有两个事件发生; (8)恰有一个事件发生. 分析:利用事件的运算关系及性质来描述事件. 解:(1) ABC ;(2) ABC ;(3) ABC 或 ABC ;(4) ABC 或 ABC ABC ABC ABC ABC ABC ABC ;(5) ABC 或 ABC ABC ABC ABC ABC ABC ABC ; (6) ABACBC 或 ABC ABC ABC ABC ; (7) ABC ABC ABC ;(8) ABC ABC ABC . 【例 3】把 n 个不同的球随机地放入 N(N n) 个盒子中,求下列事件的概率: (1)某指定的 n 个盒子中各有一个球; (2)任意 n 个盒子中各有一个球; (3)指定的某个盒子中恰有 m(m n) 个球. 分析:这是古典概率的一个典型问题,许多古典概率的计算问题都可归结为 这一类型.每个球都有 N 种放法, n 个球共有 n N 种不同的放法.“某指定的 n 个 盒子中各有一个球”相当于 n 个球在 n 个盒子中的全排列;与(1)相比,(2) 相当于先在 N 个盒子中选 n 个盒子,再放球;(3)相当于先从 n 个球中取 m 个 放入某指定的盒中,再把剩下的 n−m 个球放入 N −1 个盒中. 解:样本空间中所含的样本点数为 n N . (1)该事件所含的样本点数是 n! ,故: n N n p = ! ;

(2)在N个盒子中选n个盒子有C。种选法,故所求事件的概率为: p=C (3)从n个球中取m个有Cm种选法,剩下的n-m个球中的每一个球都有 N-l种放法,故所求事件的概率为:p=C.W-1人 N 【例4】随机地向由0<y<1州<所围成的正方形内璃一点,点落在该正方形 内任何区域的概率与区域面积成正比,求原点和该点的连线与x轴正向的夹角小 于红的版率 分析:这是一个几何概率问题,通常可借助几何上的度量(长度、面积、体 积或容积等)来合理地规定其概率. 解:用S表示该正方形的面积,S表示 图1.2阴影部分面积,则所求的概率为: 0 图1.2 【例5】设事件A与B互不相容,且P(A)=p,P(B)=q,求下列事件的概率: P(AB),P(AUB),P(AB),P(AB). 分析:按概率的性质进行计算. 解:A与B互不相容,所以AB=中,P(AB)=P()=0:
6 (2)在 N 个盒子中选 n 个盒子有 n CN 种选法,故所求事件的概率为: n n N N C n p ! = ; (3)从 n 个球中取 m 个有 m Cn 种选法,剩下的 n−m 个球中的每一个球都有 N −1 种放法,故所求事件的概率为: n n m n N N N p C − − = ( 1) . 【例 4】随机地向由 2 1 0 y 1、x 所围成的正方形内掷一点,点落在该正方形 内任何区域的概率与区域面积成正比,求原点和该点的连线与 x 轴正向的夹角小 于 4 3 的概率. 分析:这是一个几何概率问题,通常可借助几何上的度量(长度、面积、体 积或容积等)来合理地规定其概率. 解:用 S 表示该正方形的面积, 1 S 表示 图 1.2 阴影部分 面积,则所求的概率为: 8 7 1 ) 2 1 ( 2 1 1 2 1 = − = = S S p . 【例 5】设事件 A 与 B 互不相容,且 P(A) = p, P(B) = q ,求下列事件的概率: P(AB), P(A B), P(AB), P(AB) . 分析:按概率的性质进行计算. 解: A 与 B 互不相容,所以 AB = , P(AB) = P() = 0 ; x y 1 2 1 2 1 − 0 图 1.2

P(A+B)=P()+P(B)=p+q:由于A与B互不相容,这时AB=A,从而 P(AB)=P()=P:由于AB=AUB,从而 P(AB)=P(AUB)=1-P(AUB)=1-(p+q). 【例6】某住宅楼共有三个孩子,己知其中至少有一个是女孩,求至少有一个是 男孩的概率(假设一个小孩为男或为女是等可能的). 分析:在已知“至少有一个是女孩”的条件下求“至少有一个是男孩”的概 率,所以是条件概率间题根据公式P(B1A)=PL4,必须求出P(AB,P氏A). P(4) 解:设A={至少有一个女孩},B={至少有一个男孩},则A={三个全是男孩} B={仁个全是女孩},于是 11 PA)=2宁-8PB,事件AB为“至少有一个女孩且至少有一个男孩”,因 为AB=AUB,且AB=D,所以P(AB)=1-P(AB)=1-P(AUB)= 1-团+P=1--P=1-闭-从面:在起砂有 3 一个为女孩的条件下,求至少有一个是男孩的概率为: 3 【例7】某电子设备制造厂所用的品体管是由三家元件制造厂提供的.根据以往的 记录有以下的数据(表1-1)
7 P(A+ B) = P(A) + P(B) = p + q ;由于 A 与 B 互不相容,这时 AB = A ,从而 P(AB) = P(A) = p ;由于 AB = A B ,从而 P(AB) = P(A B) =1− P(A B) =1− ( p + q) . 【例 6】某住宅楼共有三个孩子,已知其中至少有一个是女孩,求至少有一个是 男孩的概率(假设一个小孩为男或为女是等可能的). 分析:在已知“至少有一个是女孩”的条件下求“至少有一个是男孩”的概 率,所以是条件概率问题.根据公式 ( ) ( ) ( | ) P A P AB P B A = ,必须求出 P(AB), P(A) . 解:设 A ={至少有一个女孩},B ={至少有一个男孩},则 A ={三个全是男孩}, B ={三个全是女孩},于是 ( ) 8 1 2 1 ( ) 3 P A = = = P B ,事件 AB 为“至少有一个女孩且至少有一个男孩”,因 为 AB = A B ,且 AB = ,所以 P(AB) =1− P(AB) =1− P(A B) = 8 7 , ( ) 1 ( ) 4 3 ) 8 1 8 1 1−[P(A) + P(B)] =1− ( + = P A = − P A = ,从而,在已知至少有 一个为女孩的条件下,求至少有一个是男孩的概率为: 7 6 8 7 4 3 ( ) ( ) ( | ) = = = P A P AB P B A . 【例 7】某电子设备制造厂所用的晶体管是由三家元件制造厂提供的.根据以往的 记录有以下的数据(表 1-1)
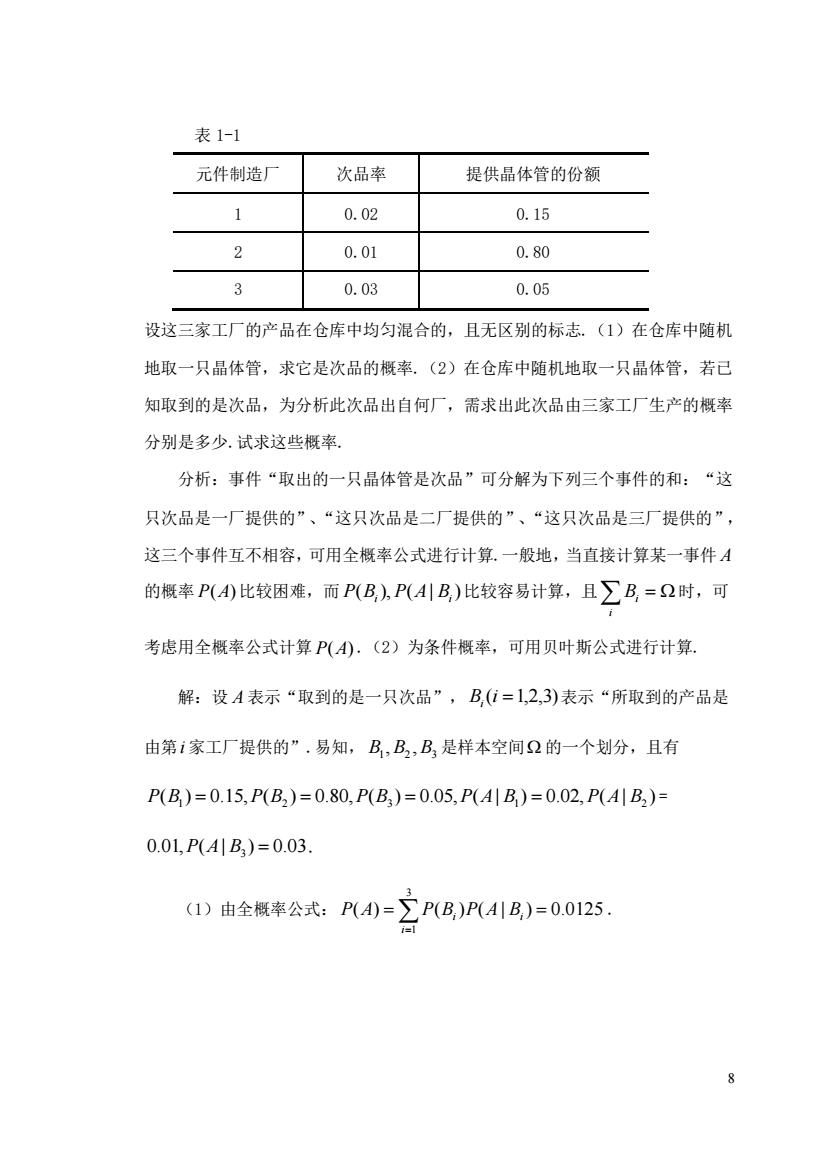
表1-1 元件制造厂 次品率 提供品体管的份额 1 0.02 0.15 2 0.01 0.80 0.03 0.05 设这三家工厂的产品在仓库中均匀混合的,且无区别的标志.(1)在仓库中随机 地取一只品体管,求它是次品的概率.(2)在仓库中随机地取一只品体管,若已 知取到的是次品,为分析此次品出自何厂,需求出此次品由三家工厂生产的概率 分别是多少.试求这些概率 分析:事件“取出的一只晶体管是次品”可分解为下列三个事件的和:“这 只次品是一厂提供的”、“这只次品是二厂提供的”、“这只次品是三厂提供的”, 这三个事件互不相容,可用全概率公式进行计算.一般地,当直接计算某一事件A 的概率P(4)比较困难,而P(B,)P(AB)比较容易计算,且∑B,=2时,可 考虑用全概率公式计算P(A).(2)为条件概率,可用贝叶斯公式进行计算 解:设A表示“取到的是一只次品”,B,(i=1,2,3)表示“所取到的产品是 由第1家工厂提供的”.易知,B,B2,B是样本空间2的一个划分,且有 P(B)=0.15,P(B,)=0.80,P(B,)=0.05,P(A|B)=0.02,P(A|B)= 0.0L,P(AB)=0.03. (I)由全概率公式:P4)=∑P(B,)PAB)=0.0125 8
8 表 1-1 元件制造厂 次品率 提供晶体管的份额 1 0.02 0.15 2 0.01 0.80 3 0.03 0.05 设这三家工厂的产品在仓库中均匀混合的,且无区别的标志.(1)在仓库中随机 地取一只晶体管,求它是次品的概率.(2)在仓库中随机地取一只晶体管,若已 知取到的是次品,为分析此次品出自何厂,需求出此次品由三家工厂生产的概率 分别是多少.试求这些概率. 分析:事件“取出的一只晶体管是次品”可分解为下列三个事件的和:“这 只次品是一厂提供的”、“这只次品是二厂提供的”、“这只次品是三厂提供的”, 这三个事件互不相容,可用全概率公式进行计算.一般地,当直接计算某一事件 A 的概率 P(A) 比较困难,而 ( ), ( | ) P Bi P A Bi 比较容易计算,且 = i Bi 时,可 考虑用全概率公式计算 P(A) .(2)为条件概率,可用贝叶斯公式进行计算. 解:设 A 表示“取到的是一只次品”, B (i =1,2,3) i 表示“所取到的产品是 由第 i 家工厂提供的”.易知, 1 2 3 B ,B ,B 是样本空间 的一个划分,且有 ( ) 0.15, ( ) 0.80, ( ) 0.05, ( | ) 0.02, ( | ) P B1 = P B2 = P B3 = P A B1 = P A B2 = 0.01,P(A| B3 ) = 0.03. (1)由全概率公式: ( ) ( ) ( | ) 0.0125 3 1 = = i= P A P Bi P A Bi

(2)由贝叶斯公式: P代B10=P1IB)B2=024,PA,1A0=064,PB1)=012.以上结 P(A) 果表明,这只次品来自第二家工厂的可能性最大 【例8】一名工人照看A、B、C三台机床,已知在1小时内三台机床各自不需 要工人照看的概率为P(A)=0.9,P(B)=0.8,P(C)=0.7.求1小时内三台机床至 多有一台需要照看的概率. 分析:每台机床是否需要照看是相互独立的,这样,可根据事件的独立性性 质及加法公式进行计算 解:各台机床需要照看的事件是相互独立的,而三台机床至多有一台需要照 看的事件D可写成:D=ABC+ABC+ABC+ABC,则由加法公式与独立性 性质得:P(D)=P(ABC+ABC+ABC+ABC)=P(ABC)H P(ABC)+P(ABC)+P(ABC)=P(A)P(B)P(C)+P(A)P(B)P(C)+ P(A)P(B)P(C)+P(A)P(B)P(C)=0.902. 【例9】某车间有10台同类型的设备,每台设备的电动机功率为10千瓦.己知每 台设备每小时实际开动12分钟,它们的使用是相互独立的.因某种原因,这天供 电部门只能给车间提供50千瓦的电力.问该天这10台设备能正常运作的概率是多 少? 分析:由题意知,所要求的概率就是求“该天同时开动的设备不超过5台” 这一事件的概率.因为每台设备的使用是相互独立的,且在某一时刻,设备只有开
9 (2)由贝叶斯公式: 0.24, ( | ) 0.64, ( | ) 0.12 ( ) ( | ) ( ) ( | ) 2 3 1 1 1 = = P B A = P B A = P A P A B P B P B A .以上结 果表明,这只次品来自第二家工厂的可能性最大. 【例 8】一名工人照看 A、B、C 三台机床,已知在 1 小时内三台机床各自不需 要工人照看的概率为 P(A) = 0.9, P(B) = 0.8, P(C) = 0.7 .求1小时内三台机床至 多有一台需要照看的概率. 分析:每台机床是否需要照看是相互独立的,这样,可根据事件的独立性性 质及加法公式进行计算. 解:各台机床需要照看的事件是相互独立的,而三台机床至多有一台需要照 看的事件 D 可写成: D = ABC + ABC + ABC + ABC ,则由加法公式与独立性 性质得: P(D) = P(ABC + ABC + ABC + ABC) = P(ABC) + P(ABC) + P(ABC) + P(ABC) = P(A)P(B)P(C) + P(A)P(B)P(C) + P(A)P(B)P(C) + P(A)P(B)P(C) =0.902. 【例 9】某车间有 10 台同类型的设备,每台设备的电动机功率为 10 千瓦.已知每 台设备每小时实际开动 12 分钟,它们的使用是相互独立的.因某种原因,这天供 电部门只能给车间提供50千瓦的电力.问该天这10台设备能正常运作的概率是多 少? 分析:由题意知,所要求的概率就是求“该天同时开动的设备不超过 5 台” 这一事件的概率.因为每台设备的使用是相互独立的,且在某一时刻,设备只有开