
§6.4 充分统计量 我们先分析一下上节中导出的罗一克拉美不等式中等号 成立的充要条件(6.26)。 log f(; 日) =K(1-0) L1 a0 其中K不依赖于 51, 2 72 而可能依赖于θ。 对这等式两端求对的积分 log f(;) d0=A(0)n+B(0)+C(51, a 5 2 S 72

或者 1ogL=1ogΠf(x;)=A(⊙)y+B()+C(X1, i-1 X2,…,Xw) (6.43) 这里y=u(区1,X2,…,X)。由此得出,似然函数L (X1,X2,…,X)有形状 Le4(),+B(9)hX1,X2,…, (6.44)

这里h(X1,X2,…,X:)=eCW不依赖于, A(8)和B(8)只是日的函数,所以使罗一克拉美不等式中等 号成立的条件有下列两个: (1)似然还数L能分解成两个因子,即 L(8:X1,…,Xx)=gy;8)h(X1, X2,…,X然) (6.45) 其中第一个因子只依赖于y和B,第二个因子在y值已知时不 依赖于8; (2)第一个因子有指数型分布

A(),+B(8) g(y;0)=e (6.46) 满足条件(1)的统计量称为参数8的充分统计量.满足 条件(2)的门的分布为指数型分布。反过来,如果一个无偏估 计是充分的,且其分布为指数型,那么这个就是一个有效估 计。下面我们将分别研究充分统计量和指数型分布。 在引入充分统计量的概念以前,我们先说明了的直观含 义。 我们知道统计量是子样的函数,它把子样中所含的有关

所研究问题的信息集中起来作为我们进行统计推断的依据。 由于统计量有很多,那么怎样的统计量是最佳的呢?直观的 想法是,一方面要尽可能地简单,另一方面又要能提供子样 所含的“全部信息”。 怎样理解“全部信息”呢?在数理统计学中,子样1, 专2,一,专m给我们提供了母体的信息。如果母体的概 率函数依赖于参数日,子样当然也包含日的信息,但是依赖 于子样的统计量脚不一定包含日的全部信息。例如在一般 情形下,子样的联合概率还数(即似然还数)能分解成

L(8;x1,…,Xx)=gy:8)h(X1,X2,…,Xw) h(X1,X…,Xx;8)是条件门=y下的条件概率函数, 它一般是依赖于8的函数.如果8未知,hX1,X…,x;8) 也就不可能知道,这时统计量门并没有反映子样所含有的“全 部信息”,只有在不依赖于日时,统计量才反映了子样的“全 部信息”。正因为这一点,费歇命名这种反映“全部信息”的 统计量为充分统计量

例6.15(略) 从上面(6.44)式和例6.15看到,1门为8的一个充分统 计量,子样的联合概率函做L应该分解成两个因子,一个因 子与门的概率函数有关,它可以依赖于未知参数日,而另一 个因子应该是条件下子样51,与2,”,。 的条件 概率还数,它与8无关。由此我们引出充分统计量的定义

定义67设51,52,”5m是取自具有概率 函数fc,),日∈⊙的母体的一个容量为n的子样。设 门=以(51,2,”号)是一个统计量,有概率函数 gy,0。若 j,f(,9…fx,0=l818,) (6.47) g[u(1,…,x)]

成立,且每当u(1,…,Xx)取一固定值时,门y发 生条件下的条件概率函数h(X1,…,X:)不依赖于日,则 称门为8的一个充分估计量。 例6.16 设母体专有密度函数 ca=6w”,0<x<o,0eoo 0,其他 和5(1)<5(2)<<5(m)是取自这个母体的子样的 次序统计量
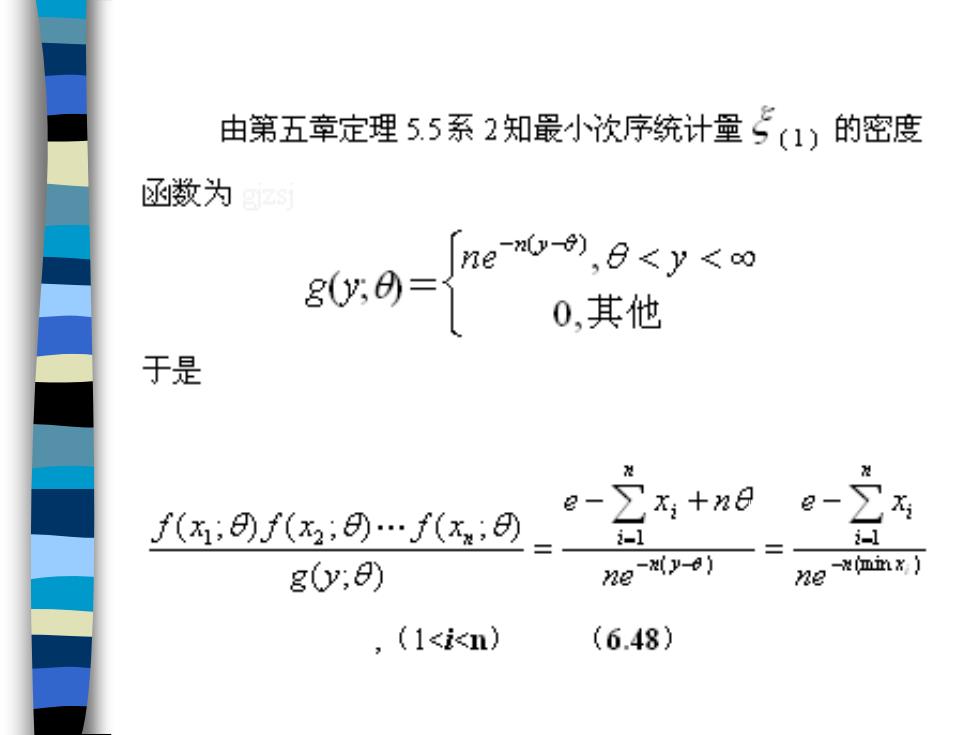
由第五章定理5.5系2知最小次序统计量5(1)的密度 函数为 ne-n-)e<y<oo g0y= 0,其他 于是 -∑x+e f:…f9_g 8- i-1 i-1 g0;) 2e-p) 2e*血若) ,(1<in) (6.48)